17 Rings, Polynomial Rings, Integral Domains, Units

Lecture from: 13.11.2024 | Video: Videos ETHZ

Rings

A ring is an algebraic structure that generalizes the concepts of addition and multiplication from familiar number systems like integers and real numbers. A ring is denoted as $⟨R;+,-,0,\cdot ,1⟩$, where $R$ is a set, $+$ and $\cdot$ are binary operations (addition and multiplication), $-$ is a unary operation (additive inverse), and 0 and 1 are special elements (additive and multiplicative identities).

A ring must satisfy the following properties:

1. Additive Group: $⟨R;+,-,0⟩$ forms an abelian group. This means:

   • Associativity: $(a+b)+c=a+(b+c)$
   • Commutativity: $a+b=b+a$
   • Identity: $a+0=a$
   • Inverse: For every $a$, there exists $-a$ such that $a+(-a)=0$

2. Multiplicative Monoid: $⟨R;\cdot ,1⟩$ forms a monoid. Note that the multiplicative identity $1$ can be equal to $0$ in the trivial ring with just one element. Other rings where $0=1$ do exist too (rings with 0 divisors, we will return to these later), thus 1 is not 0 unless stated. This means:

   • Associativity: $(a\cdot b)\cdot c=a\cdot (b\cdot c)$
   • Identity: $a\cdot 1=1\cdot a=a$

3. Distributivity: Multiplication distributes over addition:

   • Left Distributivity: $a\cdot (b+c)=(a\cdot b)+(a\cdot c)$
   • Right Distributivity: $(a+b)\cdot c=(a\cdot c)+(b\cdot c)$

Applications

Rings have numerous applications in various fields, including:

• Error-Correcting Codes: Rings are used in the construction of error-correcting codes, which are essential for reliable data transmission and storage.

• Secret Sharing: Rings play a role in secret sharing schemes, where a secret is divided into multiple shares distributed among participants, and a certain number of shares are required to reconstruct the secret.

• Privacy Amplification: Rings are used in privacy amplification techniques, where a partially secret shared value (e.g., a bitstring) can be transformed into a shorter, more secret value. A public function $f$ compresses the bitstring (e.g., from 1000 bits to 800 bits). The specific choice of $f$ is public knowledge, but the way it is applied depends on an additional secret. The remaining 200 bits could function like this key, akin to a one-time pad.

Lemmas

• $0\cdot a=0$: $0\cdot a=(0+0)\cdot a=0\cdot a+0\cdot a$. Adding $-(0\cdot a)$ to both sides gives $0=0\cdot a$.

• $(-a)\cdot b=-(a\cdot b)$: $0=0\cdot b=(a+(-a))\cdot b=a\cdot b+(-a)\cdot b$. Adding $-(a\cdot b)$ to both sides gives $-(a\cdot b)=(-a)\cdot b$.

• $1\ne 0$ if $|R|\ge 2$: Proof by contradiction. Assume $1=0$. Let $a\in R$ such that $a\ne 0$ (such an $a$ exists since $|R|\ge 2$). Then $a=a\cdot 1=a\cdot 0=0$, which contradicts our assumption that $a\ne 0$. Therefore, $1\ne 0$.

Gaussian Integers

While familiar rings like $\mathbb{Z}$ (integers) and $\mathbb{R}$ (real numbers) are commonly encountered, let’s explore a different ring: the Gaussian integers.

Gaussian integers are complex numbers of the form $a+bi$, where $a$ and $b$ are integers, and $i$ is the imaginary unit ($i^2=-1$). We can represent Gaussian integers as ordered pairs of integers: $(a,b)$, where $(a,b)$ corresponds to $a+bi$.

The set of Gaussian integers is denoted as $\mathbb{Z}[i]$. We define the ring operations as follows:

• Addition: $(a,b)+(a^{\prime },b^{\prime })=(a+a^{\prime },b+b^{\prime })$. This corresponds to the usual addition of complex numbers: $(a+bi)+(a^{\prime }+b^{\prime }i)=(a+a^{\prime })+(b+b^{\prime })i$.

• Multiplication: $(a,b)\cdot (a^{\prime },b^{\prime })=(a{a}^{\prime }-b{b}^{\prime },a{b}^{\prime }+b{a}^{\prime })$. This corresponds to the multiplication of complex numbers: $(a+bi)\cdot (a^{\prime }+b^{\prime }i)=(a{a}^{\prime }-b{b}^{\prime })+(a{b}^{\prime }+b{a}^{\prime })i$.

• Additive Identity: The additive identity is $(0,0)$, corresponding to $0+0i=0$.

• Multiplicative Identity: The multiplicative identity is $(1,0)$, corresponding to $1+0i=1$. This is because $(a,b)\cdot (1,0)=(a\cdot 1-b\cdot 0,a\cdot 0+b\cdot 1)=(a,b)$.

• Additive Inverse: The additive inverse of $(a,b)$ is $(-a,-b)$, corresponding to $-(a+bi)=-a-bi$.

The Gaussian integers form a ring, $⟨\mathbb{Z}[i];+,-,(0,0),\cdot ,(1,0)⟩$, because they satisfy all the ring axioms (additive group, multiplicative monoid, and distributivity). These properties are inherited from the complex numbers.

Visualization:

Gaussian integers can be visualized as points on a two-dimensional grid (complex plane), where the horizontal axis represents the real part ($a$) and the vertical axis represents the imaginary part ($b$). Addition corresponds to vector addition on this grid. Multiplication has a geometric interpretation involving rotation and scaling, which is a bit more complex to visualize directly on the grid.

Divisibility in Gaussian Integers (Clicker…)

Divisibility in Gaussian Integers

In the ring of Gaussian integers, $\mathbb{Z}[i]$, we say that a Gaussian integer $a$ divides another Gaussian integer $b$ (denoted as $a|b$) if there exists a Gaussian integer $c$ such that $b=a\cdot c$.

How to determine if $a|b$:

Divisibility in Gaussian integers is slightly more nuanced than in regular integers. We use the concept of the norm of a Gaussian integer. The norm of $z=a+bi$, denoted as $N(z)$ or $|z{|}^2$, is defined as $N(z)=a^2+b^2$. The norm is always a non-negative integer.

1. Calculate the norms: Compute $N(a)$ and $N(b)$.

2. Check integer divisibility: If $a|b$, then $N(a)$ must divide $N(b)$ in the regular integers. This is a necessary condition, but not sufficient. If $N(a)$ does not divide $N(b)$, then $a$ cannot divide $b$.

3. Complex division: If $N(a)$ divides $N(b)$, perform the complex division $\frac{b}{a}=\frac{b\cdot \bar{a}}{N(a)}$, where $\bar{a}$ is the complex conjugate of $a$ (if $a=x+yi$, then $\bar{a}=x-yi$).

4. Check if the quotient is a Gaussian integer: If the real and imaginary parts of the resulting quotient are both integers, then $a|b$. Otherwise, $a$ does not divide $b$.

Examples:

1. Does $(1+i)$ divide $(2)$?
   • $N(1+i)=1^2+1^2=2$
   • $N(2)=2^2+0^2=4$
   • $2$ divides $4$, so we proceed to complex division: $\frac{2}{1+i}=\frac{2(1-i)}{2}=1-i$.
   • Since $1-i$ is a Gaussian integer, $(1+i)|(2)$.
2. Does $(1+i)$ divide $(3)$?
   • $N(1+i)=2$
   • $N(3)=9$
   • $2$ does not divide $9$, so $(1+i)$ does not divide $(3)$.
3. Does $(2+i)$ divide $(4+7i)$?
   • $N(2+i)=5$
   • $N(4+7i)=16+49=65$
   • $5$ divides $65$, so we perform complex division: $\frac{4+7i}{2+i}=\frac{(4+7i)(2-i)}{5}=\frac{8-4i+14i-7i^2}{5}=\frac{15+10i}{5}=3+2i$.
   • Since $3+2i$ is a Gaussian integer, $(2+i)|(4+7i)$.
4. Does $(2)$ divide $(1+i)$?
   • $N(2)=4$
   • $N(1+i)=2$
   • $4$ does not divide $2$, hence $2$ does not divide $1+i$.

By using the norm and performing complex division, we can systematically determine divisibility in the ring of Gaussian integers.

Greatest Common Divisor (GCD) of Gaussian Integers

Units in Gaussian Integers

A unit in a ring is an element that has a multiplicative inverse within the ring. In other words, an element $u$ is a unit if there exists an element $v$ in the ring such that $u\cdot v=v\cdot u=1$.

In the ring of Gaussian integers, $\mathbb{Z}[i]$, we can find the units using the norm. If $u=a+bi$ is a unit, then there exists $v=c+di$ such that $u\cdot v=1$. Taking the norm of both sides, we get $N(u\cdot v)=N(1)$, which implies $N(u)N(v)=1$. Since the norm of a Gaussian integer is always a non-negative integer, we must have $N(u)=1$.

So, we need to find Gaussian integers $a+bi$ such that $a^2+b^2=1$. The integer solutions to this equation are:

• $a=1,b=0⟹u=1$
• $a=-1,b=0⟹u=-1$
• $a=0,b=1⟹u=i$
• $a=0,b=-1⟹u=-i$

See the yellow dots…

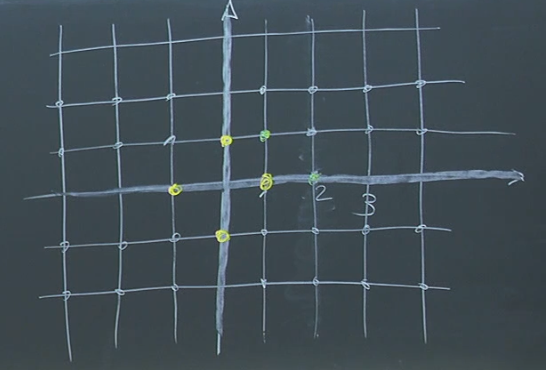
Therefore, the units in $\mathbb{Z}[i]$ are $1,-1,i,$ and $-i$. These are the only Gaussian integers that have multiplicative inverses within $\mathbb{Z}[i]$.

For future reference, when we discuss error-correcting codes, we will encounter a similar structure involving tuples of 8 bits. In this context, the underlying ring will be ${\mathbb{Z}}_2^8$, representing byte-sized sequences where each element within the tuple is an element of ${\mathbb{Z}}_2$.

Polynomial Rings: $R[x]$

Beyond numbers, rings can also be constructed using polynomials. Given a ring $R$, we can form the polynomial ring $R[x]$, where the coefficients of the polynomials are elements of $R$.

Elements of $R[x]$ are polynomials of the form $a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n$, where $a_i\in R$ are the coefficients and $x$ is the indeterminate (or variable). We can represent these polynomials as sequences of their coefficients: $(a_0,a_1,a_2,\dots ,a_n,0,0,\dots )$, where only a finite number of coefficients are non-zero. For instance, if $R={\mathbb{Z}}_2$, the polynomial $1+x+x^2$ would be represented as $(1,1,1,0,0,\dots )$.

The ring operations are defined as follows:

• Addition: Addition is component-wise, using the addition operation of $R$. If $a(x)=(a_0,a_1,a_2,\dots )$ and $b(x)=(b_0,b_1,b_2,\dots )$, then $a(x)+b(x)=(a_0+b_0,a_1+b_1,a_2+b_2,\dots )$, where each $a_i+b_i$ is performed in $R$.

• Multiplication: Multiplication is defined using the distributive law and the rule $x^i\cdot x^j=x^{i+j}$. The product of two polynomials $a(x)$ and $b(x)$ is given by the convolution of their coefficient sequences, with coefficient operations performed in $R$: $a(x)\cdot b(x)=(c_0,c_1,c_2,\dots )$, where $c_k={\sum }_{i+j=k}{a}_i{b}_j$. For example, if $a(x)=(a_0,a_1,a_2)$ and $b(x)=(b_0,b_1,b_2,b_3)$, then the coefficients of the product are:

  • $c_0=a_0{b}_0$
  • $c_1=a_0{b}_1+a_1{b}_0$
  • $c_2=a_0{b}_2+a_1{b}_1+a_2{b}_0$
  • $c_3=a_0{b}_3+a_1{b}_2+a_2{b}_1$
  • $c_4=a_1{b}_3+a_2{b}_2$
  • $c_5=a_2{b}_3$
  • $c_k=0$ for $k>5$ All these coefficient operations are performed using the multiplication and addition defined in $R$.

• Additive Identity: The additive identity is the zero polynomial, represented by the sequence $(0,0,0,\dots )$, where $0$ is the additive identity in $R$.

• Multiplicative Identity: The multiplicative identity is the constant polynomial 1, represented by the sequence $(1,0,0,\dots )$, where $1$ is the multiplicative identity in $R$.

• Additive Inverse: The additive inverse of $(a_0,a_1,a_2,\dots )$ is $(-a_0,-a_1,-a_2,\dots )$, where $-a_i$ is the additive inverse of $a_i$ in $R$.

$R[x]$ forms a ring under these operations. The familiar ring $\mathbb{Z}[x]$ is a specific instance of this construction where $R=\mathbb{Z}$.

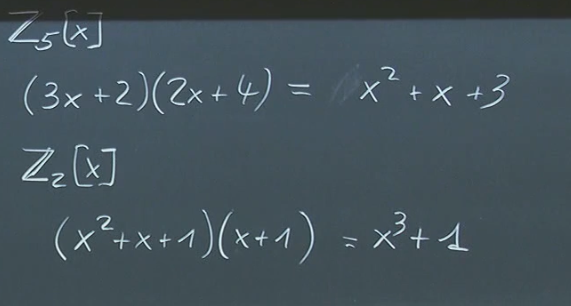
Units in Polynomial Rings

A unit in a ring $R$ is an element that has a multiplicative inverse within the ring. In other words, an element $a\in R$ is a unit if there exists an element $b\in R$ such that $a\cdot b=b\cdot a=1$, where 1 is the multiplicative identity of $R$. The set of all units in $R$ is denoted by $R^{\ast }$. This $R^{\ast }$ forms a group by itself under the multiplication operation of $R$.

In the case of polynomial rings, determining the units depends on the underlying ring $R$.

• If $R$ is a field: If $R$ is a field (we’ll look at this later) (like $\mathbb{R}$ or $\mathbb{Q}$), then the units in $R[x]$ are precisely the non-zero constant polynomials. This is because the degree of the product of two polynomials is the sum of their degrees. Therefore, for a polynomial to have an inverse, its degree must be zero (a constant). Only constant polynomials that are themselves units in $R$ will be units in the polynomial ring, however since we assumed $R$ is a field, all elements (except 0) must be units.

• If $R$ is not a field: If $R$ is not a field (like $\mathbb{Z}$), then the units in $R[x]$ are the polynomials whose constant term is a unit in $R$ and all other coefficients are nilpotent (meaning some power of the coefficient is zero) in $R$. In the simpler case of $\mathbb{Z}[x]$, the units are only the constant polynomials 1 and -1, because these are the only units in $\mathbb{Z}$.

For example, in $\mathbb{Z}[x]$, the polynomial $2x+1$ is not a unit because there is no polynomial in $\mathbb{Z}[x]$ that, when multiplied by $2x+1$, yields 1. However, in $\mathbb{R}[x]$, $2x+1$ is a unit because its inverse within $\mathbb{R}[x]$ is $(2x+1{)}^{-1}=\frac{1}{2x+1}$.

Example: Graded Exercise from Last Exam - Commutativity of Addition in a Ring

While the standard definition of a ring requires the additive group $⟨R;+,-,0⟩$ to be abelian (commutative), we can demonstrate that commutativity of addition follows from the other ring axioms, even without explicitly requiring it.

Proof:

We want to show that for any $a,b\in R$, $a+b=b+a$. We’ll use distributivity, the properties of the additive identity (0), and the multiplicative identity (1).

1. Expand (1 + 1)(a + b) using right distributivity: $(1+1)(a+b)=(1+1)a+(1+1)b$

2. Expand the terms using left distributivity: $(1+1)a+(1+1)b=(1a+1a)+(1b+1b)$

3. Simplify using the multiplicative identity property (1a = a and 1b = b): $(1a+1a)+(1b+1b)=(a+a)+(b+b)$

4. Now expand (1 + 1)(a + b) using left distributivity first: $(1+1)(a+b)=1(a+b)+1(a+b)$

5. Simplify using the multiplicative identity property: $1(a+b)+1(a+b)=(a+b)+(a+b)$

6. We now have two expressions for (1 + 1)(a + b): $(a+a)+(b+b)=(a+b)+(a+b)$

7. Add -a to the left of both sides (using associativity and the additive inverse property): $-a+[(a+a)+(b+b)]=-a+[(a+b)+(a+b)]$ $(-a+a)+(a+(b+b))=(-a+a)+(b+(a+b))$ $0+(a+(b+b))=0+(b+(a+b))$ $a+(b+b)=b+(a+b)$

8. Add -b to the right of both sides (using associativity and additive inverses): $(a+(b+b))+(-b)=(b+(a+b))+(-b)$ $a+((b+b)+(-b))=b+((a+b)+(-b))$ $a+(b+(b+(-b)))=b+(a+(b+(-b)))$ $a+(b+0)=b+(a+0)$ $a+b=b+a$

Therefore, we have proven that addition is commutative in a ring, even without explicitly including it as an axiom.

Irreducible Elements

In a ring, an irreducible element is analogous to a prime number in the integers. An element $p$ of a ring $R$ is called irreducible if it satisfies the following conditions:

1. Non-zero and Non-unit: $p$ is not zero and not a unit (i.e., it does not have a multiplicative inverse in $R$).
2. If $p=ab$, then either $a$ or $b$ is a unit. This means $p$ cannot be factored into two non-unit elements.

Essentially, irreducible elements are those that cannot be “broken down” further into smaller non-trivial factors within the ring.

Examples:

1. Gaussian Integers ($\mathbb{Z}[i]$):

• $1+i$ is irreducible: Suppose $1+i=(a+bi)(c+di)$. Taking the norm (magnitude squared) of both sides, we get $2=(a^2+b^2)(c^2+d^2)$. Since $a,b,c,d$ are integers, the only possible factorizations of 2 are $2=1\cdot 2$ or $2=2\cdot 1$. This implies that either $a^2+b^2=1$ or $c^2+d^2=1$. If $a^2+b^2=1$, then $a+bi$ is a unit in $\mathbb{Z}[i]$ (e.g., $1,-1,i,-i$). Similarly, if $c^2+d^2=1$, then $c+di$ is a unit. Therefore, $1+i$ is irreducible.
• 3 is irreducible: Suppose $3=(a+bi)(c+di)$. Taking the norm gives $9=(a^2+b^2)(c^2+d^2)$. The possible factorizations of 9 are $9=1\cdot 9=9\cdot 1=3\cdot 3$. If $a^2+b^2=1$ or $9$, then as before, we get units when they equal to $1$ and non-unit when they equal $9$. The interesting case is $3=3$. We are looking for a,b integers s.t. $a^2+b^2=3$. However, this equation has no integer solutions. Therefore, 3 is irreducible in $\mathbb{Z}[i]$.
• 5 is not irreducible: $5=(1+2i)(1-2i)$, and neither $1+2i$ nor $1-2i$ are units (their norms are 5, not 1).

2. ${\mathbb{Z}}_2[x]$:

• $x$ is irreducible: If $x=p(x)q(x)$, then one of $p(x)$ or $q(x)$ must have degree 0 (be a constant). Since the only units in ${\mathbb{Z}}_2[x]$ are the non-zero constant polynomials (which are just 1 in this case), either $p(x)$ or $q(x)$ must be 1, making $x$ irreducible.
• $1+x$ is irreducible: Similar to the case of $x$, if $1+x=p(x)q(x)$, one of the factors must be a constant (and therefore a unit).
• $x^4+x^2+1$ is not irreducible in ${\mathbb{Z}}_2[x]$: This factors to $(x^2+x+1{)}^2$ in ${\mathbb{Z}}_2[x]$.

Integral Domains and Zero Divisors

An integral domain is a commutative ring with a multiplicative identity ($1\ne 0$) and no zero divisors.

Zero Divisors: A zero divisor is a non-zero element $a$ of a ring $R$ such that there exists a non-zero element $b\in R$ with $a\cdot b=0$. In other words, zero divisors are non-zero elements that, when multiplied by another non-zero element, produce zero.

Example in ${\mathbb{Z}}_{20}$:

In the ring ${\mathbb{Z}}_{20}$ (integers modulo 20), consider the elements 8 and 15. Both are non-zero. However, $8{\cdot }_{20}15=120\equiv 0(\mathrm{mod}20)$. Therefore, both 8 and 15 are zero divisors in ${\mathbb{Z}}_{20}$.

Avoiding Zero Divisors:

The presence of zero divisors can lead to complications when performing arithmetic operations, such as losing the cancellation property. For example, in ${\mathbb{Z}}_{20}$, $8\cdot 15=0$, but this doesn’t imply that either 8 or 15 are equal to 0. This is why integral domains, which have no zero divisors, are often preferred for many applications. A key property of integral domains is the cancellation property: if $ab=ac$ and $a\ne 0$, then $b=c$.

Units and the Group of Units ($R^{\ast }$)

Within a ring $R$, a unit is an element that has a multiplicative inverse within the ring. Formally, an element $a\in R$ is a unit if there exists an element $b\in R$ such that $a\cdot b=b\cdot a=1$. The set of all units in a ring $R$ is denoted by $R^{\ast }$.

$R^{\ast }$ forms a group under the ring’s multiplication operation. This group is called the group of units of the ring $R$. Let’s verify the group properties:

1. Closure: If $a$ and $b$ are units in $R$, then there exist $a^{-1}$ and $b^{-1}$ in $R$. The product $ab$ also has an inverse in $R$, namely $b^{-1}{a}^{-1}$, since $(ab)(b^{-1}{a}^{-1})=a(b{b}^{-1})a^{-1}=a1a^{-1}=a{a}^{-1}=1$. Therefore, $ab\in R^{\ast }$.
2. Associativity: The associativity of multiplication is inherited from the ring $R$.
3. Identity: The multiplicative identity 1 of the ring $R$ serves as the identity element of the group $R^{\ast }$, since $1\cdot a=a\cdot 1=a$ for any $a\in R^{\ast }$.
4. Inverses: By definition, every element $a$ in $R^{\ast }$ has a multiplicative inverse $a^{-1}$ in $R^{\ast }$.

Examples:

• Integers ($\mathbb{Z}$): The units in $\mathbb{Z}$ are 1 and -1, so ${\mathbb{Z}}^{\ast }=\{1,-1\}$.
• Real Numbers ($\mathbb{R}$): The units in $\mathbb{R}$ are all non-zero real numbers, so ${\mathbb{R}}^{\ast }=\mathbb{R}\setminus \{0\}$.
• Gaussian Integers ($\mathbb{Z}[i]$): The units in $\mathbb{Z}[i]$ are $1,-1,i,-i$. These are the only Gaussian integers with a norm (magnitude squared) equal to 1.
• ${\mathbb{Z}}_n$: The units of ${\mathbb{Z}}_n$ are $a$, where $\text{gcd}(a,n)=1$. Therefore $|{\mathbb{Z}}_n^{\ast }|=\varphi (n)$. (See [[16 Isomorphism, Powers, Order, Generators, Lagrange’s Theorem, Multiplicative Groups, Euler’s Totient Function, RSA#eulers-totient-function—phim|Euler’s Totient Function $phi(m)$]])