Chapter 3 - Sets, Relations, and Functions

3.1 Introduction

TLDR: This chapter introduces set theory, starting with an intuitive understanding of sets as collections of objects. However, it immediately highlights the limitations of a naive approach to set theory by presenting Russell’s paradox, which demonstrates the need for a more rigorous axiomatic foundation.

3.1.1 An Intuitive Understanding of Sets

Definition (Informal):

A set is a well-defined collection of distinct objects. These objects are called the elements or members of the set. We use curly braces {} to denote sets.

Examples:

• Example 3.1: The set of all even numbers: $\{2,4,6,8,...\}$. Note: This is an infinite set, represented using an ellipsis to suggest continuation of the pattern.

• Example 3.1: The set of vowels in the English alphabet: $\{a,e,i,o,u\}$. This is a finite set.

• Example 3.1: The set of prime numbers less than 10: $\{2,3,5,7\}$. This is also a finite set.

• Notation: $x\in A$ means that $x$ is an element of set $A$. $x\notin A$ means that $x$ is not an element of $A$.

Set Cardinality (Informal):

The cardinality of a finite set is the number of elements it contains. We denote it as $|A|$.

Examples:

• Example 3.1: $|\{a,e,i,o,u\}|=5$
• Example 3.1: $|\{2,3,5,7\}|=4$

3.1.2 Russell’s Paradox

Russell’s paradox demonstrates the inconsistency of naive set theory, where any definable collection of objects is considered a set. This paradox highlights the need for a more rigorous axiomatic approach.

The Paradox:

Consider the set $R$ defined as:

$R=\{x|x\notin x\}$.

This attempts to define R as the set of all sets that do not contain themselves as members. Let’s analyze this:

1. Case 1: $R\in R$ If R is a member of itself, then by the definition of R, it must not be a member of itself, which is a contradiction.

2. Case 2: $R\notin R$ If R is not a member of itself, then by the definition of R, it should be a member of itself, which is another contradiction.

Resolution:

This contradiction arises from the unrestricted definition of sets. The naive set theory assumes that any property can be used to define a set. Russell’s paradox shows this assumption is false. It illustrates the need for a formal axiomatic system for set theory (e.g., Zermelo-Fraenkel set theory) that prevents the construction of self-contradictory sets like R. Axiomatic set theory carefully restricts how sets are defined, avoiding such paradoxes.

Additional Examples and Considerations:

• Example illustrating the need for well-defined sets: The collection of “all large numbers” is not a well-defined set. “Large” is subjective and does not create a definite boundary that determines which numbers are and aren’t included. A precise definition of the property that defines the collection is needed to create a well-defined set.

• The importance of axioms in set theory: Axiomatic set theories (like Zermelo-Fraenkel set theory or von Neumann-Bernays-Gödel set theory) lay down specific rules for creating sets. These axioms prevent the creation of contradictory sets like Russell’s R and provide a solid foundation for the study of sets.

3.2 Sets and Operations on Sets

TLDR: This chapter introduces sets as unordered collections of unique elements, defines set equality, and explores fundamental set operations (union, intersection, difference, power set, Cartesian product). It also shows how to construct the natural numbers from the empty set and the successor operation.

3.2.1 The Set Concept

A set is an unordered collection of distinct objects. We represent sets using curly braces {}. The objects within a set are called its elements. Order and repetition of elements are irrelevant.

Example 3.1:

The set of prime numbers less than 10 is $\{2,3,5,7\}$. The set $\{2,7,3,5\}$ represents the same set. The set $\{2,2,3,5,7\}$ also represents the same set (repeated elements are ignored).

3.2.2 Set Equality and Constructing Sets From Sets

Set Equality:

Two sets, A and B, are equal ($A=B$) if and only if they contain exactly the same elements. This is the axiom of extensionality. The manner in which the sets are described is irrelevant.

Constructing Sets from Sets:

We can create new sets from existing ones. This is an important process and foundational to set theory.

Examples:

• We can create a singleton set, which is a set containing only one element: $\{a\}$.
• We can create sets with multiple elements: $\{a,b,c\}$.

3.2.3 Subsets

Definition:

A set $A$ is a subset of a set $B$ ($A\subseteq B$) if every element of $A$ is also an element of $B$. $A$ is a proper subset of $B$ ($A\subset B$) if $A\subseteq B$ and $A\ne B$.

Example 3.3:

$\{2,3\}\subseteq \{2,3,5,7\}$. $\{2,3\}$ is a subset of $\{2,3,5,7\}$. $\{2,3,5,7\}\subseteq \{2,3,5,7\}$ is also true, but not a proper subset. $\{2,3,5\}\subset \{2,3,5,7\}$ because every element of $\{2,3,5\}$ is in $\{2,3,5,7\}$, and the sets are not identical.

3.2.4 Union and Intersection

Definitions:

• Union ($\cup$): The union of sets $A$ and $B$, denoted $A\cup B$, is the set containing all elements found in either $A$ or $B$ (or both): $A\cup B=\{x|x\in A\vee x\in B\}$.

• Intersection ($\cap$): The intersection of sets $A$ and $B$, denoted $A\cap B$, is the set containing only the elements common to both $A$ and $B$: $A\cap B=\{x|x\in A\wedge x\in B\}$.

Examples:

• Example 3.2: Let $A=\{a,b,c\}$ and $B=\{b,c,d\}$. Then $A\cup B=\{a,b,c,d\}$ and $A\cap B=\{b,c\}$.

3.2.5 The Empty Set

Definition:

The empty set, denoted $\varnothing$ or $\{\}$, is the unique set containing no elements. For any element $x$, $x\notin \varnothing$.

Lemma 3.5:

There is only one empty set.

Proof: (Indirect) Assume there are two distinct empty sets, ${\varnothing }_1$ and ${\varnothing }_2$. By the definition of an empty set, ${\varnothing }_1$ and ${\varnothing }_2$ contain no elements. Since they have the same elements (none), ${\varnothing }_1={\varnothing }_2$ by the axiom of extensionality. This contradiction shows that only one empty set can exist.

Lemma 3.6:

The empty set is a subset of every set: $\forall A(\varnothing \subseteq A)$.

Proof: (Indirect) Suppose there exists a set $A$ such that $\varnothing ⊈A$. This implies there is at least one element $x$ such that $x\in \varnothing$ and $x\notin A$. However, by the definition of the empty set, there are no such elements $x$. This contradiction proves that the empty set is a subset of every set.

More rigorously:

3.2.6 Constructing Sets from the Empty Set

The empty set is a foundational concept. Using only set-theoretic operations, we can build any set starting with the empty set. This is often demonstrated through the construction of the natural numbers (see below).

3.2.7 A Construction of the Natural Numbers

The natural numbers can be constructed recursively from the empty set using the successor function.

Definitions:

• Zero (0): Defined as the empty set, $\varnothing$.
• Successor Function (s): For a set $x$, its successor is $s(x)=x\cup \{x\}$.

Construction:

1. $0=\varnothing$
2. $1=s(0)=0\cup \{0\}=\varnothing \cup \{\varnothing \}=\{\varnothing \}$
3. $2=s(1)=1\cup \{1\}=\{\varnothing \}\cup \{\{\varnothing \}\}=\{\varnothing ,\{\varnothing \}\}$
4. $3=s(2)=2\cup \{2\}=\{\varnothing ,\{\varnothing \},\{\varnothing ,\{\varnothing \}\}\}$ …and so on.

Each natural number is defined as a set containing all previous numbers in the sequence. The cardinality of each set corresponds to the number it represents.

3.2.8 The Power Set of a Set

Definition:

The power set of a set $A$, denoted $P(A)$ or $2^A$, is the set of all subsets of $A$: $P(A)=\{B|B\subseteq A\}$.

Example 3.5:

If $A=\{a,b\}$, then $P(A)=\{\varnothing ,\{a\},\{b\},\{a,b\}\}$. Note that $|P(A)|=2^{|A|}$, where $|A|$ denotes the cardinality of A.

3.2.9 The Cartesian Product of Sets

Definition:

The Cartesian product of sets $A$ and $B$, denoted $A\times B$, is the set of all possible ordered pairs $(a,b)$ where $a\in A$ and $b\in B$: $A\times B=\{(a,b)|a\in A\wedge b\in B\}$.

Example 3.7:

If $A=\{a,b\}$ and $B=\{c,d\}$, then $A\times B=\{(a,c),(a,d),(b,c),(b,d)\}$. Note that the order matters in ordered pairs: $(a,b)\ne (b,a)$ unless $a=b$. Also, $|A\times B|=|A|\times |B|$.

3.3 Relations

TLDR: This chapter defines relations as sets of ordered pairs and explores various ways to represent and manipulate them. It introduces fundamental operations on relations (union, intersection, inverse, composition) and examines key properties (reflexive, symmetric, transitive), culminating in the concept of transitive closure. Equivalence relations, a special type of relation possessing all three properties are discussed as well.

3.3.1 The Relation Concept

Definition:

A relation $R$ from a set $A$ (the domain) to a set $B$ (the codomain) is a subset of the Cartesian product $A\times B$, i.e., $R\subseteq A\times B$. Each element of $R$ is an ordered pair $(a,b)$ where $a\in A$ and $b\in B$. If $A=B$, $R$ is a relation on $A$. We write $aRb$ to denote $(a,b)\in R$.

Examples:

• Example 3.8: Let $S$ be a set of students and $C$ be a set of courses. The relation “takes” where $(s,c)\in takes$ if student $s$ is taking course $c$.

• Example 3.9: On the set of all people, we can define relations like “parent of,” “child of,” “sibling of,” “married to,” etc. Each such relation is a subset of (People × People).

• Example 3.10: On the set of integers, we have relations like $=$, $\ne$, $<$, $>$, $\le$, $\ge$, $|$ (divides), $\nmid$ (does not divide). Each of these is a subset of (Integers × Integers).

• Example 3.11: The relation ${\equiv }_m$ (congruence modulo m) on the integers, where $a{\equiv }_{m}b$ if $a$ and $b$ have the same remainder when divided by $m$. This relation is defined as ${\equiv }_m=\{(a,b)\mid \exists k(a-b=km)\}$.

• Example 3.12: The relation $\{(x,y)\mid x^2+y^2=1\}$ on the set of real numbers $\mathbb{R}$ represents the set of points on the unit circle (a subset of $\mathbb{R}\times \mathbb{R}$).

• Example 3.13: For any set $S$, the subset relation $\subseteq$ is a relation on the power set $\mathcal{P}(S)$ (the set of all subsets of $S$).

3.3.2 Representations of Relations

Relations can be represented in several ways:

1. List of Ordered Pairs: Explicitly listing all the ordered pairs in the relation (Example 3.12).

2. Diagram: A visual representation using nodes representing elements from the domain and codomain, with arrows (directed edges) to show the relation. Useful for small sets.

3. Matrix: A Boolean matrix where the rows and columns correspond to elements of the domain and codomain, respectively. A 1 in row $i$ and column $j$ indicates that the pair ($i$, $j$) is in the relation, and 0 indicates that it is not. This is especially useful for finite sets.

Examples:

Let $A=\{a,b,c\}$ and $B=\{1,2,3\}$.

• Example 3.15: For the relation $R=\{(a,1),(a,2),(b,3),(c,1),(c,3)\}$, the matrix representation is:

R 1 2 3
a 1 1 0
b 0 0 1
c 1 0 1

3.3.3 Set Operations on Relations

Since relations are sets, we can apply standard set operations:

1. Union ($\cup$): $R\cup S=\{(a,b)\mid (a,b)\in R\vee (a,b)\in S\}$. The union of two relations contains all pairs from either relation.

2. Intersection ($\cap$): $R\cap S=\{(a,b)\mid (a,b)\in R\wedge (a,b)\in S\}$. The intersection contains only pairs common to both relations.

3. Complement ($\overline{R}$): $\overline{R}=(A\times B)\setminus R$. The complement contains all pairs in $A\times B$ that are not in $R$.

3.3.4 The Inverse of a Relation

Definition:

The inverse of a relation $R$, denoted $R^{-1}$ or $\hat{R}$, is obtained by swapping the elements in each ordered pair. Formally, $R^{-1}=\{(b,a)\mid (a,b)\in R\}$.

Examples:

• Example 3.19: If $R$ is the “owns” relation from the set of people to the set of objects, then $R^{-1}$ is the “is owned by” relation.

• Example 3.20: If $R$ is the “parent of” relation, $R^{-1}$ is the “child of” relation.

• Example 3.21: The inverse of the relation $<$ on integers is the relation $>$.

3.3.5 Composition of Relations

Definition:

Let $R$ be a relation from $A$ to $B$, and $S$ a relation from $B$ to $C$. The composition of $R$ and $S$, denoted $R\circ S$, is the relation from $A$ to $C$ such that $a(R\circ S)c$ if and only if there exists some $b\in B$ such that $aRb$ and $bSc$. Formally, $R\circ S=\{(a,c)\mid \exists b\in B((a,b)\in R\wedge (b,c)\in S)\}$.

Lemma 3.7 (Associativity of Relation Composition):

$(R\circ S)\circ T=R\circ (S\circ T)$. The composition of relations is associative.

Proof:

We need to show that $\forall a,c((a,c)\in (R\circ S)\circ T\iff (a,c)\in R\circ (S\circ T))$. Let’s consider one direction:

Assume $(a,c)\in (R\circ S)\circ T$. Then $\exists b((a,b)\in (R\circ S)\wedge (b,c)\in T)$. This means $\exists b(\exists d((a,d)\in R\wedge (d,b)\in S)\wedge (b,c)\in T)$. Thus $\exists b\exists d((a,d)\in R\wedge (d,b)\in S\wedge (b,c)\in T)$. But this means $\exists d((a,d)\in R\wedge \exists b((d,b)\in S\wedge (b,c)\in T))$. This implies $\exists d((a,d)\in R\wedge (d,c)\in (S\circ T))$, which means $(a,c)\in R\circ (S\circ T)$. The opposite direction is shown similarly.

3.3.6 Special Properties of Relations

Relations can have several special properties that define important classes of relations:

1. Reflexive:

A relation $R$ on a set $A$ is reflexive if every element is related to itself: $\forall a\in A(aRa)$. This means that the identity relation $I_A=\{(a,a)\mid a\in A\}\subseteq R$.

Examples:

• The relation “equals” ($=$) is reflexive.
• The relation "$\le$" (less than or equal to) is reflexive.
• The relation "$\ge$" is reflexive.
• The relation “divides” on integers is reflexive.

2. Symmetric:

A relation $R$ on $A$ is symmetric if whenever $a$ is related to $b$, then $b$ is also related to $a$: $\forall a,b\in A(aRb\Rightarrow bRa)$.

Examples:

• The relation “equals” ($=$) is symmetric.
• The relation “is a sibling of” is symmetric.
• The relation “is married to” is symmetric.
• The relation "${\equiv }_m$" (congruence modulo m) is symmetric.

3. Transitive:

A relation $R$ on $A$ is transitive if whenever $a$ is related to $b$ and $b$ is related to $c$, then $a$ is related to $c$: $\forall a,b,c\in A((aRb\wedge bRc)\Rightarrow aRc)$.

Examples:

• The relation “equals” ($=$) is transitive.
• The relation "$\le$" (less than or equal to) is transitive.
• The relation "$\ge$" is transitive.
• The relation “is an ancestor of” is transitive.
• The relation “divides” on integers is transitive.
• The relation "${\equiv }_m$" (congruence modulo $m$) is transitive.

4. Antisymmetric:

A relation $R$ on $A$ is antisymmetric if whenever $a$ is related to $b$ and $b$ is related to $a$, then $a$ and $b$ are the same element: $\forall a,b\in A((aRb\wedge bRa)\Rightarrow a=b)$. Note that this does not mean that the relation is not symmetric.

Examples:

• The relation "$\le$" (less than or equal to) is antisymmetric.
• The relation "$\ge$" is antisymmetric.
• The relation “is a subset of” ($\subseteq$) is antisymmetric.
• The relation “divides” on positive integers is antisymmetric. (If a divides b and b divides a, then a = b).

5. Asymmetric:

A relation $R$ on $A$ is asymmetric if whenever $a$ is related to $b$, then $b$ is not related to $a$: $\forall a,b\in A(aRb\Rightarrow \neg bRa)$. Note that this is different from “not symmetric”. A relation can be neither symmetric nor asymmetric.

Examples:

• The relation $<$ (strictly less than) on integers is asymmetric.
• The relation $>$ (strictly greater than) on integers is asymmetric.
• The relation “is a parent of” is asymmetric (generally ; we assume that there are no instances of an individual being their own parent).

3.3.7 Transitive Closure

Definition:

The transitive closure $R^{\ast }$ of a relation $R$ on a set $A$ is the smallest transitive relation containing $R$. It’s essentially all pairs $(a,c)$ such that there exists a sequence $a,b_1,b_2,...,b_n,c$ where each consecutive pair is in $R$.

Example:

Consider the relation $R=\{(1,2),(2,3),(3,4)\}$. The transitive closure is $R^{\ast }=\{(1,2),(2,3),(3,4),(1,3),(2,4),(1,4)\}$.

3.4 Equivalence Relations

TLDR: This section defines equivalence relations as relations that are reflexive, symmetric, and transitive. It proves that an equivalence relation partitions a set into disjoint equivalence classes, illustrating this with the construction of rational numbers as an example.

3.4.1 Definition of Equivalence Relations

Definition 3.19:

An equivalence relation $R$ on a set $A$ is a binary relation that satisfies three properties for all elements $a$, $b$, and $c$ in $A$:

1. Reflexivity: $aRa$ (Every element is related to itself).

2. Symmetry: If $aRb$, then $bRa$ (If $a$ is related to $b$, then $b$ is related to $a$).

3. Transitivity: If $aRb$ and $bRc$, then $aRc$ (If $a$ is related to $b$, and $b$ is related to $c$, then $a$ is related to $c$).

Examples:

• Example 3.31: The equality relation "$=$" on any set $A$ is an equivalence relation. For all $a\in A$, $a=a$ (reflexive), if $a=b$, then $b=a$ (symmetric), and if $a=b$ and $b=c$, then $a=c$ (transitive).

• Example 3.32: The congruence modulo $m$ relation (${\equiv }_m$) on integers is an equivalence relation. For integers $a$, $b$, and $c$:

  • Reflexivity: $a{\equiv }_{m}a$ because $m|(a-a)=0$.
  • Symmetry: If $a{\equiv }_{m}b$ (meaning $m|(a-b)$), then $m|(b-a)=-(a-b)$, so $b{\equiv }_{m}a$.
  • Transitivity: If $a{\equiv }_{m}b$ ($m|(a-b)$) and $b{\equiv }_{m}c$ ($m|(b-c)$), then $m|((a-b)+(b-c))=(a-c)$, so $a{\equiv }_{m}c$.

• Example 3.33: On the set of points in the plane, define a relation $R$ such that two points are related if they lie on the same line parallel to the line $y=-x$. This is an equivalence relation:

  • Reflexivity: A point always lies on the same line parallel to y = -x that passes through itself.
  • Symmetry: If points $A$ and $B$ lie on the same line parallel to y = -x, then $B$ and $A$ lie on the same line parallel to y = -x.
  • Transitivity: If points $A$ and $B$ lie on the same line parallel to y = -x, and points $B$ and $C$ lie on the same line parallel to y = -x, then points $A$ and $C$ must lie on the same line parallel to y = -x.

The Intersection of Equivalence Relations

Lemma 3.10: The intersection of two equivalence relations on the same set is also an equivalence relation.

Proof:

Let $R_1$ and $R_2$ be two equivalence relations on a set $A$. We need to show that their intersection, denoted by $R_1\cap R_2$, is also an equivalence relation. To do this, we need to prove that $R_1\cap R_2$ satisfies reflexivity, symmetry, and transitivity.

1. Reflexivity: For any $a\in A$, since $R_1$ and $R_2$ are equivalence relations, we have $a{R}_{1}a$ and $a{R}_{2}a$. Therefore, $a(R_1\cap R_2)a$, demonstrating reflexivity for $R_1\cap R_2$.

2. Symmetry: Let $a,b\in A$ such that $a(R_1\cap R_2)b$. By definition of intersection, this means $a{R}_{1}b$ and $a{R}_{2}b$. Since $R_1$ and $R_2$ are symmetric, we also have $b{R}_{1}a$ and $b{R}_{2}a$. Therefore, $b(R_1\cap R_2)a$, demonstrating symmetry for $R_1\cap R_2$.

3. Transitivity: Let $a,b,c\in A$ such that $a(R_1\cap R_2)b$ and $b(R_1\cap R_2)c$. This implies $a{R}_{1}b$, $a{R}_{2}b$, $b{R}_{1}c$, and $b{R}_{2}c$. Because $R_1$ and $R_2$ are transitive, we have $a{R}_{1}c$ and $a{R}_{2}c$. Therefore, $a(R_1\cap R_2)c$, demonstrating transitivity for $R_1\cap R_2$.

Since $R_1\cap R_2$ satisfies reflexivity, symmetry, and transitivity, it is an equivalence relation. Therefore, Lemma 3.10 is proven.

Example 3.34 (Illustrative):

Consider the equivalence relations ${\equiv }_3$ (congruence modulo 3) and ${\equiv }_5$ (congruence modulo 5) on the set of integers $\mathbb{Z}$. Their intersection, ${\equiv }_3\cap {\equiv }_5$, is the equivalence relation ${\equiv }_{15}$ (congruence modulo 15). This demonstrates Lemma 3.10 in a concrete case. Each equivalence class in ${\equiv }_{15}$ is a subset of an equivalence class in both ${\equiv }_3$ and ${\equiv }_5$.

3.4.2 Equivalence Classes Form a Partition

Definition 3.21:

A partition of a set $A$ is a collection of non-empty, pairwise disjoint subsets (called cells or blocks) of $A$ whose union is $A$.

Theorem 3.11:

Given an equivalence relation $R$ on a set $A$, the equivalence classes of $R$ form a partition of $A$.

Proof:

Let $R$ be an equivalence relation on $A$. The equivalence class of an element $a\in A$ is defined as $[a{]}_R=\{x\in A\mid aRx\}$. (We can drop the subscript if the relation is clear.)

1. Every element belongs to at least one equivalence class: By reflexivity ($aRa$), $a$ belongs to its own equivalence class $[a]$. Therefore, ${\bigcup }_{a\in A}[a]=A$.

2. Equivalence classes are disjoint: Suppose $[a]\cap [b]\ne \varnothing$ for some $a,b\in A$. This means there exists an element $c$ such that $c\in [a]$ and $c\in [b]$. By definition, $aRc$ and $bRc$. By symmetry, $cRb$. By transitivity, $aRb$. Now, if $x\in [a]$, then $aRx$. Since $aRb$ and $bRx$, we have $aRx$ by transitivity, thus $x\in [b]$, which means $[a]\subseteq [b]$. A similar argument shows $[b]\subseteq [a]$. Therefore, $[a]=[b]$. Thus, any two equivalence classes are either identical or disjoint.

3. Therefore, the set of equivalence classes $\{[a]\mid a\in A\}$ forms a partition of $A$.

3.4.3 Example: Definition of the Rational Numbers

The set of rational numbers, $\mathbb{Q}$, can be elegantly defined using equivalence classes.

Construction:

1. Universe: Consider the set of ordered pairs of integers $A=\mathbb{Z}\times (\mathbb{Z}\setminus \{0\})$. An element $(a,b)\in A$ intuitively represents the fraction $\frac{a}{b}$.

2. Equivalence Relation: We define the relation $\sim$ on $A$ as follows: $(a,b)\sim (c,d)\iff ad=bc$.

3. Proof that ~ is an equivalence relation:

   • Reflexivity: $(a,b)\sim (a,b)$ because $ab=ba$.
   • Symmetry: If $(a,b)\sim (c,d)$, then $ad=bc$. This implies $cb=da$, so $(c,d)\sim (a,b)$.
   • Transitivity: If $(a,b)\sim (c,d)$ ($ad=bc$) and $(c,d)\sim (e,f)$ ($cf=de$), then $adf=bce$. Since $d\ne 0$, we can divide both sides to obtain $af=be$, implying $(a,b)\sim (e,f)$. The case where $d=0$ is not possible because $(c,d)\in A$ implies $d\ne 0$.

4. Rational Numbers as Equivalence Classes: The rational numbers $\mathbb{Q}$ are defined as the set of equivalence classes of $\sim$: $\mathbb{Q}=A/\sim$. Each equivalence class $[(a,b)]$ represents a rational number, often denoted as $\frac{a}{b}$. Note that many different pairs $(a,b)$ can represent the same rational number (e.g., (1,2), (2,4), (-1,-2) all represent the same rational number).

This construction provides a rigorous and elegant mathematical definition of rational numbers using the concept of equivalence relations and partitions.

3.5 Partial Order Relations

TLDR: This section defines partial order relations, which are reflexive, antisymmetric, and transitive. It introduces Hasse diagrams as a visual representation of partial orders, explores how to combine partial orders (posets) using lexicographical order, and defines special elements within posets (minimal, maximal, least, greatest) and lattice structures (meet, join).

3.5.1 Definition

A partial order is a binary relation, ≤, on a set $A$ that satisfies three properties:

1. Reflexivity: For all $a\in A$, $a\le a$. (Every element is related to itself).

2. Antisymmetry: For all $a,b\in A$, if $a\le b$ and $b\le a$, then $a=b$. (If two elements are related in both directions, they must be the same element).

3. Transitivity: For all $a,b,c\in A$, if $a\le b$ and $b\le c$, then $a\le c$. (If $a$ is related to $b$, and $b$ is related to $c$, then $a$ is related to $c$).

A set $A$ with a partial order ≤ is called a partially ordered set (poset), denoted $(A,\le )$. Note that a partial order doesn’t necessarily relate every pair of elements in $A$. Some elements may be incomparable.

3.5.2 Hasse Diagrams

A Hasse diagram provides a visual representation of a finite poset. It simplifies the representation by omitting:

1. Reflexive edges: Edges from a node to itself (since reflexivity is implied).
2. Transitive edges: If $a\le b$ and $b\le c$, the edge between $a$ and $c$ is implied and omitted.

The diagram uses the vertical positioning of nodes to indicate the ordering: Higher nodes represent larger elements in the partial order.

Example 3.42:

The Hasse diagram for the poset $(\{2,3,4,5,6,7,8,9\},|)$ (where ”|” denotes the “divides” relation) is shown in the textbook figure. This shows that $2|4,2|6,2|8,3|6,3|9$, etc., with no explicit transitive relationships (e.g., $2|6$ and $6|12$, but only $2|12$ is explicitly shown).

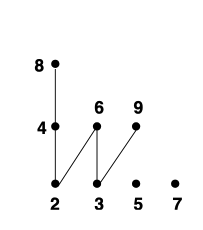
Example 3.43:

The Hasse diagram for $(\{1,2,3,4,6,8,12,24\},|)$ is shown in the textbook figure. This illustrates a more complex poset with multiple levels of divisibility.

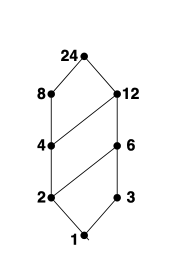
Example 3.44:

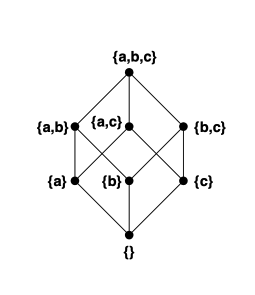
The Hasse diagram for $(P(\{a,b,c\}),\subseteq )$ (where $P(\{a,b,c\})$ represents the power set of $\{a,b,c\}$, and $\subseteq$ denotes the subset relation) illustrates another type of poset, where subsets are ordered by the subset relationship.

Example 3.45:

This example is an exercise ; you are given two Hasse diagrams and asked to identify integer sets with the divisibility relationship that would produce these diagrams. This requires constructing sets of integers where the divisibility relation creates the same structure as in the diagrams.

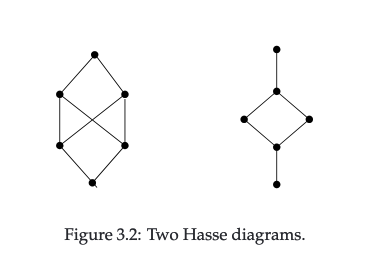
The first diagram could be something like $(\{1,2,3,12,18,144\};|)$ and the second could be something like $(\{2,4,12,20,240,480\};|)$

3.5.3 Combinations of Posets and the Lexicographic Order

We can create new posets by combining existing ones. One method is the lexicographical order:

Definition 3.28: Lexicographical Order

Given two posets $(A,{\le }_A)$ and $(B,{\le }_B)$, their lexicographical product is the poset $(A\times B,{\le }_{lex})$, where:

$(a_1,b_1){\le }_{lex}(a_2,b_2)⟺(a_1{<}_A{a}_2)\vee ((a_1=a_2)\wedge (b_1{\le }_B{b}_2))$

This definition says that $(a_1,b_1)$ is less than or equal to $(a_2,b_2)$ if either $a_1$ is strictly less than $a_2$ according to ${\le }_A$, or if $a_1$ and $a_2$ are equal, and $b_1$ is less than or equal to $b_2$ according to ${\le }_B$. This is analogous to how words are ordered lexicographically in a dictionary.

Theorem 3.12: The Lexicographical Product of Two Posets is a Poset

Statement: Given two posets $(A,{\le }_A)$ and $(B,{\le }_B)$, their lexicographical product $(A\times B,{\le }_{lex})$ is also a poset, where the lexicographical order ${\le }_{lex}$ is defined as:

$(a_1,b_1){\le }_{lex}(a_2,b_2)⟺(a_1{<}_A{a}_2)\vee ((a_1=a_2)\wedge (b_1{\le }_B{b}_2))$

Proof: We need to show that ${\le }_{lex}$ is reflexive, antisymmetric, and transitive.

1. Reflexivity: For any $(a,b)\in A\times B$, we have $(a,b){\le }_{lex}(a,b)$ because $a=a$ and $b{\le }_{B}b$ (since ${\le }_B$ is reflexive).

2. Antisymmetry: Let $(a_1,b_1),(a_2,b_2)\in A\times B$. Suppose $(a_1,b_1){\le }_{lex}(a_2,b_2)$ and $(a_2,b_2){\le }_{lex}(a_1,b_1)$. We need to show that $(a_1,b_1)=(a_2,b_2)$.

   • From $(a_1,b_1){\le }_{lex}(a_2,b_2)$, we have either $a_1{<}_A{a}_2$ or ($a_1=a_2$ and $b_1{\le }_B{b}_2$).

   • From $(a_2,b_2){\le }_{lex}(a_1,b_1)$, we have either $a_2{<}_A{a}_1$ or ($a_2=a_1$ and $b_2{\le }_B{b}_1$).

   • If $a_1{<}_A{a}_2$, then $a_2$ cannot be less than or equal to $a_1$ (by antisymmetry of ${\le }_A$). Thus, we must have $a_1=a_2$ and $b_1{\le }_B{b}_2$ and $b_2{\le }_B{b}_1$. Then, by the antisymmetry of ${\le }_B$, $b_1=b_2$. Therefore $(a_1,b_1)=(a_2,b_2)$.

3. Transitivity: Let $(a_1,b_1),(a_2,b_2),(a_3,b_3)\in A\times B$. Suppose $(a_1,b_1){\le }_{lex}(a_2,b_2)$ and $(a_2,b_2){\le }_{lex}(a_3,b_3)$. We need to show that $(a_1,b_1){\le }_{lex}(a_3,b_3)$.

   • Case 1: $a_1{<}_A{a}_2$. Since ${\le }_A$ is transitive, if $a_1{<}_A{a}_2$ and $a_2{\le }_A{a}_3$, then $a_1{\le }_A{a}_3$. If $a_1{<}_A{a}_3$, then $(a_1,b_1){<}_{lex}(a_3,b_3)$ by the definition of ${\le }_{lex}$. If $a_1=a_3$, then $a_2=a_3$, and the only possibility is that $a_1=a_2=a_3$ and then $b_1{\le }_B{b}_2$ and $b_2{\le }_B{b}_3$, which implies $b_1{\le }_B{b}_3$ because ${\le }_B$ is transitive. Then $(a_1,b_1){\le }_{lex}(a_3,b_3)$.

   • Case 2: $a_1=a_2$ and $b_1{\le }_B{b}_2$. If $a_2{<}_A{a}_3$, then $(a_1,b_1){<}_{lex}(a_3,b_3)$ by the definition of ${\le }_{lex}$. If $a_2=a_3$ (hence $a_1=a_3$), then $b_1{\le }_B{b}_2$ and $b_2{\le }_B{b}_3$, which means $b_1{\le }_B{b}_3$. Therefore $(a_1,b_1){\le }_{lex}(a_3,b_3)$.

Since ${\le }_{lex}$ satisfies reflexivity, antisymmetry, and transitivity, $(A\times B,{\le }_{lex})$ is a poset.

Theorem 3.13: A Different Combination Yielding a Partial Order

Statement: For given posets $(A,{\le }_A)$ and $(B,{\le }_B)$, the relation ${\le }_{lex}$ defined on $A\times B$ by:

$(a_1,b_1){\le }_{lex}(a_2,b_2)⟺(a_1{<}_A{a}_2)\vee ((a_1=a_2)\wedge (b_1{\le }_B{b}_2))$

is a partial order relation.

Proof: This proof is very similar to the previous one and again involves showing reflexivity, antisymmetry, and transitivity.

1. Reflexivity: This follows directly from the reflexivity of ${\le }_A$ and ${\le }_B$ because $(a,b){\le }_{lex}(a,b)$ for all $(a,b)\in A\times B$ since $a=a$ and $b{\le }_{B}b$.

2. Antisymmetry: If $(a_1,b_1){\le }_{lex}(a_2,b_2)$ and $(a_2,b_2){\le }_{lex}(a_1,b_1)$, then the only way this can be true is if $a_1=a_2$ and $b_1{\le }_B{b}_2$ and $b_2{\le }_B{b}_1$. By antisymmetry of ${\le }_B$, $b_1=b_2$. Therefore $(a_1,b_1)=(a_2,b_2)$.

3. Transitivity: Suppose $(a_1,b_1){\le }_{lex}(a_2,b_2)$ and $(a_2,b_2){\le }_{lex}(a_3,b_3)$. We need to show $(a_1,b_1){\le }_{lex}(a_3,b_3)$.

   • If $a_1{<}_A{a}_2$, then since $a_2{\le }_A{a}_3$, by transitivity of ${\le }_A$, we have $a_1{<}_A{a}_3$, so $(a_1,b_1){<}_{lex}(a_3,b_3)$.

   • If $a_1=a_2$ and $b_1{\le }_B{b}_2$, then if $a_2{<}_A{a}_3$, we again have $a_1{<}_A{a}_3$ and $(a_1,b_1){<}_{lex}(a_3,b_3)$. If $a_2=a_3$, then $a_1=a_2=a_3$ and $b_1{\le }_B{b}_2$ and $b_2{\le }_B{b}_3$, which implies $b_1{\le }_B{b}_3$ (transitivity of ${\le }_B$), and therefore $(a_1,b_1){\le }_{lex}(a_3,b_3)$.

Therefore, ${\le }_{lex}$ is a partial order.

3.5.4 Special Elements in Posets

Consider a poset $(P,\le )$. Certain elements have special properties based on the relationship ≤:

Definitions:

• Minimal Element: An element $a\in P$ is minimal if there’s no $b\in P$ such that $b<a$ ($b\le a$ and $b\ne a$). There can be multiple minimal elements.

• Maximal Element: An element $a\in P$ is maximal if there’s no $b\in P$ such that $a<b$. There can be multiple maximal elements.

• Least Element: An element $a\in P$ is the least element if $a\le b$ for all $b\in P$. There can only be at most one least element.

• Greatest Element: An element $a\in P$ is the greatest element if $b\le a$ for all $b\in P$. There can only be at most one greatest element.

Example 3.47:

This example, using the Hasse diagram from Example 3.42, illustrates minimal, maximal, least, and greatest elements within that poset (Note: the example specifies that 2, 3, 5, and 7 are minimal elements, and 5, 6, 7, 8, and 9 are maximal elements in Figure 3.1. There is no least element nor greatest element).

Example 3.48:

This example, using the Hasse diagram from Example 3.43, demonstrates a poset with both a least and a greatest element. This involves finding the greatest lower bound and least upper bound of particular subsets.

Example 3.49:

This example examines the poset $(P(\{a,b,c\}),\subseteq )$, which is shown in the Hasse diagram from Example 3.44. It is shown to have both a least and a greatest element.

Example 3.50:

The example highlights that a poset may have a least element but not a greatest element (or vice-versa). This is shown by analyzing $({\mathbb{Z}}^{+},|)$, where ${\mathbb{Z}}^{+}$ are the positive integers and $|$ is the “divides” relation. $1$ is the least element.

3.5.5 Meet, Join, and Lattices

These concepts describe special relationships between elements in a poset:

Definitions:

• Meet ($\wedge$): The meet of two elements $a$ and $b$ in a poset is their greatest lower bound. That is, the largest element $c$ such that $c\le a$ and $c\le b$.

• Join ($\vee$): The join of two elements $a$ and $b$ in a poset is their least upper bound. That is, the smallest element $c$ such that $a\le c$ and $b\le c$.

• Lattice: A poset is a lattice if every pair of elements has both a meet and a join.

Example 3.51:

This example shows that $(\mathbb{N},\le )$, $(\mathbb{N}\setminus \{0\},|)$, and $(P(S),\subseteq )$ (where $S$ is any set) are lattices.

Example 3.52:

The example $(\{1,2,3,4,6,8,12,24\},|)$ (from above) is a lattice where the meet is the greatest common divisor and the join is the least common multiple. The example also shows that $(\{2,3,4,5,6,7,8,9\},|)$ is not a lattice (because some pairs lack either a meet or join).

3.6 Functions

TLDR: This section defines functions as a specific type of relation where each element in the domain maps to exactly one element in the codomain. It distinguishes between total and partial functions, injective, surjective, and bijective functions, and introduces function composition and the concept of the image and preimage of a set under a function.

Definition of a Function

A function, $f$, from a set $A$ (the domain) to a set $B$ (the codomain), denoted $f:A\to B$, is a relation $f\subseteq A\times B$ satisfying two properties:

1. Totality: Every element in the domain is mapped to at least one element in the codomain. $\forall a\in A\exists b\in B((a,b)\in f)$. We often write this as $\forall a\in A\exists b\in B:f(a)=b$.

2. Uniqueness: Every element in the domain is mapped to at most one element in the codomain. $\forall a\in A\forall b,b^{\prime }\in B(((a,b)\in f\wedge (a,b^{\prime })\in f)\Rightarrow b=b^{\prime })$. We often write this as $\forall a\in A\forall b,b^{\prime }\in B:(f(a)=b\wedge f(a)=b^{\prime })\Rightarrow b=b^{\prime }$.

A function maps each input ($a\in A$) to a unique output ($b\in B$). The notation $f(a)=b$ indicates that the function $f$ maps the element $a$ to the element $b$.

Total Function

A total function is a function where every element in the domain is mapped to exactly one element in the codomain. There are no “undefined” values in the domain ; every input has an output.

Example: Let $f:\mathbb{R}\to \mathbb{R}$ be defined by $f(x)=x^2$. This is a total function because every real number has a unique square. The image of this function is ${\mathbb{R}}_{\ge 0}$ (all non-negative real numbers).

Partial Function

A partial function is a relation that satisfies the uniqueness property of functions but not necessarily the totality property. This means that some elements in the domain may not be mapped to any element in the codomain. In other words, there may be some inputs for which the function is undefined.

Example: Let $g:\mathbb{R}\to \mathbb{R}$ be defined by $g(x)=\frac{1}{x}$. This is a partial function because it is undefined at $x=0$. The function is not defined for every $x\in \mathbb{R}$.

Special Types of Functions

Functions can be further categorized:

Injective Function (One-to-One)

A function $f:A\to B$ is injective (or one-to-one) if different elements in the domain map to different elements in the codomain:

$\forall a,a^{\prime }\in A(a\ne a^{\prime }\Rightarrow f(a)\ne f(a^{\prime }))$ (note for injective functions we can restate it as the converse too)

Example:

Let $h:\mathbb{R}\to \mathbb{R}$ be defined by $h(x)=x+1$. This is injective because if $x_1\ne x_2$, then $x_1+1\ne x_2+1$.

Surjective Function (Onto)

A function $f:A\to B$ is surjective (or onto) if every element in the codomain is the image of at least one element in the domain:

$\forall b\in B\exists a\in A(f(a)=b)$

Example:

Let $i:\mathbb{R}\to {\mathbb{R}}_{\ge 0}$ be defined by $i(x)=x^2$. This is surjective because every non-negative real number is the square of some real number.

Bijective Function

A function $f:A\to B$ is bijective if it is both injective and surjective. This means there’s a one-to-one correspondence between the elements of the domain and codomain.

Example:

Let $j:\mathbb{R}\to \mathbb{R}$ be defined by $j(x)=x+1$. This is a bijective function.

Function Composition

Given functions $f:A\to B$ and $g:B\to C$, their composition, denoted $g\circ f$ or simply $gf$, is a function $g\circ f:A\to C$ defined by $(g\circ f)(a)=g(f(a))$. Function composition is associative, meaning $(h\circ g)\circ f=h\circ (g\circ f)$. Not that by convention we don’t use the “relation composition” order but the “function composition” order (which is in reverse).

Example 3.55:

Let $f(x)=x^3+3$ and $g(x)=2x^2+x$. Then $(g\circ f)(x)=g(f(x))=2(x^3+3{)}^2+(x^3+3)=2x^6+12x^3+18+x^3+3=2x^6+13x^3+21$.

Image and Preimage

For a function $f:A\to B$ and a subset $S\subseteq A$, the image of $S$ under $f$ is $f(S)=\{f(a)|a\in S\}$. For a subset $T\subseteq B$, the preimage of $T$ under $f$ is $f^{-1}(T)=\{a\in A|f(a)\in T\}$.

Example 3.53:

Consider again $f(x)=x^2$. $f([2,3])=[4,9]$ (the image of the interval $[2,3]$). $f^{-1}([4,9])=[-3,-2]\cup [2,3]$ (the preimage of $[4,9]$).

Additional Considerations

1. Set of Functions: The set of all functions from a set $A$ to a set $B$ is denoted as $B^A$. If $A$ and $B$ are finite, $|B^A|=|B{|}^{|A|}$.

2. Function as Relations: A function is a special kind of relation. We defined a function in terms of relations (ordered pairs). The notation $f(a)=b$ is a shorthand for $(a,b)\in f$.

3. Inverse Function: Only bijective functions have an inverse function, denoted $f^{-1}$. The inverse function $f^{-1}:B\to A$ satisfies $f^{-1}(f(a))=a$ for all $a\in A$ and $f(f^{-1}(b))=b$ for all $b\in B$.

These additional points provide a more comprehensive understanding of functions within the context of set theory and relations.

3.7 Countable and Uncountable Sets

TLDR: This section distinguishes between countable and uncountable sets. Countable sets can be put into a one-to-one correspondence with the natural numbers ; uncountable sets cannot. Cantor’s diagonalization argument proves the uncountability of the set of infinite binary sequences, which leads to the important conclusion that uncomputable functions exist.

3.7.1 Countability of Sets

Definition:

A set $A$ is countable if there exists a bijection (a one-to-one and onto mapping) $f:\mathbb{N}\to A$, where $\mathbb{N}=\{1,2,3,...\}$ is the set of natural numbers. This means we can list the elements of $A$ as $a_1,a_2,a_3,...$ A finite set is also considered countable.

Examples:

• Example 3.56: The set of integers $\mathbb{Z}=\{...,-2,-1,0,1,2,...\}$ is countable. A bijection $f:\mathbb{N}\to \mathbb{Z}$ can be defined as: $f(n)=\{\begin{array}{ll}\frac{n}{2}& \text{if }n\text{ is even}\\ -\frac{n-1}{2}& \text{if }n\text{ is odd}\end{array}$

• Example 3.57: The set of odd natural numbers $O=\{1,3,5,...\}$ is countable. A bijection $f:\mathbb{N}\to O$ is $f(n)=2n-1$.

Lemma 3.15

3.7.2 Between Finite and Countably Infinite

Countably Infinite Sets:

A set is countably infinite if it’s countable but not finite. This means there exists a bijection between the set and the natural numbers, but the listing is infinite.

Example:

The set of natural numbers $\mathbb{N}$ itself is countably infinite.

Theorem 3.17:

A set A is countable if and only if it is finite or $A\sim \mathbb{N}$. (There’s no cardinality between finite and countably infinite.)

Proof:

• ($⟹$) If A is finite, it’s countable by definition. If A is countably infinite, by definition there’s a bijection between A and $\mathbb{N}$, so $A\sim \mathbb{N}$.

• ($⟸$) If A is finite, it’s countable. If $A\sim \mathbb{N}$, then A is countably infinite (and hence countable).

3.7.3 Important Countable Sets

• Example 3.56: The set of natural numbers $\mathbb{N}=\{1,2,3,...\}$ is countable.

• Example 3.56: The set of integers $\mathbb{Z}=\{...,-2,-1,0,1,2,...\}$ is countable.

• Example 3.21: The set of rational numbers $\mathbb{Q}$ is countable.

  This is less obvious and requires a proof. The standard proof involves creating a list of rational numbers by organizing the fractions $p/q$ (where $p\in \mathbb{Z}$ and $q\in \mathbb{N}$) in a specific pattern (such as diagonals). See: Simple Proof

3.7.4 Uncountability of $\{0,1{\}}^{\infty }$

Definition:

$\{0,1{\}}^{\infty }$ denotes the set of all infinite sequences consisting of 0s and 1s. Each sequence represents a function $f:\mathbb{N}\to \{0,1\}$.

Theorem 3.23:

The set $\{0,1{\}}^{\infty }$ is uncountable.

Proof (by contradiction):

1. Assumption: Assume $\{0,1{\}}^{\infty }$ is countable. Then there exists a bijection $f:\mathbb{N}\to \{0,1{\}}^{\infty }$. This allows us to list all the infinite sequences:

   $f(1)=(a_{11},a_{12},a_{13},...)$ $f(2)=(a_{21},a_{22},a_{23},...)$ $f(3)=(a_{31},a_{32},a_{33},...)$ …

2. Diagonalization Argument: Construct a new sequence $(b_1,b_2,b_3,...)$ where:

   $b_i=\{\begin{array}{ll}1& \text{if }{a}_{ii}=0\\ 0& \text{if }{a}_{ii}=1\end{array}$

3. Contradiction: This sequence $(b_1,b_2,b_3,...)$ differs from every sequence in the original list $f(i)$ in at least one position (the $i$-th position). But, if $f$ is a bijection, then $(b_1,b_2,b_3,...)$ must be equal to $f(k)$ for some $k\in \mathbb{N}$. This creates a contradiction.

4. Conclusion: Our initial assumption that $\{0,1{\}}^{\infty }$ is countable must be false. Therefore, $\{0,1{\}}^{\infty }$ is uncountable.

3.7.5 Existence of Uncomputable Functions

Theorem 3.24 (Corollary):

There exist uncomputable functions $f:\mathbb{N}\to \{0,1\}$.

Proof:

1. Every computer program can be represented as a finite binary string (and thus as a natural number).

2. The set of all such programs is therefore countable.

3. The set of all functions $f:\mathbb{N}\to \{0,1\}$ is equinumerous with $\{0,1{\}}^{\infty }$ and hence uncountable.

4. Since the number of functions $f:\mathbb{N}\to \{0,1\}$ is larger than the number of programs, it follows that there must exist functions that cannot be computed by any program.