06 Set Theory and Russels Paradox

Set Theory

Set theory is the mathematical study of collections, called sets, and their relationships.

Basic Definitions

• Set: A well-defined collection of distinct objects called elements. Formally, a set $S$ is denoted by curly braces: $\{e_1,e_2,...,e_n\}$ where each $e_i$ is an element of $S$.
• Element: An individual object contained within a set. The symbol $\in$ indicates membership in a set. For example, if $A=\{1,2,3\}$, then $2\in A$ but $4\notin A$.
• Empty Set: A set containing no elements, denoted by $\varnothing$ or {}.

Set Operations

• Union ($\cup$): The union of two sets $A$ and $B$, denoted $A\cup B$, is the set containing all elements that are in either $A$, $B$, or both.
• Intersection ($\cap$): The intersection of two sets $A$ and $B$, denoted $A\cap B$, is the set containing all elements common to both $A$ and $B$.
• Difference (- or \): The difference of two sets $A$ and $B$, denoted $AB$, is the set containing all elements that are in $A$ but not in $B$.
• Subset ($\subseteq$): Set $A$ is a subset of set $B$ (denoted $A\subseteq B$) if every element of $A$ is also an element of $B$.

Union & Intersection:

Difference:

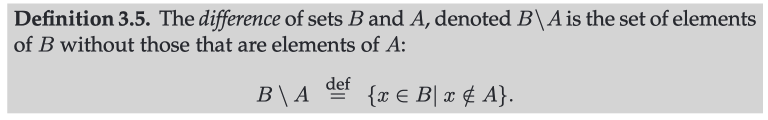
Subset:

Russell’s Paradox

Imagine a special set called “R” that contains all sets that don’t contain themselves as members. Sounds straightforward, right?

Now, here’s the mind-bending part: Does “R” contain itself?

• If “R” does contain itself, then it breaks its own rule – it shouldn’t include sets that contain themselves!
• If “R” doesn’t contain itself, well, that means it should be in the set because it fits the description of a set that doesn’t contain itself.

This paradox can be represented mathematically:

Let $R=\{A|A\notin A\}$

where the notation $\{A|...\}$ denotes the set comprehension, meaning “the set of all $A$ such that…“.

• Contradiction: We have a contradiction! If $R\in R$, then by definition $R\notin R$. Conversely, if $R\notin R$, then it should belong to $R$ according to its own definition.

This paradox demonstrates the danger of defining sets without strict rules. Mathematicians needed a more rigorous foundation for set theory to avoid such contradictions.

The Foundation: The Universe Set and Constructing Natural Numbers

Zermelo’s axiomatic set theory addressed these issues by introducing a Universe Set, denoted $U$, which contains all possible sets. This provides a clear starting point and avoids the ambiguity of an undefined “all sets.” Crucially, we begin with the Empty Set, $\varnothing$, as it requires no elements and acts as a fundamental building block for constructing other sets.

Within this framework, new sets are constructed using specific axioms. Two crucial concepts emerge:

• The Empty Set: This set, denoted $\varnothing$, contains no elements. It serves as the fundamental building block for constructing other sets within the Universe Set.

• Natural Numbers: Using the empty set and the axiom of pairing (which allows us to create a set containing two given elements), we can define natural numbers recursively:

• 0 = $\varnothing$

• 1 = $\{\varnothing \}$

• 2 = $\{\{\varnothing \},\varnothing \}$

• 3 = $\{\{\varnothing \},\{\{\varnothing \}\},\{\varnothing \},\varnothing \}$

• … and so on.

Each natural number is defined as a specific set, built from the empty set using pairing. This avoids the pitfalls of Russell’s Paradox because each set has a clear definition within the framework of the Universe Set and its axioms.

Zermelo’s approach provides a solid foundation for set theory, avoiding the pitfalls of Russell’s Paradox and enabling the construction of complex mathematical structures with precise definitions.

If we were delving deeper into traditional mathematics, we’d naturally progress to defining operations like addition and multiplication for these sets representing natural numbers. However, in computer science, our focus is more practical. We’re less concerned with the abstract theoretical underpinnings and more interested in how these concepts can be used to build and understand real-world systems.

Continue here: 07 Equality, Ordered Pairs, Cartesian Product, Power Set and Relationships