02 Vectors

Lecture from 20.09.2024 | Video: Videos ETHZ

Vectors Collections and Representations

Sequence of vectors

A sequence of vectors can be represented as a tuple. These elements are ordered and may occur more than once.

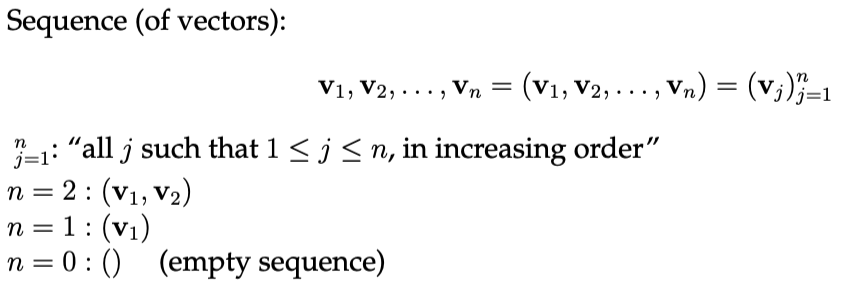
Note that when you have an element of no vectors, you get the empty sequence (since you unable to fill the sequence with any vectors).

Set of vectors

Similarly, you can also define a set of vectors. These are unordered “sets” with unique elements (if you have the same vector twice, it’s only “found once” in the set). One can imagine them as being a “bag” out of which we can pick unique vectors.

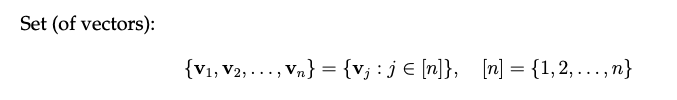
Sum of vectors

To sum up vectors (i.e. add them up from the origin) we can use the following notation.

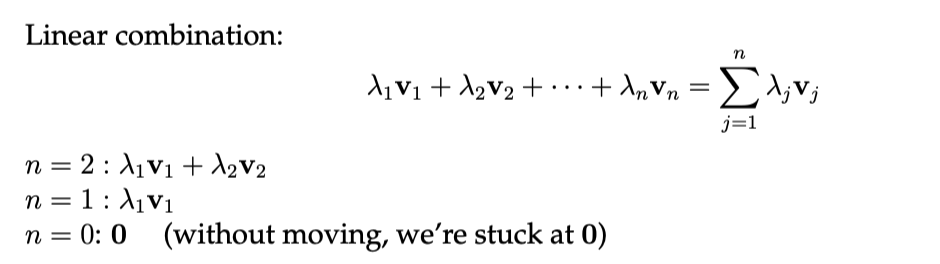
Note that when you are summing up no vectors, your position doesn’t change (from the origin where you started at). The origin is defined by the null vector $0$ “bold zero” and is the zero vector in ${\mathbb{R}}^n$. Meaning, in 2d you’d have $\left[\begin{array}{c}0\\ 0\end{array}\right]$. In 3d you’d have $\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$ and so forth.

Column Vector Builder Notation

Another way of defining vectors is to define how each i-th element of a vector produced as a function of i.

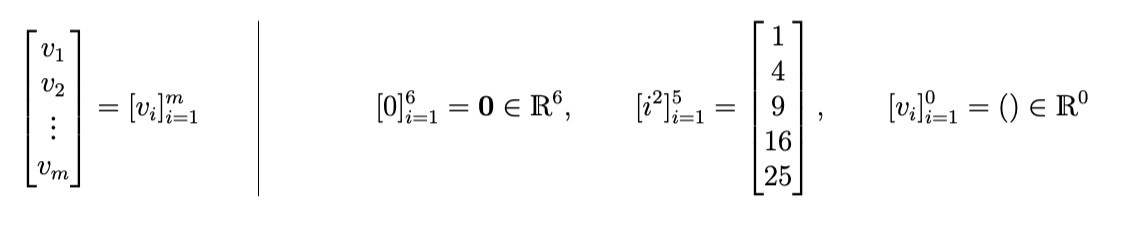
In the example in the middle it is important to mention that the “bold zero” is not the number zero but the zero vector (=Nullvector). The zero vector for any ${\mathbb{R}}^n$ is a vector of size $n$ filled with zeros. For ${\mathbb{R}}^0$ you’ll have an empty vector (since $i=1$ going to $m$ gives you an empty set → no $v_m$ element to put into the vector).

Length of a vector

The length (or magnitude) of a vector is a measure of how long the vector is. In mathematics, this is often referred to as the Euclidean norm.

For a vector $\mathbf{v}=(v_1,v_2,\dots ,v_n)$, the Euclidean norm is calculated as:

$$|\mathbf{v}|=\sqrt{v_1^2+v_2^2+\dots +v_n^2}=\sqrt{\sum _{i=1}^n{v}_i^2}$$

Why Does Squaring and Taking the Square Root Give the Length?

The reason why squaring each component, summing them up, and then taking the square root gives the length of the vector is rooted in Pythagoras’ theorem. This theorem forms the foundation for understanding distances in both 2D, 3D, and higher dimensions.

2D Case

In 2D, consider a vector $\mathbf{v}=(v_1,v_2)$. You can think of this vector as forming the diagonal of a right triangle, where $v_1$ is the length along the $x$-axis and $v_2$ is the length along the $y$-axis. Using Pythagoras’ theorem, we calculate the length of the diagonal (hypotenuse) as:

$$|\mathbf{v}|=\sqrt{v_1^2+v_2^2}$$

This gives the vector’s length in 2D, corresponding to the straight-line distance between the origin and the point $(v_1,v_2)$.

3D Case

Now consider a vector $\mathbf{v}=(v_1,v_2,v_3)$ in 3D space. Here’s how the same reasoning extends:

1. First, imagine the projection of the vector onto the $xy$-plane. The length of this projection (ignoring the $z$-axis) is given by the 2D formula:

   $$\text{Length in the }xy\text{-plane}=\sqrt{v_1^2+v_2^2}$$

2. Now, treat this projection as one side of a right triangle, and the $z$-component, $v_3$, as the other side. Applying Pythagoras’ theorem in 3D:

   $$|\mathbf{v}|=\sqrt{(\sqrt{v_1^2+v_2^2}{)}^2+v_3^2}=\sqrt{v_1^2+v_2^2+v_3^2}$$

Higher Dimensions (4D and Beyond)

This logic naturally extends to higher dimensions. In 4D, the length of a vector $\mathbf{v}=(v_1,v_2,v_3,v_4)$ is found by treating the 3D vector $(v_1,v_2,v_3)$ as one side of a new triangle, with $v_4$ being the new perpendicular component:

$$|\mathbf{v}|=\sqrt{(\sqrt{v_1^2+v_2^2+v_3^2}{)}^2+v_4^2}=\sqrt{v_1^2+v_2^2+v_3^2+v_4^2}$$

This process continues in higher dimensions. The formula $\sqrt{v_1^2+v_2^2+\dots +v_n^2}$ works for any number of dimensions because each new component is added perpendicularly, just like in Pythagoras’ theorem. Each dimension adds a new “side” to the generalized right triangle.

Unit Vectors

A unit vector is a vector that has a length of 1. It points in the same direction as the original vector but has been scaled down to have a magnitude of 1. Unit vectors are important because they allow us to represent direction without worrying about the magnitude.

To convert a vector $\mathbf{v}$ into a unit vector $\hat{\mathbf{v}}$, we divide the vector by its length:

$$\hat{\mathbf{v}}=\frac{\mathbf{v}}{|\mathbf{v}|}$$

Why care about Unit Vectors

A unit vector is essentially a “pure” direction vector. While a regular vector contains both direction and magnitude (for example, velocity), the unit vector keeps only the direction. Unit vectors are useful in defining directions like $\hat{\mathbf{i}}$ (unit vector along the $x$-axis) or $\hat{\mathbf{j}}$ (unit vector along the $y$-axis).

In higher dimensions, unit vectors help standardize direction regardless of how many components a vector has. For example, in physics, unit vectors are often used to express forces or velocities as directions independent of magnitude.

Dot Product (Scalar Product)

The dot product, also known as the scalar product or inner product, is an operation that takes two vectors and returns a single scalar (a number). It measures how much two vectors “point” in the same direction.

Given two vectors $\mathbf{a}=(a_1,a_2,\dots ,a_n)$ and $\mathbf{b}=(b_1,b_2,\dots ,b_n)$, their dot product is defined as:

$$\mathbf{a}\cdot \mathbf{b}=a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n=\sum _{i=1}^n{a}_i{b}_i$$

Dot product can be written using the angle $\theta$ between the two vectors:

$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos (\theta )$$

where $|\mathbf{a}|$ and $|\mathbf{b}|$ are the magnitudes (lengths) of the vectors, and $\theta$ is the angle between them. A simpler way to understand this is to understand that the $\cos (\theta )$ is equal to the dot product of the normalised vectors.

$$\cos (\theta )=\left(\frac{\mathbf{a}}{|a|}\right)\cdot \left(\frac{\mathbf{b}}{|b|}\right)$$

Intuition

The dot product gives a sense of how aligned two vectors are:

• When the vectors point in the same direction: The dot product is positive and large. The cosine of a small angle (close to 0) is close to 1, meaning the vectors are nearly parallel.
• When the vectors are perpendicular: The dot product is 0. This happens because $\cos (90^{\circ })=0$, so the vectors have no overlap in their directions.
• When the vectors point in opposite directions: The dot product is negative. The cosine of an angle near $180^{\circ }$ is close to $-1$, meaning the vectors are pointing in opposite directions.

Geometric Intuition

Think of the dot product as a measure of how much one vector contributes to another in terms of direction. Imagine projecting one vector onto the direction of another:

• If the two vectors align perfectly, the projection will be large, giving a large positive result.
• If they are perpendicular, the projection is zero (because there’s no overlap in direction).
• If the vectors are opposite, the projection will be negative, indicating the vectors are pulling in opposite directions.

The dot product is fundamental in determining angles between vectors and checking orthogonality (perpendicularity) in geometry and physics.

Note: If you want to dive deeper into actually why a dot product is related to a projection I suggest you watch this video by 3b1b.

Inequalities to know

Cauchy-Schwarz Inequality

The Cauchy-Schwarz Inequality states that for any two vectors $\mathbf{a}$ and $\mathbf{b}$, the absolute value of their dot product is less than or equal to the product of their magnitudes:

$$|\mathbf{a}\cdot \mathbf{b}|\le |\mathbf{a}|\ast |\mathbf{b}|$$

Equality holds if and only if the vectors $\mathbf{a}$ and $\mathbf{b}$ are linearly dependent (i.e., they point in the same or exactly opposite directions).

Proof of the Cauchy-Schwarz Inequality

Triangle Inequality

The Triangle Inequality is a fundamental property of norms (or lengths) in vector spaces. It states that for any two vectors $\mathbf{u}$ and $\mathbf{v}$, the length of their sum is less than or equal to the sum of their lengths:

$$|\mathbf{u}+\mathbf{v}|\le |\mathbf{u}|+|\mathbf{v}|$$

Intuitive Understanding

To understand this inequality intuitively, consider the following:

• Imagine two vectors $\mathbf{u}$ and $\mathbf{v}$ represented as arrows in a plane. The triangle inequality tells us that if you take one arrow (vector) and place the tail of the second arrow at the head of the first arrow, the direct path from the tail of the first arrow to the head of the second arrow (which is the vector sum $\mathbf{u}+\mathbf{v}$) is always shorter than or equal to the sum of the lengths of the two arrows (the lengths of $\mathbf{u}$ and $\mathbf{v}$).

• This is similar to navigating in a straight line versus taking two segments of a path. The direct route (the length of the vector sum) cannot exceed the total distance traveled along the two segments (the lengths of the individual vectors).

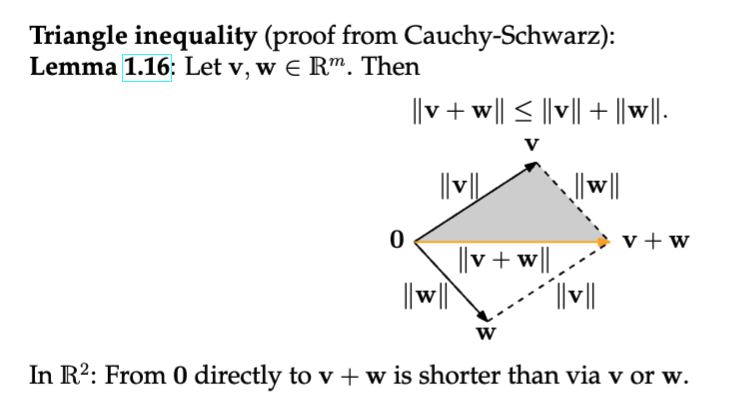
Proof of the Triangle Inequality

Now, let’s prove the triangle inequality using the properties of the magnitude:

1. Start with the expression for the square of the length of the sum:

   $$\Vert \mathbf{u}+\mathbf{v}{\Vert }^2=(\mathbf{u}+\mathbf{v})\cdot (\mathbf{u}+\mathbf{v})=\Vert \mathbf{u}{\Vert }^2+\Vert \mathbf{v}{\Vert }^2+2(\mathbf{u}\cdot \mathbf{v})$$

2. Apply the Cauchy-Schwarz Inequality:

   By the Cauchy-Schwarz inequality, we know:

   $$|\mathbf{u}\cdot \mathbf{v}|\le \Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert$$

   This implies:

   $$2(\mathbf{u}\cdot \mathbf{v})\le 2\Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert$$

3. Combine the results:

   From the expression for $\Vert \mathbf{u}+\mathbf{v}{\Vert }^2$, we can substitute the upper bound for the dot product:

   $$\Vert \mathbf{u}+\mathbf{v}{\Vert }^2\le \Vert \mathbf{u}{\Vert }^2+\Vert \mathbf{v}{\Vert }^2+2\Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert$$

   The right side can be factored as:

   $$\Vert \mathbf{u}+\mathbf{v}{\Vert }^2\le (\Vert \mathbf{u}\Vert +\Vert \mathbf{v}\Vert {)}^2$$

4. Taking the square root:

   Finally, taking the square root of both sides yields:

   $$\Vert \mathbf{u}+\mathbf{v}\Vert \le \Vert \mathbf{u}\Vert +\Vert \mathbf{v}\Vert$$

Thus, the triangle inequality is proven.

Continue here: 03 Linear Dependence and Independence