05 Proof Types

Lecture from: 02.10.2024 | Video: Videos ETHZ

---

In discrete mathematics, rigorous proof is essential for establishing the validity of mathematical statements. Todays lecture will introduce several fundamental proof techniques commonly used in discrete mathematics.

Composition of Implications

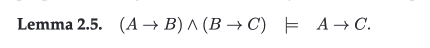
This theorem, demonstrating the principle of transitivity of implication, provides a fundamental tool for constructing proofs in discrete mathematics.

Theorem: If $(S⟹T)$ and $(T⟹U)$, then $S⟹U$.

Proof by Truth Table:

$S$	$T$	$U$	$S\Rightarrow T$	$T\Rightarrow U$	$(S\Rightarrow T)\wedge (T\Rightarrow U)$	$S\Rightarrow U$
T	T	T	T	T	T	T
T	T	F	T	F	F	F
T	F	T	F	T	F	T
T	F	F	F	T	F	F
F	T	T	T	T	T	T
F	T	F	T	F	F	T
F	F	T	T	T	F	T
F	F	F	T	T	F	T

As shown in the truth table, whenever $(S\Rightarrow T)$ and $(T\Rightarrow U)$ are both true, then $S\Rightarrow U$ is also true. Therefore, we have proven that if $(S\Rightarrow T)$ and $(T\Rightarrow U)$, then $S\Rightarrow U$.

As shown in the truth table, whenever $(S\Rightarrow T)$ and $(T\Rightarrow U)$ are both true, then $S\Rightarrow U$ is also true. Therefore, we have proven that if $(S\Rightarrow T)$ and $(T\Rightarrow U)$, then $S\Rightarrow U$.

Theorem: If $(A\Rightarrow B)$ and $(A\Rightarrow C)$, then $A\Rightarrow (B\wedge C)$.

Proof by Truth Table:

A	B	C	$A\Rightarrow B$	$A\Rightarrow C$	$B\wedge C$	$A\Rightarrow (B\wedge C)$
T	T	T	T	T	T	T
T	T	F	T	F	F	F
T	F	T	F	T	F	F
T	F	F	F	F	F	F
F	T	T	T	T	T	T
F	T	F	T	T	F	T
F	F	T	T	F	F	T
F	F	F	T	T	F	T

As shown in the truth table, whenever $(A\Rightarrow B)$ and $(A\Rightarrow C)$ are both true, then $A\Rightarrow (B\wedge C)$ is also true. Therefore, we have proven that if $(A\Rightarrow B)$ and $(A\Rightarrow C)$, then $A\Rightarrow (B\wedge C)$.

Proof of Implications

A fundamental task in discrete mathematics is proving implications. An implication, represented as $P\Rightarrow Q$, states that if $P$ is true, then $Q$ must also be true. It’s important to note that an implication doesn’t necessarily state anything about the truth value of $Q$ when $P$ is false.

Direct Proof of $S⟹T$

Definition: A direct proof starts by assuming the hypothesis ($S$) to be true and then logically deduces the conclusion ($T$).

Example: If a and b are square numbers, then a x b is also a square number.

• $U=\mathbb{N}$
• $S:\exists u\exists v:a=u\cdot u,b=v\cdot v$
• $\dot{⟹}ab=(uu)(vv)$
• $\dot{⟹}ab=u\cdot u\cdot v\cdot v$
• $\dot{⟹}ab=(u\cdot v)(u\cdot v)$
• $\dot{⟹}\exists m:ab=m\cdot m$
• $\dot{⟹}ab\text{ is a square number}$

Contrapositive Proof

A contrapositive proof is a powerful technique in logic. Instead of directly proving an implication $P\Rightarrow Q$, we prove its logically equivalent contrapositive: $\neg Q\Rightarrow \neg P$.

Since these statements always have the same truth value, proving the contrapositive is equivalent to proving the original implication.

Proof of equivalency:

Let us show: $\neg B\to \neg A\equiv A\to B$

$A$	$B$	$\neg B$	$\neg A$	$\neg B\to \neg A$	$A\to B$
T	T	F	F	T	T
T	F	T	F	F	F
F	T	F	T	T	T
F	F	T	T	T	T

As you can see, the columns for $\neg B\to \neg A$ and $A\to B$ have identical truth values in every row. This demonstrates that the original implication and its contrapositive are indeed logically equivalent.

Example: Root of irrational number (>0) is irrational.

• $U={\mathbb{R}}_{>0}$
• $S:x\text{ is irrational}$
• $T:\sqrt{x}\text{ is irrational}$
• $\neg T\dot{⟹}\sqrt{x}\text{ is rational}$
• $\dot{⟹}\sqrt{x}=\frac{m}{n}$
• $\dot{⟹}x=\frac{m^2}{n^2}$
• $\dot{⟹}\exists u\exists v\in \mathbb{Z}:x=\frac{u}{v}$
• $\dot{⟹}x\text{ is rational}$
• $\dot{⟹}\neg S$

Modus Ponens

(Latin for “Mode of Affirming”) is a fundamental rule of inference in logic. It allows us to draw a conclusion from two given premises:

1. Premise 1: If $P$, then $Q$
2. Premise 2: $P$
3. Conclusion: Therefore, $Q$

If we know that “if A happens, then B happens,” and we also know that A does happen, then we can confidently conclude that B must happen.

Proof: $A\wedge (A\to B)\models B$ The truth table is left as an exercise for the reader

Example: $2^{3000}{\equiv }_{3001}1\dot{⟺}{2}^{3000}-1=m\cdot 3001$ for some $m\in \mathbb{Z}$

To solve this, we’ll use a proof (which we haven’t done yet): $\forall n\in \mathbb{N}:(n>2\wedge n\text{ is a prime})⟹2^{n-1}{\equiv }_{n}1$

This means if: $(3001>2\wedge 3001\text{ is a prime})⟹2^{3000}{\equiv }_{3001}1$

This means we only need to prove 3001 is a prime. This would mean we’d have to test all numbers until $\sqrt{3001}$ as divisors.

Proof by Case Distinction

Proof by Case Distinction (or Exhaustive Consideration) is a technique used when we need to prove something about a general case. The strategy involves:

1. Identify Distinct Cases: Break down the overall problem or statement into smaller, mutually exclusive cases.
2. Prove Each Case Individually: Show that the desired conclusion holds true for each individual case separately.
3. Combine Results: Since the cases cover all possibilities, and we’ve proven the conclusion for each case, we can confidently conclude that the statement is true in general.

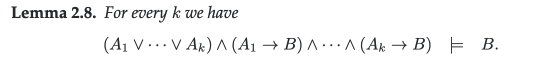
For $k=1$ we would be looking at a Modus Ponens type proof.

Example:

Let’s say we want to prove that for any integer n, the expression $n^2+n$ is even.

1. Case Distinction:

   • Case 1: n is even
   • Case 2: n is odd

2. Prove Each Case:

   • Case 1 (n even): If n is even, we can write it as $n=2k$ where k is an integer. Then $n^2+n=(2k{)}^2+2k=4k^2+2k=2(2k^2+k)$. Since $(2k^2+k)$ is an integer, $n^2+n$ is even.
   • Case 2 (n odd): If n is odd, we can write it as $n=2j+1$ where j is an integer. Then $n^2+n=(2j+1{)}^2+(2j+1)=4j^2+4j+1+2j+1=4j^2+6j+2=2(2j^2+3j+1)$. Since $(2j^2+3j+1)$ is an integer, $n^2+n$ is even.

3. Combine Results: Since we’ve shown that $n^2+n$ is even in both cases (even n and odd n), it must be even for all integers n.

Proof by Contradiction

Alternative Step 3: Prove that $S\vee T\equiv \top$.

Proof by contradiction is a proof technique rooted in the principle of non-contradiction. It leverages the inherent logical inconsistency arising when an assumption leads to a demonstrably false conclusion.

Mathematically, we aim to prove a proposition $P$. The strategy involves:

1. Negation: Assuming the negation of $P$, denoted as $\neg P$.
2. Deduction: Deriving a logical consequence $Q$ from the assumption $\neg P$. This deduction is conducted within the framework of established axioms and previously proven theorems.
3. Contradiction: Demonstrating that $Q$ contradicts a known fact or a previously derived result, establishing an inherent inconsistency in our initial assumption.
4. Conclusion: Since the negation $\neg P$ leads to a logical contradiction, it must be false. Therefore, by the principle of non-contradiction, the original proposition $P$ is true.

Example: Irrationality of $\sqrt{2}$

To demonstrate the power of this technique, consider the classic proof that $\sqrt{2}$ is irrational.

1. Assumption: Assume, for the sake of contradiction, that $\sqrt{2}$ is rational. This implies we can express it as a fraction in its simplest form: $\sqrt{2}=\frac{a}{b}$, where $a$ and $b$ are integers with no common factors.
2. Deduction: Squaring both sides of the equation yields $2=\frac{a^2}{b^2}$, which simplifies to $a^2=2b^2$. This implies that $a^2$ is an even number, and therefore, ‘a’ itself must be even.
3. Contradiction: Let $a=2k$, where $k$ is an integer. Substituting this into the equation $a^2=2b^2$ yields $4k^2=2b^2$, which simplifies to $2k^2=b^2$. This implies that $b^2$ is also even, and consequently, ‘b’ must be even.

Our assumption that $\sqrt{2}$ can be expressed as a fraction with coprime numerator and denominator leads to the contradiction that both ‘a’ and ‘b’ are even.

4. Conclusion: Therefore, our initial assumption that $\sqrt{2}$ is rational must be false, proving that $\sqrt{2}$ is irrational.

Existence Proofs

Demonstrating “Something Exists”

Existence proofs are a type of proof dedicated to showcasing that something exists – a solution to an equation, a specific object with certain properties, or even a mathematical concept itself. Unlike proofs demonstrating a statement’s truth for all cases (like a universal proof), existence proofs simply establish the “being” without necessarily detailing its complete nature or exploring all its properties.

Constructive vs. Non-constructive:

• Constructive existence proofs: Actively construct the desired object or provide a method for generating it. i.e showing a specific example or way to get an example.
• Non-constructive existence proofs: Prove existence without explicitly constructing the object. These often rely on logical arguments and showing that if an object didn’t exist, we’d arrive at a contradiction.

Strategies:

1. Direct Construction: Explicitly build the desired object step-by-step, demonstrating its existence and verifying it satisfies the required properties.
2. Existence by Contradiction: Assume the opposite – that the object doesn’t exist – and derive a contradiction. This contradiction forces us to accept the initial assumption (that the object exists) as true.
3. Pigeonhole Principle: Useful for proving existence when dealing with finite sets and mappings. If you have more pigeons than pigeonholes, at least one pigeonhole must contain more than one pigeon.

Proof by Counterexample

Proof by counterexample is a straightforward yet powerful technique used to disprove universal statements – those claiming something holds true for all cases.

The Core Principle: If you can find just one instance where a universal statement is false, the entire statement is proven incorrect. This single counterexample effectively “breaks” the claim of universality.

Proof by Induction

Proof by induction is a powerful technique for proving statements that hold true for all countable elements of a universe (example $U=\mathbb{N}$).

The Strategy:

1. Base Case: Show the statement holds for the smallest natural number (usually 1).
2. Inductive Hypothesis: Assume the statement is true for some arbitrary natural number k.
3. Inductive Step: Prove that if the statement is true for k, it must also be true for k+1.

Why It Works: If the base case holds and each step guarantees truth for the next number, then the statement holds for all natural numbers. It’s like building a chain – each link depends on the previous one, creating an unbroken sequence.

Continue here: 06 Set Theory and Russels Paradox