05 Transpose and Multiplication

Column Space and Reordering Columns

Reordering columns does not change the rank of a matrix. The independent columns of a matrix span its column space.

Proof

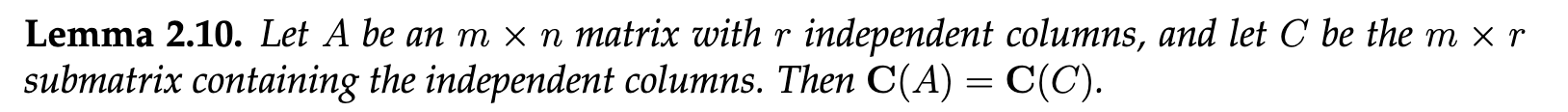
Let $v_1,v_2,\dots ,v_r$ represent the independent columns of a matrix $A$, and let $w_1,w_2,\dots ,w_{n-r}$ represent the dependent columns (ordered as in $A$). The goal is to show that the column space of $A$ remains unchanged even if the columns are reordered.

For each $j$, $w_j$ is a linear combination of $v_1,v_2,\dots ,v_r,w_1,w_2,\dots ,w_{j-1}$, since this sequence includes all the previous independent columns. This implies that:

$$w_j\in \text{span}(v_1,v_2,\dots ,v_r)$$

Now, let’s consider the span of the independent columns: $\text{span}(v_1,v_2,\dots ,v_r)$. By successively adding the dependent columns $w_1,w_2,\dots ,w_{n-r}$, the resulting span remains the same:

$$\text{span}(v_1,v_2,\dots ,v_r,w_1,w_2,\dots ,w_{n-r})=\text{span}(v_1,v_2,\dots ,v_r)$$

This shows that reordering columns does not alter the span of the matrix’s column space, thereby proving the column space remains unchanged.

Transpose of a Matrix

The transpose of a matrix is obtained by flipping the matrix over its diagonal, swapping rows with columns. For example, for a matrix $A$, its transpose is denoted by $A^T$. A useful property is that taking the transpose twice returns the original matrix:

$$(A^T{)}^T=A$$

Symmetric Matrices

A matrix is symmetric if it equals its transpose, i.e., $A=A^T$. This holds for certain special matrices, such as real-valued square matrices with symmetric entries across the diagonal.

Additionally, the column space of a matrix $A$ is the row space of its transpose $A^T$. This shows a dual relationship between row and column spaces.

Matrix Multiplication

Matrix multiplication can be understood as performing multiple linear transformations in sequence. Intuitively, applying matrix $A$ first, followed by matrix $B$, is not the same as applying $B$ first and then $A$. Hence, in general, matrix multiplication is not commutative:

$$AB\ne BA$$

Matrix Multiplication Visualization

Matrix multiplication can be performed row by row, or column by column. For two matrices $A$ (of size $m\times n$) and $B$ (of size $n\times p$), the entry in row $i$ and column $j$ of the product matrix $AB$ is the dot product of the $i$-th row of $A$ with the $j$-th column of $B$.

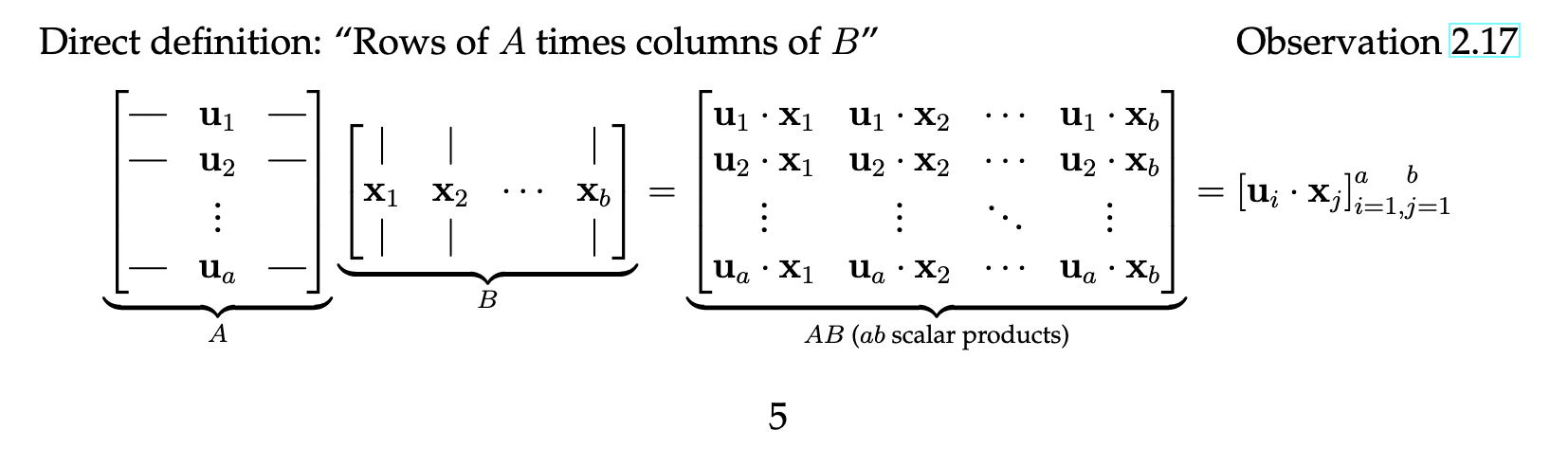
This shows the basic mechanism of matrix multiplication.

Commutativity and the Transpose of a Product

While $AB\ne BA$, an important property of matrix transposition is that the transpose of a product reverses the order of multiplication:

$$(AB{)}^T=B^T{A}^T$$

Inner Product vs. Outer Product

The inner product involves multiplying corresponding elements of two vectors and summing the result. The outer product, on the other hand, multiplies each element of a column vector by each element of a row vector, resulting in a matrix.

Lemma 2.21 (Rank 1 Matrices)

Let $A$ be an $m\times n$ matrix. The following statements are equivalent:

1. $\text{rank}(A)=1$
2. There exist vectors $v\in {\mathbb{R}}^m$ and $w\in {\mathbb{R}}^n$, with $v\ne 0$ and $w\ne 0$, such that:

$$A=v{w}^T$$

This shows that a rank-1 matrix can be expressed as the outer product of two vectors.

Distributive and Associative Properties of Matrix Multiplication

Matrix multiplication follows the distributive property:

$$A(B+C)=AB+AC\text{and}(A+B)C=AC+BC$$

However, matrix multiplication is generally not commutative, meaning that $AB\ne BA$ in most cases. This reflects the fact that applying transformations in a different order results in different outcomes.

The associative property, on the other hand, holds for matrix multiplication:

$$A(BC)=(AB)C$$

This property shows that it doesn’t matter how we group the matrices when multiplying three or more together, as long as the order of multiplication is preserved.

Generally, these properties require separate proofs depending on the dimensions and properties of the matrices involved.