04 Matrices and Linear Combinations

Lecture from 27.09.2024 | Video: Videos ETHZ

Matrix as a Notation for a Sequence of Vectors

A matrix is a way to represent a sequence of vectors, where each vector is either a column or a row in the matrix. 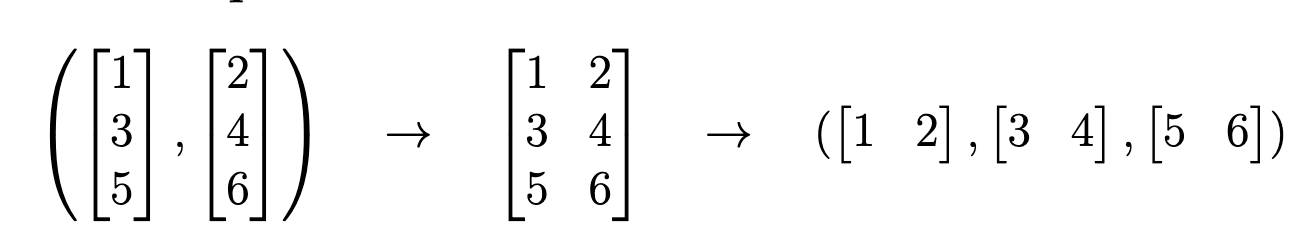Here, $\mathbf{M}$ is a $3\times 2$ matrix, representing a matrix with 3 rows and 2 columns.

Matrix Definition

More generally, an $m\times n$ matrix is a rectangular array of real numbers with $m$ rows and $n$ columns.

For example, an $m\times n$ matrix can be represented as:

$$\mathbf{A}=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]$$

Here, each $a_{ij}$ represents a real number located at the intersection of the $i$th row and $j$th column.

Dot Free Notation

Similar to the “dot-free” notations from vectors (Vector Builder Notation), we can also use a dot-free notation for matrices.

The matrix $A$ can be represented as:

$$A=[a_{ij}{]}_{i=1}^m{,}_{j=1}^n$$

Here, $a_{ij}$ represents the element in the $i$th row and $j$th column, and the matrix has $m$ rows and $n$ columns.

Column and Row Notation

We can represent matrices using column and row notation.

• A column of a matrix consists of all elements vertically aligned in the same column index.
• A row of a matrix consists of all elements horizontally aligned in the same row index.

${\mathbb{R}}^{m\times n}$ Explained

The notation ${\mathbb{R}}^{m\times n}$ represents the set of all matrices with $m$ rows and $n$ columns, where each entry in the matrix is a real number. In other words, it is the space of all $m\times n$ matrices with real entries.

Matrix Addition and Scalar Multiplication

TLDR: Same as vector addition and multiplication

Matrix Addition

Matrix addition is defined for matrices of the same dimensions. If $A$ and $B$ are two $m\times n$ matrices, their sum $A+B$ is a new $m\times n$ matrix where each element is the sum of the corresponding elements in $A$ and $B$.

If:

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]\text{and}B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1n}\\ b_{21}& b_{22}& \cdots & b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ b_{m1}& b_{m2}& \cdots & b_{mn}\end{array}\right]$$

Then the sum $A+B$ is:

$$A+B=\left[\begin{array}{cccc}{a}_{11}+b_{11}& a_{12}+b_{12}& \cdots & a_{1n}+b_{1n}\\ a_{21}+b_{21}& a_{22}+b_{22}& \cdots & a_{2n}+b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}+b_{m1}& a_{m2}+b_{m2}& \cdots & a_{mn}+b_{mn}\end{array}\right]$$

Scalar Multiplication

Scalar multiplication involves multiplying every element of a matrix by a scalar (a real number). If $A$ is an $m\times n$ matrix and $c$ is a scalar, the product $cA$ is obtained by multiplying each element of $A$ by $c$.

If:

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]$$

Then the scalar multiplication $cA$ is:

$$cA=\left[\begin{array}{cccc}c\cdot a_{11}& c\cdot a_{12}& \cdots & c\cdot a_{1n}\\ c\cdot a_{21}& c\cdot a_{22}& \cdots & c\cdot a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ c\cdot a_{m1}& c\cdot a_{m2}& \cdots & c\cdot a_{mn}\end{array}\right]$$

Zero Matrix (Nullmatrix)

A zero matrix (also called a nullmatrix) is a matrix in which all of its entries are zero. It can exist in any size, and is denoted by $0$ or $0_{m\times n}$ for an $m\times n$ matrix.

For example, a $3\times 2$ zero matrix would look like:

$$0_{3\times 2}=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\end{array}\right]$$

The zero matrix has the following properties:

• For any matrix $A$, $A+0=A$ (additive identity).
• For any scalar $c$, $c\cdot 0=0$.

Quadratic Matrix Types

A quadratic matrix is a square matrix where the number of rows equals the number of columns, denoted as ( n \times n ).

Matrix-Vector Multiplication

Matrix-vector multiplication is a fundamental operation in linear algebra, where a matrix is multiplied by a vector to produce a new vector. The multiplication can be interpreted as a linear combination of the columns of the matrix, weighted by the entries of the vector.

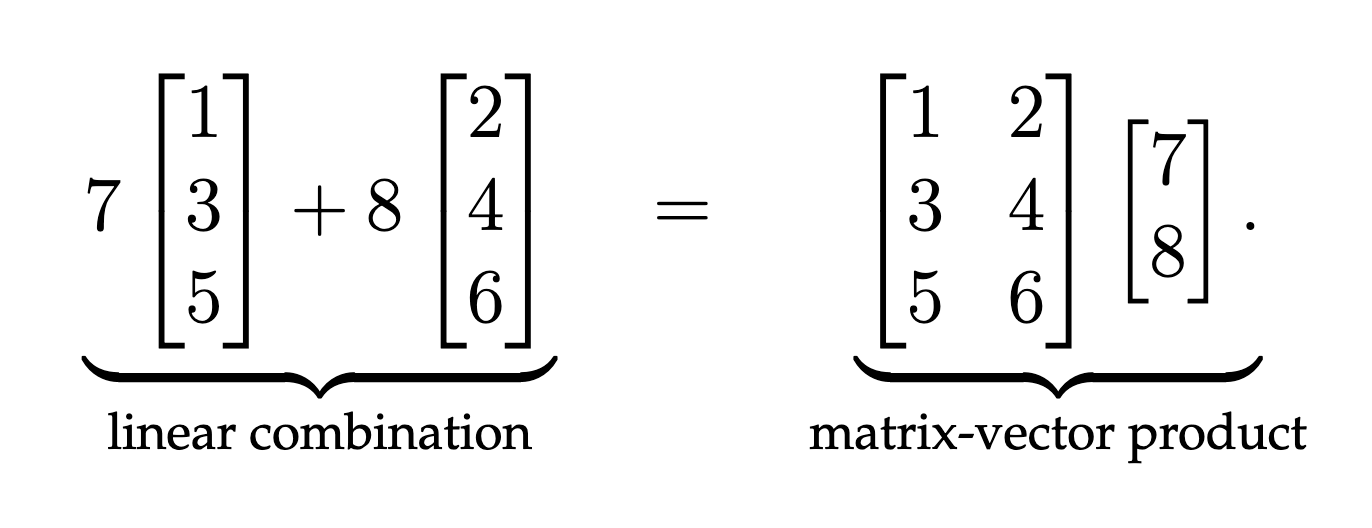
Column Definition

The column definition of matrix-vector multiplication illustrates how the resulting vector can be represented as a linear combination of the matrix’s columns, with the entries of the vector acting as coefficients.

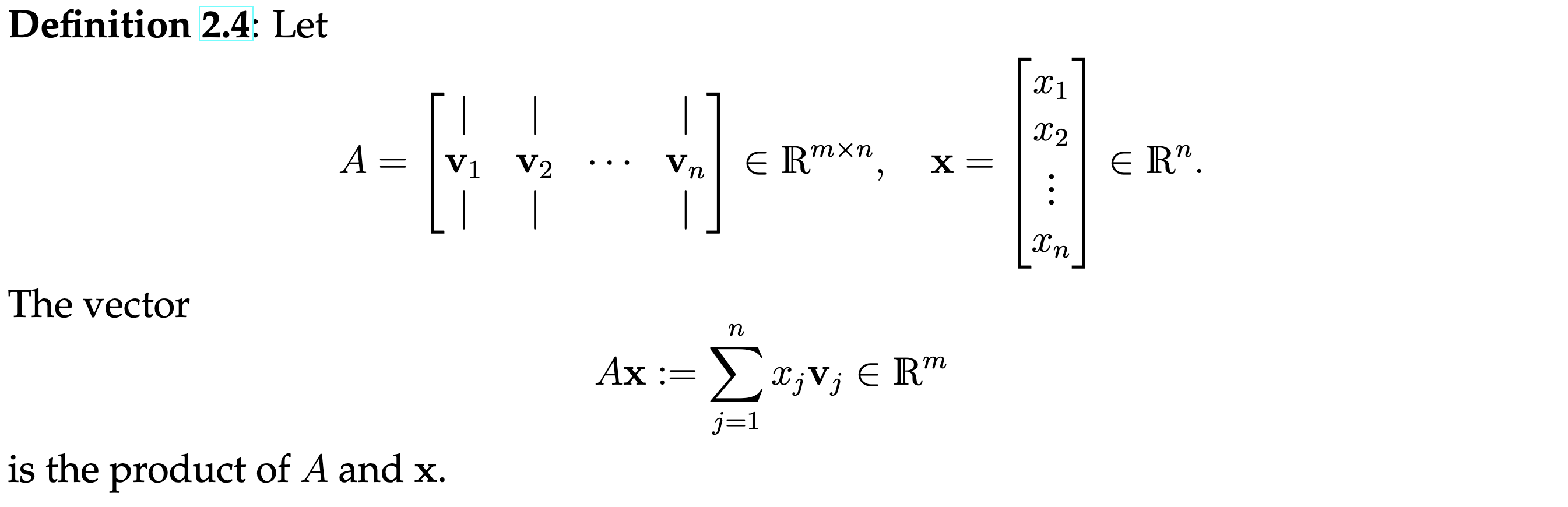
Row Definition

The row definition of matrix-vector multiplication highlights the operation performed by each row of the matrix on the vector, resulting in the components of the output vector.

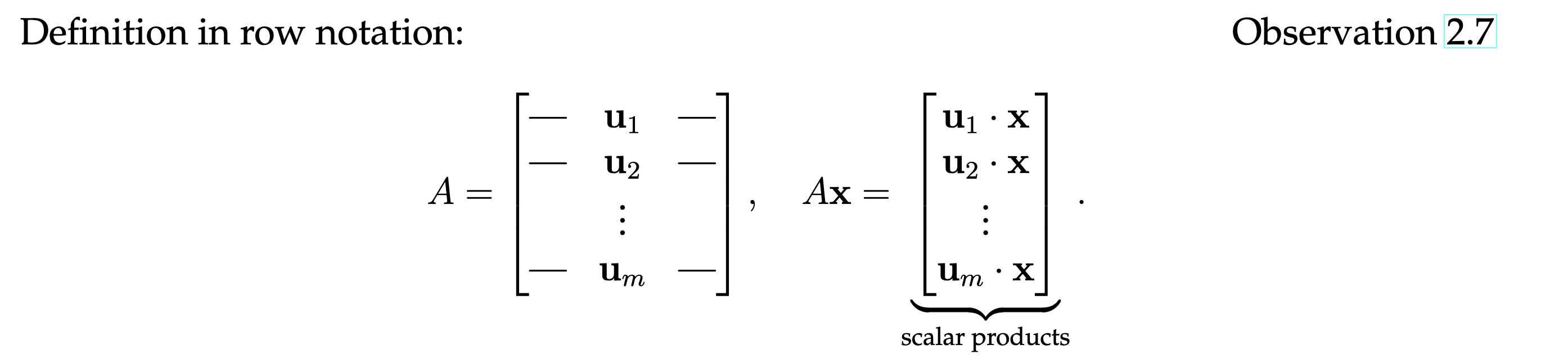
Direct Definition

The direct definition of matrix-vector multiplication provides a straightforward formulation of the operation, showing how each component of the resulting vector is calculated based on the elements of the matrix and the vector.

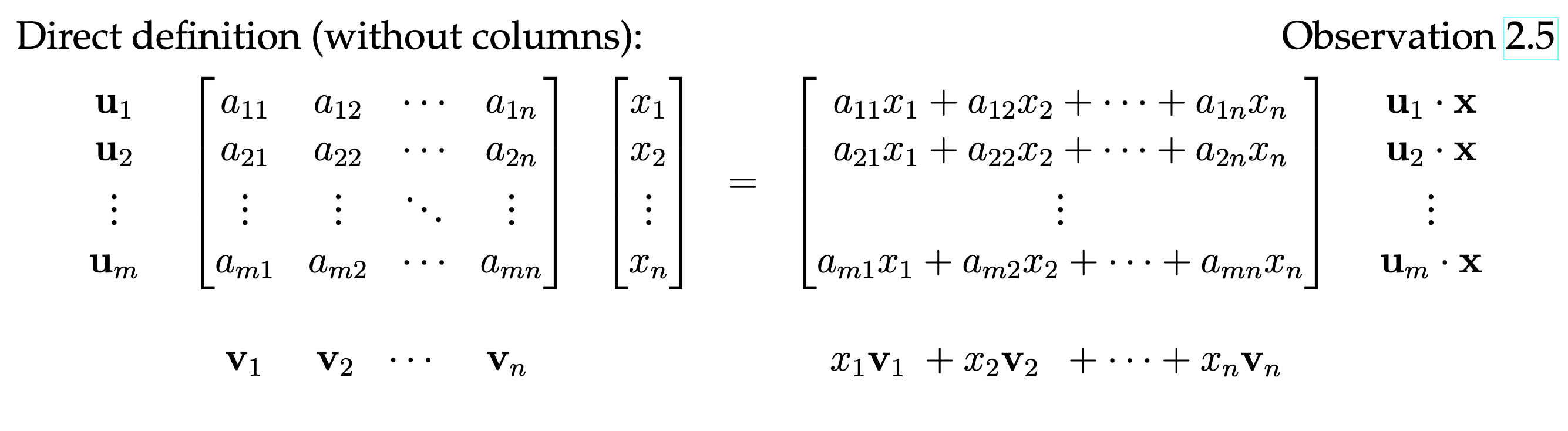
Column Space and Rank

Column Space

Let $A$ be an $m\times n$ matrix. The column space (Spaltenrang or Bild) of $A$ is defined as the span of its columns, denoted as $C(A)$:

$$C(A)=\{A\mathbf{x}:\mathbf{x}\in {\mathbb{R}}^n\}\subset {\mathbb{R}}^m$$

This represents all possible linear combinations of the columns of $A$ in ${\mathbb{R}}^m$.

Independent Columns

Independent columns refer to a set of columns in a matrix where no column can be expressed as a linear combination of the others. If a matrix has $k$ independent columns, it implies that those columns span a $k$-dimensional space.

Every linear combination of the columns is already a linear combination of the independent columns.

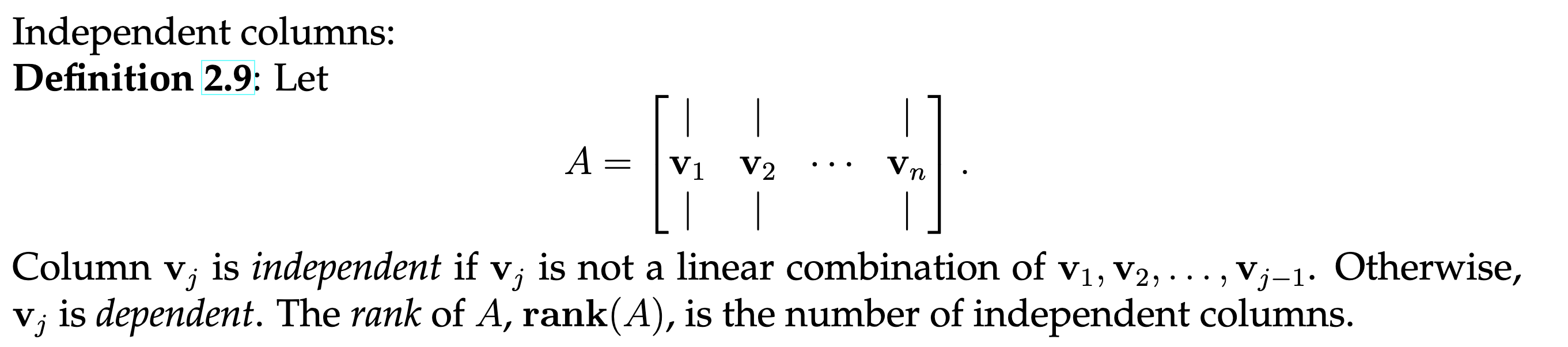
Rank

The rank (Rang) of a matrix $A$ is the dimension of its column space, which indicates the maximum number of linearly independent columns in $A$. In other words, it tells us how many dimensions are spanned by the columns of the matrix.

TLDR: The dimension of the column space is called the rank of the matrix.

Continue here: 05 Transpose and Multiplication