07 Equality, Ordered Pairs, Cartesian Product, Power Set and Relationships

Lecture from: 09.10.2024 | Video: Videos ETHZ

Set Equality

Two sets are considered equal if they have exactly the same elements. The order in which elements appear within a set doesn’t matter.

• Formal Definition: Sets $A$ and $B$ are equal, written as $A=B$, if and only if every element of $A$ is also an element of $B$, and vice versa.

• Example:

  • Set $A=\{1,2,3\}$
  • Set $B=\{3,1,2\}$

In this case, both sets contain the same elements (1, 2, and 3), just in a different order. Therefore, $A=B$.

Another way to look at this is: $A$ is a subset of $B$ and $B$ is a subset of $A$.

The Empty Set is a Subset of All Other Sets

Think of it this way: the empty set has no elements, so it can’t possibly contain an element that another set doesn’t have.

Proof by contradiction (Lemma 3.6):

Ordered Pairs

An ordered pair is a fundamental concept that establishes a specific relationship between two elements. Unlike sets, where order doesn’t matter, ordered pairs rely on the arrangement of their components.

Definition: An ordered pair $(a,b)$, often read as “a comma b,” consists of two elements a and b. The crucial aspect is that the element a comes first followed by b. This order defines the specific relationship represented by the pair.

Formally: $(a,b)$ is defined as the following set $\{\{a\},\{a,b\}\}$.

Cartesian Product

The Cartesian product is a fundamental operation that combines elements from two (or more) sets to create a new set of ordered pairs.

Formal Definition: Given two sets $A$ and $B$, their Cartesian product, denoted by $A\times B$, is the set of all possible ordered pairs $(a,b)$ where $a$ belongs to set $A$ and $b$ belongs to set $B$.

Mathematically: $A\times B=\{(a,b)|a\in A,b\in B\}$

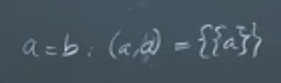
Cardinality: If $|A|=n$ and $|B|=m$, then $|A\times B|=n\times m$.

Example:

• Set $A=\{1,2\}$
• Set $B=\{a,b\}$

Then the Cartesian product $A\times B$ would be: $A\times B=\{(1,a),(1,b),(2,a),(2,b)\}$ $|A\times B|=2\times 2=4$

Another Example:

• Set $C=\{x,y\}$
• Set $D=\{1,2,3\}$

Then the Cartesian product $C\times D$ would be: $C\times D=\{(x,1),(x,2),(x,3),(y,1),(y,2),(y,3)\}$ $|C\times D|=2\times 3=6$

Relationship

A relationship, often denoted by the Greek letter $\rho$ (rho), is a fundamental concept that describes connections or associations between elements within sets. Formally, a relationship is defined as a subset of the Cartesian product of two sets. This also means that $\rho$ is a set containing ordered pairs.

Definition: Let $A$ and $B$ be two sets. A relationship $\rho$ from $A$ to $B$ is a subset of the Cartesian product $A\times B$. Symbolically:

$\rho \subseteq A\times B$

This means that a relationship $\rho$ consists of ordered pairs $(a,b)$ where $a$ belongs to set $A$ and $b$ belongs to set $B$. Each ordered pair in $\rho$ represents a specific connection or association between an element from $A$ and an element from $B$.

Power Set (Potenz Menge)

The power set of a set is the set of all possible subsets of that set, including the empty set and the set itself. Think of it as every combination you can make from the original elements.

• Symbol: We usually represent the power set of a set $A$ with the notation $\mathcal{P}(A)$ or $2^A$.
• Cardinality: If $|A|=n$, then $|\mathcal{P}(A)|=2^n$.

Example 1: Empty Set Let $A=\varnothing$. The power set of $A$ is: $\mathcal{P}(A)=\{\varnothing \}$. Note that the empty set is a subset of itself. $|\mathcal{P}(A)|=2^0=1$

Example 2: Set Containing the Empty Set Let $B=\{\varnothing \}$. The power set of $B$ is: $\mathcal{P}(B)=\{\varnothing ,\{\varnothing \}\}$. $|\mathcal{P}(B)|=2^1=2$

Example 3: A more typical set Let $C=\{1,2\}$. The power set of $C$ is: $\mathcal{P}(C)=\{\varnothing ,\{1\},\{2\},\{1,2\}\}$ $|\mathcal{P}(C)|=2^2=4$

Example 4: Let $D=\{a,b,c\}$. The power set of $D$ is: $\mathcal{P}(D)=\{\varnothing ,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\}$ $|\mathcal{P}(D)|=2^3=8$

Continue here: 08 Relations, Compositions and Properties