02 Star Search

Lecture from: 26.09.2024 | Video: Videos ETHZ | Rui Zhangs Notes | Official Script

Star Search

In many real-world systems like social networks or organizations, there can be a special individual called a star.

A star has two key traits:

Everyone knows the star
The star knows no one

Our task is simple: if there is a star in a group of $n$ people, we need to find them with the fewest possible questions. We can ask one person if they know another person.

It’s important to note that this “knowing” relation is not symmetric. If person $p_{1}$ knows person $p_{2}$ , it doesn’t mean that $p_{2}$ knows $p_{1}$ .

Algorithm 0: The Naive Way

The simplest way to solve this would be to ask each person about every other person. This means asking $n (n - 1)$ questions — too many!

Algorithm 1: Divide and Conquer

Instead of brute-forcing, we can use a more efficient approach inspired by recursion or divide-and-conquer (like we’ve seen in earlier algorithms).

How it works:

For $n \geq 3$ (since $n = 2$ is the base case), follow these steps:

Recursively find the star, $p_{s}$ , among the first $n - 1$ people.
Check if $p_{s}$ is the star among all $n$ people by:
1. Asking if $p_{s}$ is the star for the last person $p_{n}$ (just 2 questions).
2. If $p_{s}$ isn’t the star for $p_{n}$ , check if $p_{n}$ is the star among the first $n - 1$ people (ask $2 (n - 2)$ questions).

Best Case

The best scenario is when $p_{s}$ turns out to be the actual star in the group. This requires only 2 questions for each person, meaning we ask $2 (n - 1)$ questions in total.

Worst Case

In the worst case, $p_{s}$ isn’t the star, and we end up asking more questions in step 2.2. This could lead us back to the same amount of work as the naive algorithm, $n (n - 1)$ questions.

Algorithm 2: Avoid Excluding the Star

Can we improve the worst-case scenario? Yes!

In Algorithm 1, the worst case happens if we mistakenly exclude the real star during the recursive steps. We can avoid this by slightly modifying the approach:

Before running the recursion, check if the second last person, $p_{n - 1}$ , knows the last person $p_{n}$ . If they do, swap them out, since by definition they cannot be the star, and continue. This ensures we won’t accidentally exclude the star, i.e. the star is guaranteed to be part of the $n - 1$ people.
Once we reduce the group to two people, check if one of them is the star. If there’s no star, we’ll know for sure because our method guarantees the star, if it exists, remains in the group.

Worst-Case Scenario

In Algorithm 2, we make sure not to accidentally exclude the real star during the process. This improves the worst-case scenario compared to Algorithm 1, even though the general approach remains similar.

Here’s how it works:

Each time we check whether the current potential star, $p_{s}$ , is still the star for the newly added person $p_{n}$ , we need to ask 2 questions.
Additionally, before we proceed to the next recursive step, we make sure that the potential star is included in the next group of $n - 1$ people by asking 1 more question. This ensures we don’t exclude the real star.

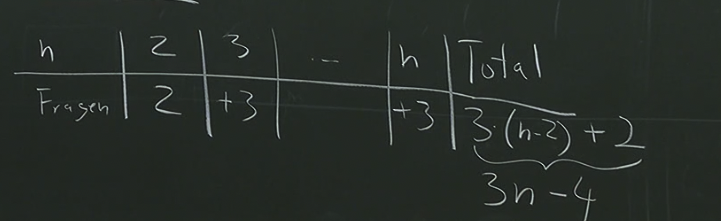
By summing up the total number of operations for the entire process, we find that the algorithm requires only $3 n - 4$ operations in the worst case — a significant improvement over the naive approach!

Note to self: we also did a bit of 1) Comparing Algorithms and 2) Asymptotic Notation.

Continue here: 03 Max Subarray Sum

CS Notes

Explorer