13 Vector Spaces, Bases, Dimension

Lecture from 30.10.2024 | Video: Videos ETHZ

Vector Spaces, Bases and Dimension

Our goal is to thoroughly understand how vector spaces are generated. A central concept in this pursuit is the basis, which represents a minimal set of linearly independent vectors capable of creating any other vector in the space through linear combinations.

Linear Combinations

Before we delve into bases, we must understand their fundamental components: linear combinations.

Linear Combination (Definition 4.13)

Let $V$ be a vector space and $G\subseteq V$ be a subset of vectors (potentially infinite). A linear combination of $G$ is a sum of the form:

$$\sum _{v\in F}{\lambda }_{v}v$$

where $F\subseteq G$ is a finite subset of $G$, and ${\lambda }_v\in \mathbb{R}$ for all $v\in F$. The restriction to a finite subset $F$ is crucial, as we’ll see later.

Example: Consider the set $G=\{v_1,v_2,v_3\}$. Valid linear combinations of $G$ include:

• $2v_1+3v_2-v_3$
• $v_1+5v_3$
• $v_1$

Closure under Linear Combinations (Lemma 4.14)

Let $V$ be a vector space and $G\subseteq V$. Every linear combination of $G$ remains within the vector space $V$.

Proof: We demonstrate this closure property using the axioms of a vector space and an inductive argument.

1. Setup: Consider a finite subset $F=\{v_1,...,v_n\}$ of $G$ and a general linear combination:

   $$\sum _{j=1}^n{\lambda }_j{v}_j$$

2. Scalar Multiplication: By the definition of a vector space, scalar multiplication is a closed operation within $V$. Thus, for each $j=1,...,n$, the product $w_j={\lambda }_j{v}_j$ is also a vector in $V$.

3. Closure under Addition: Vector spaces are closed under addition. Consequently, the sum of any two vectors in $V$, such as $w_1$ and $w_2$, will also reside in $V$.

4. Induction: We use induction to generalize this to any finite sum.

   • Base Case (n=1): A linear combination of a single vector, $w_1={\lambda }_1{v}_1$, is in $V$ (from step 2).
   • Inductive Step: Assume that the sum of $k$ vectors, $w=w_1+...+w_k$, is in $V$. We need to show that adding the $(k+1)$-th vector, $w_{k+1}$, also results in a vector in $V$. By closure under addition (step 3), since $w\in V$ and $w_{k+1}\in V$, their sum $w+w_{k+1}$ is also in $V$.

5. Conclusion: By induction, any finite linear combination of vectors from $F$ (and therefore, from any finite subset of $G$) remains within $V$.

Why Infinite Linear Combinations Can Fail:

The previous lemma specifically addresses finite linear combinations. Infinite linear combinations may produce results that lie outside the original vector space.

Example: Consider the vector space $V$ of polynomials with real coefficients in one variable $x$. While each individual monomial ($1,x,x^2,x^3,...$) belongs to $V$, the infinite sum:

$$\sum _{i=0}^{\infty }{x}^i=\frac{1}{1-x}$$

converges to a rational function (for $|x|<1$), which is not a polynomial and therefore not in $V$.

This emphasizes the importance of restricting our discussion to finite linear combinations when defining spans and bases.

Span and Linear Independence: Key Concepts

Definition 4.15 (Span and Linear Independence): Let $V$ be a vector space and $G\subseteq V$.

• Span($G$): The set of all possible finite linear combinations of vectors in $G$. Formally:

  $$\text{Span}(G)=\left\{\sum _{v\in F}{\lambda }_{v}v\mid {\lambda }_v\in \mathbb{R}\text{ for all }v\in F,F\subseteq G\text{ finite}\right\}$$

• Linear Independence: $G$ is linearly independent if no vector $v\in G$ can be expressed as a linear combination of the other vectors in $G\setminus \{v\}$. Equivalently, $G$ is linearly independent if the only way to obtain the zero vector as a linear combination of vectors in $G$ is by setting all coefficients ${\lambda }_v$ to zero.

• Linear Dependence: $G$ is linearly dependent if at least one vector $w\in G$ can be expressed as a linear combination of the other vectors in $G\setminus \{w\}$.

See: 03 Linear Dependence and Independence for more info.

Basis: A Minimal Generating Set

Basis (Definition 4.16)

A subset $B\subseteq V$ is a basis for vector space $V$ if:

1. $B$ is linearly independent.
2. Span($B$) = $V$ (every vector in $V$ is a linear combination of vectors in $B$).

A basis provides a minimal and efficient way to represent every vector in the vector space.

Bases in ℝᵐ (Observation 4.18):

Any set of $m$ linearly independent vectors in ${\mathbb{R}}^m$ forms a basis for ${\mathbb{R}}^m$. This is a direct consequence of Theorem 3.11 (the Inverse Theorem, see Inverse Theorem (Theorem 3.11)), which states that a square matrix with linearly independent columns is invertible.

If we form a matrix $A$ whose columns are our $m$ linearly independent vectors, then for any vector $v\in {\mathbb{R}}^m$, the equation $Ax=v$ has a unique solution $x\in {\mathbb{R}}^m$. This solution $x$ provides the coefficients for expressing $v$ as a linear combination of the columns of $A$ (i.e., our original $m$ vectors). Thus, these $m$ vectors span ${\mathbb{R}}^m$ and, being linearly independent, form a basis.

The Steinitz Exchange Lemma: A Foundation for Dimension (Lemma 4.19)

The Steinitz Exchange Lemma is a crucial result that connects linearly independent sets and spanning sets in a vector space. It’s essential for understanding the concept of dimension.

Note for readers: Here is a video explaining the content in a much better way IMO.

Let $V$ be a vector space, $F\subseteq V$ a finite, linearly independent set, and $G\subseteq V$ a finite spanning set (i.e., Span($G$) = $V$). Then:

1. $|F|\le |G|$.
2. There exists a subset $E\subseteq G$ with $|E|=|G|-|F|$ such that Span($F\cup E$) = $V$. (Note: $E$ can contain elements of $F$).

Proof (by Induction on |F|):

• Base Case (|F| = 0):

  1. $0\le |G|$ is trivially true.
  2. Choose $E=G$. Then Span($F\cup E$) = Span($\varnothing \cup G$) = Span($G$) = $V$.

• Inductive Hypothesis: Assume the lemma holds for any linearly independent set $F$ with $|F|<k$.

• Inductive Step (|F| = k):

  1. Choose and Remove: Select any $u\in F$ and let $F^{\prime }=F\setminus \{u\}$. $F^{\prime }$ remains linearly independent.

  2. Apply Hypothesis: Since $|F^{\prime }|<k$, the inductive hypothesis applies:

     • $|F^{\prime }|\le |G|$.
     • There exists $E^{\prime }\subseteq G$ with $|E^{\prime }|=|G|-|F^{\prime }|$ such that Span($F^{\prime }\cup E^{\prime }$) = $V$.

  3. Express u: Since $F^{\prime }\cup E^{\prime }$ spans $V$, we can write $u$ as a linear combination: $u={\sum }_{v\in F^{\prime }\cup E^{\prime }}{\lambda }_{v}v$ Since $F$ is linearly independent, $u$ cannot be expressed solely using vectors from $F^{\prime }$ (otherwise, it would be a linear combination of the other vectors in F). Therefore, at least one ${\lambda }_w\ne 0$ for some $w\in E^{\prime }$.

  4. Exchange: Choose such a $w$ with ${\lambda }_w\ne 0$. Let $E=E^{\prime }\setminus \{w\}$. Now, $|E|=|E^{\prime }|-1=(|G|-|F^{\prime }|)-1=|G|-(|F|-1)-1=|G|-|F|$.

  5. Show Spanning: We need to prove Span($F\cup E$) = $V$.

     • From the equation for $u$ above, since ${\lambda }_w\ne 0$, we can rearrange to express $w$ as a linear combination of $u$ and vectors in $F^{\prime }\cup E$. This means $w\in$ Span($F\cup E$).
     • Any vector $v\in V$ can be expressed using vectors in $F^{\prime }\cup E^{\prime }$. We can substitute the expression for $w$ in terms of $F\cup E$ into the representation for $v$. This shows that $v$ can be expressed using only vectors from $F\cup E$, and therefore Span($F\cup E$) = $V$.

This completes the induction, proving the Steinitz Exchange Lemma.

Uniqueness of Basis Size and Dimension

Theorem 4.20 (Uniqueness of Basis Size): Let $V$ be a finitely generated vector space. If $B$ and $B^{\prime }$ are both finite bases for $V$, then $|B|=|B^{\prime }|$.

Proof: Apply the Steinitz Exchange Lemma twice:

1. With $F=B$ and $G=B^{\prime }$, we get $|B|\le |B^{\prime }|$.
2. With $F=B^{\prime }$ and $G=B$, we get $|B^{\prime }|\le |B|$. Therefore, $|B|=|B^{\prime }|$.

Definition 4.23 (Dimension): The dimension of a finitely generated vector space $V$, denoted dim($V$), is the number of vectors in any basis for $V$. (Note: dim(${\mathbb{R}}^m$) = $m$).

Existence of a Basis: Simplified Basis Criterion (Lemma 4.24)

Let $V$ be a vector space with dim($V$) = $d$.

1. If $F\subseteq V$ contains $d$ linearly independent vectors, then $F$ is a basis for $V$.
2. If $G\subseteq V$ contains $d$ vectors and Span($G$) = $V$, then $G$ is a basis for $V$.

Proof:

1. Let $B$ be a basis for $V$ (so $|B|=d$). Apply the Steinitz Exchange Lemma with $F$ and $B$. Since $|F|=|B|=d$, the exchange set $E$ is empty. Thus, Span($F$) = Span($F\cup E$) = Span($F\cup \varnothing$) = $V$, so $F$ is a basis.
2. By Theorem 4.22, there exists a basis $B\subseteq G$ with $|B|=d$. Since $|G|=d$ as well, we must have $B=G$, meaning $G$ itself is a basis.

This lemma simplifies checking if a set of vectors forms a basis: If the set has the correct number of vectors (equal to the dimension), then we only need to verify either linear independence or that it spans the space.

Example: The Vector Space of Polynomials in n Variables

Let’s explore a specific example of a vector space: the set of all polynomials in n variables with a degree at most d. This will illustrate the concepts of basis and dimension in a more concrete setting.

Note for readers: In this part the professor rushed through quite quickly and it was quite confusing, I’ve no clue if this part here is correct and makes sense. If you find a mistake let me know in the comments, or write me an email ¯\_(ツ)_/¯

Definitions (Monomial, Degree, Polynomial)

• A monomial in n variables is an expression of the form: $x^f=x_1^{f_1}{x}_2^{f_2}\dots x_n^{f_n}$ where $f=(f_1,f_2,...,f_n)\in (\mathbb{N}\cup \{0\}{)}^n$ is a vector of non-negative integer exponents.

  Example:

  • In two variables, $x^2{y}^3$ is a monomial with $f=(2,3)$
  • In three variables, $x^1{y}^0{z}^2$ is a monomial with $f=(1,0,2)$

• The degree of a monomial $x^f$ is the sum of its exponents: $\text{degree}(x^f)={\sum }_{i=1}^n{f}_i$ Example:

  • The degree of $x^2{y}^3$ is $2+3=5$.
  • The degree of $x^1{y}^0{z}^2$ is $1+0+2=3$.

• A polynomial $p(x)$ in n variables of degree at most d is a real linear combination of monomials with degrees up to d. Formally: $p(x)={\sum }_{f\in S_d}{a}_f{x}^f$ where $a_f\in \mathbb{R}$ are the coefficients, and $S_d$ is the set of all possible exponent vectors $f$ such that the degree is at most d: $S_d=\left\{f\in (\mathbb{N}\cup \{0\}{)}^n\mid {\sum }_{i=1}^n{f}_i\le d\right\}$

  Example:

  • A polynomial in two variables (x and y) of degree at most 2 could look like: $3x^2+2xy-5y^2+7x-y+1$.

Operations on Polynomials:

We define addition and scalar multiplication on polynomials as follows:

• For $p(x)={\sum }_{f\in S_d}{a}_f{x}^f$ and $q(x)={\sum }_{f\in S_d}{b}_f{x}^f$, and a scalar $\lambda \in \mathbb{R}$:
  • Scalar Multiplication: $\lambda p(x)={\sum }_{f\in S_d}(\lambda a_f)x^f$ Example: If $p(x)=2x^2+3xy-y^2$ and $\lambda =4$, then $\lambda p(x)=8x^2+12xy-4y^2$.
  • Addition: $p(x)+q(x)={\sum }_{f\in S_d}(a_f+b_f)x^f$ Example: If $p(x)=2x^2+3xy-y^2$ and $q(x)=x^2-2xy+5y^2$, then $p(x)+q(x)=3x^2+xy+4y^2$.

Vector Space of Polynomials

The set of all polynomials in n variables of degree at most d, denoted by $\mathbb{R}[x_1,...,x_n{]}_{\le d}$, is a vector space of dimension $|S_d|$.

Proof:

1. Monomials as a Basis: The set of all monomials $\{x^f\mid f\in S_d\}$ forms a basis for $\mathbb{R}[x_1,...,x_n{]}_{\le d}$. This is because:

   • Spanning: By definition, every polynomial in $\mathbb{R}[x_1,...,x_n{]}_{\le d}$ is a linear combination of these monomials. Example:

     • In two variables (x and y) with degree at most 2, we can take the set of monomials: $\{1,x,y,x^2,xy,y^2\}$. Any polynomial with degree at most 2 can be formed by a linear combination of these monomials.

   • Linear Independence: No monomial in the set can be expressed as a linear combination of the other monomials. This can be seen by considering the unique combination of exponents in each monomial. Example:

     • Consider the monomials $x^2$ and $xy$. The exponent vectors are $(2,0)$ and $(1,1)$, respectively. There is no way to combine $xy$ with other monomials (like 1, $x$, or $y$) to get $x^2$ because they have different exponent vectors.

2. Dimension: Since the set of monomials $\{x^f\mid f\in S_d\}$ is a basis, the dimension of the vector space $\mathbb{R}[x_1,...,x_n{]}_{\le d}$ is equal to the number of elements in this basis, which is $|S_d|$. Example:

   • Consider polynomials in two variables (x and y) with degree at most 2. $S_2=\{(0,0),(1,0),(0,1),(2,0),(1,1),(0,2)\}$. Therefore, $|S_2|=6$, and the dimension of this space of polynomials is 6.

     Visual example:

     

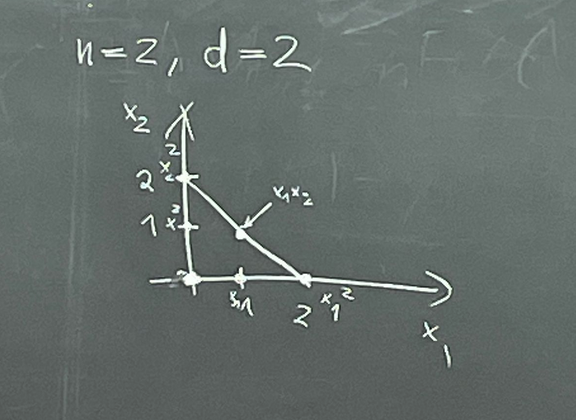
Therefore, $\text{dim}(\mathbb{R}[x_1,...,x_n{]}_{\le d})=|S_d|$.

This example demonstrates how the concepts of basis and dimension apply to a specific, infinite-dimensional vector space. Note that even though the vector space itself is infinite-dimensional if we allow any degree, once we constrain the space by limiting the maximum degree to d, the resulting subspace is finite-dimensional.

The choice of a basis—in this case, the monomials—provides a structured and manageable way to work with these polynomials, and the dimension tells us how many “degrees of freedom” we have when constructing polynomials within this space.

Continue here: 14 Fundamental Subspaces, Column Space, Row Space, Nullspace