12 Cardinality, Number Theory, Rings, Euclidian Rings, Ideal, Congruence, Modular Arithmetic, Diophantine Equations

Lecture from: 28.10.2024 | Video: Videos ETHZ

The Cardinality of $\mathbb{R}$ and $\mathbb{R}\times \mathbb{R}$

It might seem intuitive, at first glance, that $\mathbb{R}$ should have strictly smaller cardinality than $\mathbb{R}\times \mathbb{R}$. After all, $\mathbb{R}\times \mathbb{R}$ represents the entire 2D plane, while $\mathbb{R}$ represents a single line. How could we possibly map all the points in the plane onto a line without losing some information? This suggests that there should be an injection from $\mathbb{R}\times \mathbb{R}$ to $\mathbb{R}$ but no bijection.

However, this intuition is misleading! The Cantor-Bernstein-Schroeder Theorem tells us that if we can find an injection from $\mathbb{R}$ to $\mathbb{R}\times \mathbb{R}$ and an injection from $\mathbb{R}\times \mathbb{R}$ to $\mathbb{R}$, then $\mathbb{R}$ and $\mathbb{R}\times \mathbb{R}$ must have the same cardinality.

Demonstrating Equivalence via Binary Representations

A more concrete way to see this is to consider the binary representations of real numbers and pairs of real numbers. We know that the set of all infinite binary sequences $\{0,1{\}}^{\infty }$ is equivalent to the set of real numbers $\mathbb{R}$. (see [[11 Functions, Relations, Cardinality, Countability, Cantor’s Diagonalization Argument#The Uncountability of Infinite Binary Sequences (Cantor’s Diagonalization Argument)#Uncountability of Real Numbers]])

• Interleaving: Given two infinite binary sequences, we can interleave their bits to create a single infinite binary sequence. For example, from the sequences (01101…) and (10010…), we can construct (011001110…). This process is easily reversible, meaning we can recover the original sequences.
• Bijection: This interleaving process defines a bijection between $\{0,1{\}}^{\infty }\times \{0,1{\}}^{\infty }$ and $\{0,1{\}}^{\infty }$.
• Extension to Higher Dimensions: This same interleaving technique can be generalized to higher dimensions. We can create a bijection between $\{0,1{\}}^{\infty }\times \{0,1{\}}^{\infty }\times ...\times \{0,1{\}}^{\infty }$ (representing ${\mathbb{R}}^n$) and $\{0,1{\}}^{\infty }$ (representing $\mathbb{R}$).

Cardinality of Power Sets

Another interesting and counterintuitive result is that for any set $A$, the power set of $A$, denoted by $P(A)$ (the set of all subsets of $A$), always has a strictly larger cardinality than $A$ itself, meaning $A\prec P(A)$. This is known as Cantor’s Theorem. This theorem has significant implications for understanding the hierarchy of infinite sets. It tells us that there are infinitely many different levels of infinity.

Number Theory

Number theory delves into the properties and relationships of integers, exploring topics like prime numbers, divisibility, factorization, and congruences. In our exploration, we’ll primarily work with the set of integers, denoted by $\mathbb{Z}$. A rigorous approach to number theory would involve building the number system from foundational axioms like the Peano axioms. However, for this course, we’ll assume a basic understanding of integer properties.

Divisibility and Its Properties

Definition (Divisibility): An integer a divides an integer b, denoted $a|b$, if there exists an integer k such that $b=ak$.

Example: $3|12$ because $12=3\cdot 4$. However, $5\nmid 12$ because there’s no integer k such that $12=5k$.

Property: If $a|b$ and $a|c$, then $a|(b+c)$.

Proof:

1. Assumptions: Given $a|b$ and $a|c$, there exist integers $k_1$ and $k_2$ such that $b=a{k}_1$ and $c=a{k}_2$.
2. Adding and Factoring: Adding these equations, we have $b+c=a{k}_1+a{k}_2$. Using the distributive property, we can factor out a: $b+c=a(k_1+k_2)$.
3. Conclusion: Since the sum of integers is an integer, $k_1+k_2$ is an integer. Thus, $b+c$ can be expressed as a multiple of a. Therefore, $a|(b+c)$.

Generalizing Beyond Integers: The Concept of a Ring

The proof above relies on properties like distribution and the closure of integers under addition and multiplication. These properties aren’t unique to integers; they hold in other algebraic structures as well. This observation leads us to a more abstract and general concept: the ring.

Rings: A General Algebraic Structure

A ring is a set R equipped with two binary operations, addition ($+$) and multiplication ($\cdot$), along with two special elements, 0 and 1, that satisfy specific axioms. Formally, a ring $(R,+,\cdot ,0,1)$ is defined by the following axioms:

Axioms of Addition:

• Associativity: For all $a,b,c\in R$, $(a+b)+c=a+(b+c)$.
• Commutativity: For all $a,b\in R$, $a+b=b+a$.
• Identity Element (Zero): There exists an element $0\in R$ such that for all $a\in R$, $a+0=0+a=a$.
• Additive Inverse: For all $a\in R$, there exists an element $-a\in R$ such that $a+(-a)=(-a)+a=0$.

Axioms of Multiplication:

• Associativity: For all $a,b,c\in R$, $(a\cdot b)\cdot c=a\cdot (b\cdot c)$.
• Identity Element (One): There exists an element $1\in R$ such that for all $a\in R$, $a\cdot 1=1\cdot a=a$.

Distributive Laws (connecting addition and multiplication):

• For all $a,b,c\in R$, $a\cdot (b+c)=(a\cdot b)+(a\cdot c)$.
• For all $a,b,c\in R$, $(a+b)\cdot c=(a\cdot c)+(b\cdot c)$.

Examples of Rings:

• Integers ($\mathbb{Z}$): The set of integers with standard addition and multiplication forms a ring.
• Real Numbers ($\mathbb{R}$): The set of real numbers with standard addition and multiplication forms a ring.
• Matrices: The set of $n\times n$ matrices with matrix addition and multiplication forms a ring.
• Polynomials: The set of polynomials with coefficients in a given ring forms a ring.

The concept of a ring allows us to generalize properties and theorems from number theory to a much broader context. Any result that depends only on the ring axioms will hold true in any ring, not just integers. For example, since integers form a ring, the property of divisibility we proved earlier ($a|b$ and $a|c$ imply $a|(b+c)$) is also applicable to any ring structure under similar conditions.

Proving $a\cdot 0=0$ in a Ring

While seemingly obvious, the property that any element multiplied by zero results in zero ($a\cdot 0=0$) is not explicitly stated in the ring axioms. Therefore, we must prove it using the axioms.

1. Additive Identity: We know that for any element $b$ in a ring, $b=0+b$, where 0 is the additive identity. We can apply this to $a\cdot 0$: $a\cdot 0=0+a\cdot 0$
2. Additive Inverse: For every element $a\cdot 0$, there exists an additive inverse $-(a\cdot 0)$ such that $-(a\cdot 0)+(a\cdot 0)=0$. We add this inverse to both sides of our equation: $-(a\cdot 0)+a\cdot 0=-(a\cdot 0)+0+a\cdot 0$ $0=-(a\cdot 0)+a\cdot 0$
3. Zero as a Sum: The additive identity, 0, can be expressed as 0 + 0. We substitute this into our original equation: $a\cdot 0=0+a\cdot 0$ $a\cdot 0=(0+0)+a\cdot 0$
4. Associativity of Addition and Distributivity: We can rewrite the equation using associativity: $a\cdot 0=0+(0+a\cdot 0)$ $a\cdot 0=0+a\cdot (0+0)$ Then, we can use the distributive property: $a\cdot 0=0+(a\cdot 0)$ This shows we effectively swapped the two zeros by applying associativity and distributivity and then the property that $0+0=0$.
5. Adding the Inverse: From step two, we already know that: $0=-(a\cdot 0)+(a\cdot 0)$ The left side is $a\cdot 0$ from the previous step and the right side is $0$ so: $a\cdot 0=0$ Therefore, we have proven that $a\cdot 0=0$ for any element a in a ring. This demonstrates how we can derive important properties using the fundamental axioms of a ring.

Example: Gaussian Integers ($\mathbb{Z}[i]$)

Gaussian integers are a subset of complex numbers. They extend the concept of integers to the complex plane. Instead of just having integers along the real number line, Gaussian integers form a grid of points in the complex plane.

Definition: The set of Gaussian integers, denoted by $\mathbb{Z}[i]$, is defined as:

$\mathbb{Z}[i]=\{a+bi\mid a,b\in \mathbb{Z}\}$

where i is the imaginary unit ($i^2=-1$), and a and b are integers. The integer a is called the real part, and the integer b is called the imaginary part of the Gaussian integer $a+bi$.

Multiplication of Gaussian Integers:

The multiplication of two Gaussian integers $(a+bi)$ and $(c+di)$ is performed using the distributive property and the fact that $i^2=-1$:

\begin{align*} (a + bi)(c + di) &= a(c + di) + bi(c + di) \\ &= ac + adi + bci + bdi^2 \\ &= ac + adi + bci - bd \\ &= (ac - bd) + (ad + bc)i \end{align*}

Gaussian Integers as a Ring: The set of Gaussian integers $\mathbb{Z}[i]$ forms a ring under the standard complex addition and multiplication operations. This means that it satisfies all the ring axioms described earlier. The additive identity is $0=0+0i$, and the multiplicative identity is $1=1+0i$.

The Euclidean Theorem (Theorem 4.1)

The Euclidean Theorem, a fundamental result in number theory, establishes that given any two integers a (the dividend) and d (the divisor), where d is not zero, we can uniquely express a as the product of d and a quotient q, plus a remainder r.

Theorem 4.1 (Euclid): For all integers a and d ($d\ne 0$), there exist unique integers q and r such that: $a=dq+r\text{and}0\le r<|d|$

Here:

• a is the dividend.
• d is the divisor.
• q is the quotient.
• r is the remainder, often denoted as $R_d(a)$ or $a\mathrm{mod}d$.

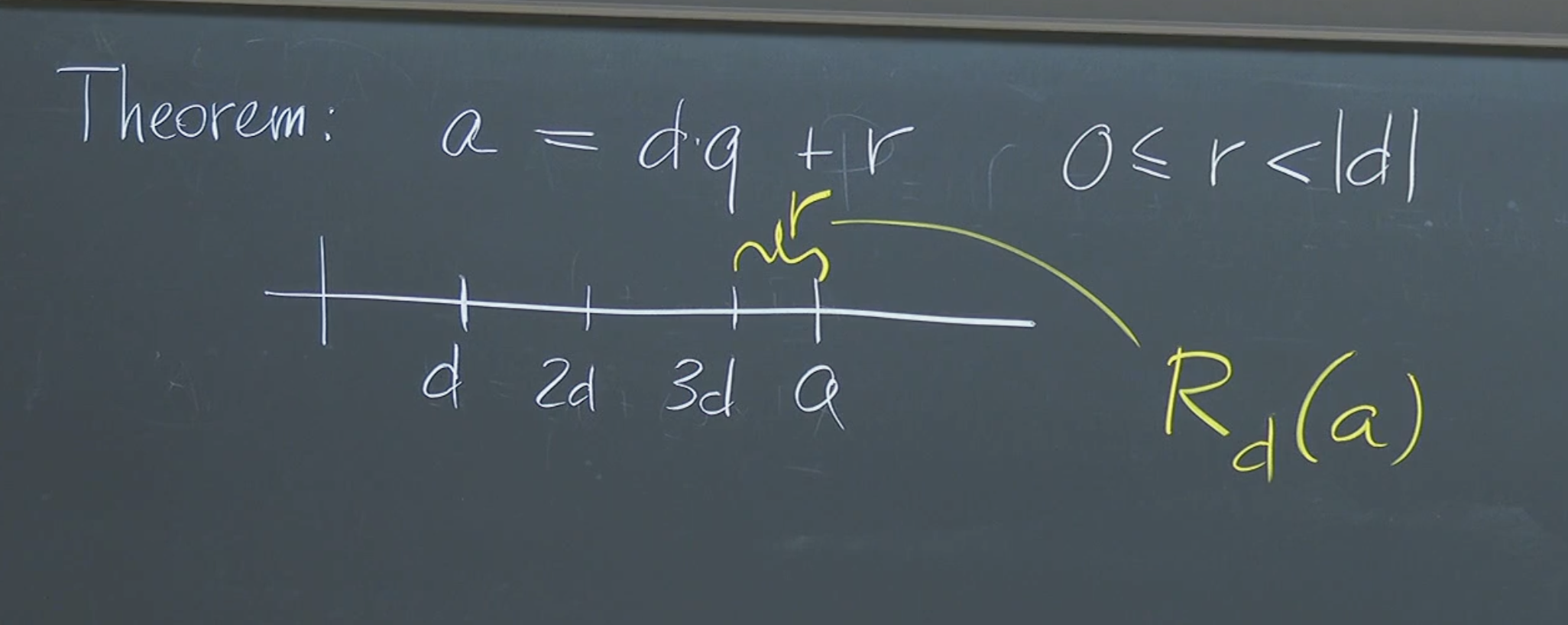
Proof: Check this proof or look at the script.

Euclidean Rings

Building upon the concept of rings and the Euclidean Theorem for integers, we now introduce Euclidean rings. These rings possess a division algorithm similar to integers, allowing us to perform division with remainder.

Definition

A Euclidean ring is a commutative ring R together with a function $N:R\setminus \{0\}\to \mathbb{N}\cup \{0\}$ called a Euclidean function or norm that satisfies the following two properties:

1. Division with Remainder: For all $a,b\in R$ with $b\ne 0$, there exist $q,r\in R$ such that: $a=bq+r$ and either $r=0$ or $N(r)<N(b)$. Here, q is called the quotient, and r is called the remainder.
2. Norm Comparison: For all $a,b\in R$ where $a,b\ne 0$, $N(a)\le N(ab)$.

Explanation:

• Euclidean Function (Norm): The Euclidean function N maps non-zero elements of the ring to non-negative integers. It provides a way to measure the “size” of elements in the ring. The specific definition of N can vary depending on the ring.

• Connection to the Euclidean Theorem: The first property directly generalizes the Euclidean Theorem for integers. It guarantees that we can perform division with remainder, where the remainder is either zero or “smaller” than the divisor (as measured by the Euclidean function).

• Not all rings are Euclidean: It’s important to note that not all commutative rings are Euclidean rings. The existence of a Euclidean function is a special property.

Examples:

• Integers ($\mathbb{Z}$): The integers form a Euclidean ring with the absolute value function as the Euclidean function: $N(a)=|a|$.
• Gaussian Integers ($\mathbb{Z}[i]$): The Gaussian integers form a Euclidean ring with the norm function defined as $N(a+bi)=a^2+b^2$.

Unique Prime Factorization and the Fundamental Theorem of Arithmetic

The Euclidean property, which guarantees the existence of a division algorithm, is the underlying reason why the Fundamental Theorem of Arithmetic holds. This theorem states that every integer greater than 1 can be uniquely factored into a product of prime numbers (up to the order of the factors).

Fundamental Theorem of Arithmetic: Every integer $n>1$ can be represented uniquely as a product of prime numbers:

$n=p_1^{e_1}{p}_2^{e_2}\dots p_k^{e_k}$

where $p_1,p_2,...,p_k$ are distinct prime numbers, and $e_1,e_2,...,e_k$ are positive integers. Uniqueness means that the prime factors and their exponents are uniquely determined by n (except for the order in which they appear).

Greatest Common Divisors

The concept of a greatest common divisor (GCD) is fundamental in number theory and extends to more general structures (e.g., polynomial rings) than just integers. It helps us understand the divisibility relationships between numbers.

Definition: For integers a and b (not both 0), an integer d is called a greatest common divisor of a and b if:

1. Divisibility: d divides both a and b, meaning $d|a$ and $d|b$.
2. Maximality: For every common divisor c of a and b, we have $c|d$. In other words, d is divisible by every other common divisor of a and b.

Key Points:

• Not Just the Largest: The term “greatest” in GCD refers to the divisibility relation, not the standard ordering of integers (less than or equal to). While the GCD is typically the largest common divisor, it’s the maximality in terms of divisibility that’s crucial.

• Multiple Greatest Common Divisors: In general, there may be multiple greatest common divisors for a given pair of integers a and b. However, they differ only by a unit (either 1 or -1). For example, for integers, both 3 and -3 are GCDs of 12 and 9.

Notation: The greatest common divisor of a and b is denoted as $\text{gcd}(a,b)$ and usually refers to the positive of the greatest common divisors.

Lemma: $\text{gcd}(m,n-qm)=\text{gcd}(m,n)$

Lemma 4.2: For any integers m, n, and q, we have

$\text{gcd}(m,n-qm)=\text{gcd}(m,n)$

which implies: $\text{gcd}(m,R_m(n))=\text{gcd}(m,n)$

Proof

We will demonstrate that every common divisor of m and $n-qm$ is also a common divisor of m and n, and vice versa. This implies that the sets of common divisors of these two pairs are the same, and therefore their greatest common divisors are also equal.

1. Common Divisor of m and n - qm $⟹$ Common Divisor of m and n:

Let d be a common divisor of m and $n-qm$. This means that $d|m$ and $d|(n-qm)$. Since $d|m$, we can write $m=dk$ for some integer k. Since $d|(n-qm)$, we can write $n-qm=dl$ for some integer l. Now, we can add $qm$ to both sides of this equation:

$n=dl+qm=d(l+kq)$

Since $l+kq$ is an integer, we have shown that $d|n$. Thus, d is a common divisor of m and n.

2. Common Divisor of m and n $⟹$ Common Divisor of m and n - qm:

Let d be a common divisor of m and n. This means $d|m$ and $d|n$. Since $d|m$, we have $m=dk$ for some integer k. Since $d|n$, we have $n=dl$ for some integer l. Subtracting $qm$ from both sides, we get:

$n-qm=dl-qm=d(l-qk)$

Since $l-qk$ is an integer, we have shown that $d|(n-qm)$. Thus, d is a common divisor of m and $n-qm$.

Conclusion:

We have shown that any common divisor of m and $n-qm$ is also a common divisor of m and n, and vice versa. Therefore, the greatest common divisors of these two pairs must be the same:

$\text{gcd}(m,n-qm)=\text{gcd}(m,n)$

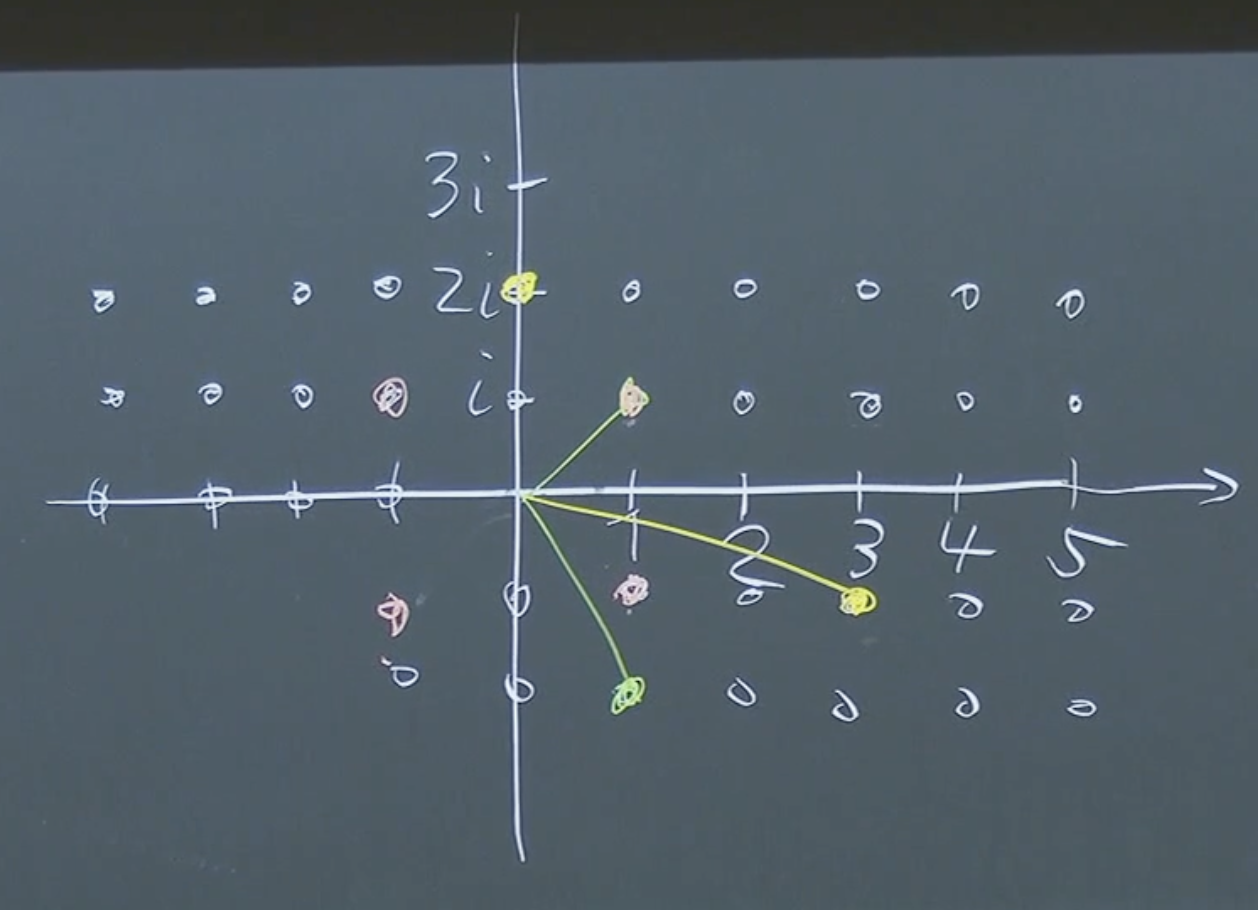
In $\mathbb{Z}[i]$ we can have up to 4 unique $gcd$ which are all symmetric (red dots in picture below).

Ideal $(a,b)$

Definition: The ideal generated by elements a and b in R, denoted by $(a,b)$, is the set of all linear combinations of a and b with coefficients from R:

$(a,b)=\{ua+vb\mid u,v\in R\}$

Consider the ring of integers, $\mathbb{Z}$. The ideal generated by 2 and 3, denoted $(2,3)$, is the set of all integers that can be expressed as a linear combination of 2 and 3. This set is: $(10,16)=\{0,10,16,26,6,4,2,\dots \}=(2)$

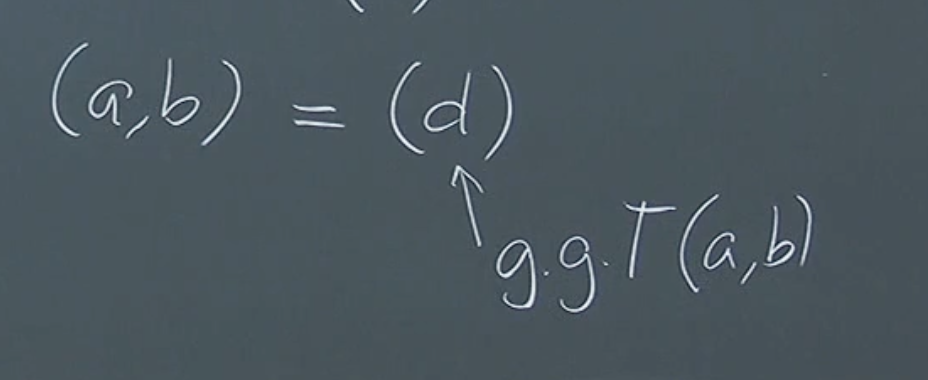
Every ideal can be generated by a single element is called a Principal Ideal Domain (PID). Additionally this element happens to also be the $gcd$ of it’s previous elements.

Corollary: $gcd(a,b)=ua+vb$

This is an important corollary that has applications in cryptography, particularly in the RSA algorithm. The result follows directly from the concept of ideals.

Explanation:

In the ring of integers, the ideal $(a,b)$ can be generated by a single element, which is the greatest common divisor of a and b (i.e., $gcd(a,b)$). Since the ideal is generated by this single element, we can express any element in the ideal as a linear combination of a and b. Therefore, the GCD can also be expressed as a linear combination of a and b: $gcd(a,b)=ua+vb$ for some integers u and v.

Example:

In the example of $(17,7)$, the GCD is 1. We can find integers u and v that satisfy $gcd(2,3)=ua+vb$. For example, $u=-2$ and $v=5$ give us $1=-2\cdot 17+5\cdot 7$.

Congruences and Modular Arithmetic: Exploring Remainders and Patterns

This section explores congruences and modular arithmetic, where we focus on the remainders when integers are divided by a specific number (the modulus). These concepts allow us to study patterns and relationships between integers in a new way.

Example

Let’s consider the product $293843846\cdot 231412331$. Without performing the actual multiplication, we can tell that the result is even. This is because we know that if at least one of the numbers in a product is even, the product must be even.

The key idea here is that the evenness or oddness of a number is determined by its remainder when divided by 2. An even number leaves a remainder of 0 when divided by 2, while an odd number leaves a remainder of 1.

Modular Arithmetic

Modular arithmetic is a system where we work with remainders after division. We say that two integers a and b are congruent modulo m if they have the same remainder when divided by m. This is denoted by:

$a\equiv b(\mathrm{mod}m)⟺m|(a-b)$

Example:

• $7\equiv 1(\mathrm{mod}3)$ because both 7 and 1 have a remainder of 1 when divided by 3.

Diophantine Equations

Diophantine equations are polynomial equations where we are interested in finding integer solutions.

Famous Examples:

• Fermat’s Last Theorem: A famous example is Fermat’s Last Theorem, which states that there are no positive integer solutions to the equation $x^n+y^n=z^n$ for any integer value of n greater than 2. This theorem was famously proposed by Pierre de Fermat and remained unproven for centuries until finally proved by Andrew Wiles in 1994.

• Catalan’s Conjecture: Another famous example is Catalan’s Conjecture, which states that the only solution in positive integers to the equation $y^a-x^b=1$ is $3^2-2^3=1$. This conjecture was proven by Preda Mihăilescu in 2002.

Analyzing the Equation $x^a+x^b=y^c+y^d+1$

The equation $x^a+x^b=y^c+y^d+1$ appears to be a general form of an equation involving exponents. However, we can quickly deduce that this equation has no integer solutions. Here’s why:

Parity and Even/Odd Numbers:

An integer’s parity refers to whether it is even or odd. Even numbers are multiples of 2, while odd numbers leave a remainder of 1 when divided by 2.

The parity of a number is preserved under multiplication. If we multiply two even numbers, the result is even. If we multiply two odd numbers, the result is odd. If we multiply an even number by an odd number, the result is even.

Analyzing the Equation:

1. Left-Hand Side (LHS): The left-hand side of the equation, $x^a+x^b$, is always even for any integer x and any positive integers a and b. This is because:

   • If x is even, then any power of x is also even.
   • If x is odd, then any power of x is also odd. Since the sum of two odd numbers is always even, $x^a+x^b$ will be even.

2. Right-Hand Side (RHS): The right-hand side of the equation, $y^c+y^d+1$, is always odd for any integer y and any positive integers c and d. This is because:

   • If y is even, then any power of y is also even.
   • If y is odd, then any power of y is also odd. The sum of two even numbers is always even, but adding 1 makes the result odd.

3. Contradiction: Since the left-hand side (LHS) is always even and the right-hand side (RHS) is always odd, they cannot be equal for any integer values of x, y, a, b, c, and d. This contradiction proves that the equation has no integer solutions.

By analyzing the parity of the terms involved, we can quickly determine that this equation has no integer solutions. This demonstrates how basic properties of even and odd numbers can be used to analyze the solvability of equations involving integers.

Analyzing the Equation $x^3-x-1=y^2$

The equation $x^3-x-1=y^2$ presents an interesting problem. Can an expression of this form (the left-hand side, LHS) ever be equal to a perfect square (the right-hand side, RHS) for integer values of x and y?

We can use modular arithmetic to explore this question. Instead of focusing on even/odd (mod 2), let’s examine the remainders when divided by 3 (mod 3).

Mod 3 Analysis:

1. LHS ($x^3-x-1$): Let’s check the possible values of the LHS for $x=0,1,2$ (representing all possible remainders modulo 3):

   • x = 0: $0^3-0-1=-1\equiv 2(\mathrm{mod}3)$.
   • x = 1: $1^3-1-1=-1\equiv 2(\mathrm{mod}3)$.
   • x = 2: $2^3-2-1=5\equiv 2(\mathrm{mod}3)$.

   Notice that for any integer x, the LHS always has a remainder of 2 when divided by 3.

2. RHS ($y^2$): Similarly, let’s check the possible values of the RHS for $y=0,1,2$:

   • y = 0: $0^2=0\equiv 0(\mathrm{mod}3)$.
   • y = 1: $1^2=1\equiv 1(\mathrm{mod}3)$.
   • y = 2: $2^2=4\equiv 1(\mathrm{mod}3)$.

   Notice that for any integer y, the RHS always has a remainder of 0 or 1 when divided by 3.

3. Contradiction: Since the LHS is always congruent to 2 (mod 3) and the RHS is always congruent to 0 or 1 (mod 3), there cannot be any integer values of x and y for which the equation $x^3-x-1=y^2$ holds.

Key Takeaway: Modular arithmetic provides a powerful tool for analyzing equations involving integers, helping us to uncover constraints and impossibilities. By examining the remainders of expressions modulo a chosen modulus, we can sometimes quickly determine if a solution is feasible or not.

Continue here: 13 Modular Arithmetics, Set of Residues, Diffie-Hellman, Multiplicative Inverse, Chinese Remainder Theorem