07 Linear Transformations, Linear Systems of Equations, PageRank

Lecture from 09.10.2024 | Video: Videos ETHZ

Linear Transformations

We showed last time that a transformation is linear if it is additive and homogenous.

1. $T(x+y)=T(x)+T(y)$
2. $T(\lambda x)=\lambda T(x)$

Lemma 2.28:

Let $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a linear transformation. $x_1,\dots x_l\in {\mathbb{R}}^n$, ${\lambda }_1,\dots ,{\lambda }_l\in \mathbb{R}$ then:

$$T\left(\sum _{j=1}^{\ell }{\lambda }_j{\mathbf{x}}_j\right)=\sum _{j=1}^{\ell }{\lambda }_{j}T({\mathbf{x}}_j)$$

To be rigorous let us prove this properly by using induction. We are going to use this method in order to not use the “unrigorous” dotted notation which uses $\dots$ in it’s proof.

The matrix of a linear transformation (Theorem 2.29)

Let $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a linear transformation. Then there exists an unique $m\times n$ matrix $A$ such that $T=T_A$.

Now this might seem daunting at first, but once we prove it it makes the job of working with generic linear transformations much easier, since we only have to think of matrices.

Proof:

In order for $T=T_A$ we need:

$T(e_j)=T_A(e_j)=A{e}_j:\forall j=1\dots n$ which means that the linear transformation of the unit vector $e_j$ is the same for both transformations.

This way the only matrix $A$ we can get is:

$$A=\left[\begin{array}{cccc}|& |& & |\\ T({\mathbf{e}}_1)& T({\mathbf{e}}_2)& \cdots & T({\mathbf{e}}_n)\\ |& |& & |\end{array}\right]$$

This works, because for all $x\in {\mathbb{R}}^n$:

$$\begin{array}{rl}{T}_A(\mathbf{x})& \begin{array}{cc}=& A\mathbf{x}\end{array}\\ & =\sum _{j=1}^n{x}_{j}T({\mathbf{e}}_j)\\ & =T\left(\sum _{j=1}^n{x}_j{\mathbf{e}}_j\right)\\ & =T(x)\end{array}$$

Now using this information we can show some general properties of linear transformations:

Systems of Linear Equations

A system of linear equations is a collection of two or more linear equations involving the same variables. The goal is to find values for these variables that simultaneously satisfy all the equations in the system.

A system of linear equations in $m$ equations and n variables $x_1,x_2,\dots ,x_n$ is of the form:

$$\begin{array}{rcl}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n& =& b_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n& =& b_2\\ & ⋮& \\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n& =& b_m\end{array}$$

Or in a “more simpler” standardized matrix-vector form:

$$A\mathbf{x}=\mathbf{b}:\underset{A,m\times n}{\underbrace{\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]}}\underset{\mathbf{x}\in {\mathbb{R}}^n}{\underbrace{\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]}}=\underset{\mathbf{b}\in {\mathbb{R}}^m}{\underbrace{\left[\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_m\end{array}\right]}}$$

Let us call A: “coefficient matrix”, b = “right side” and x: “vector of the variables”. A and b are known real values. The x vector is the “unknown”.

The following observation (Beobachtung 3.2) becomes trivial:

Let $A$ be a a $m\times n$ matrix. The columns of A are linearly independent if and only if the system $Ax=0$ has a single unique trivial solution ($x=0$).

Pagerank Algorithm (Google)

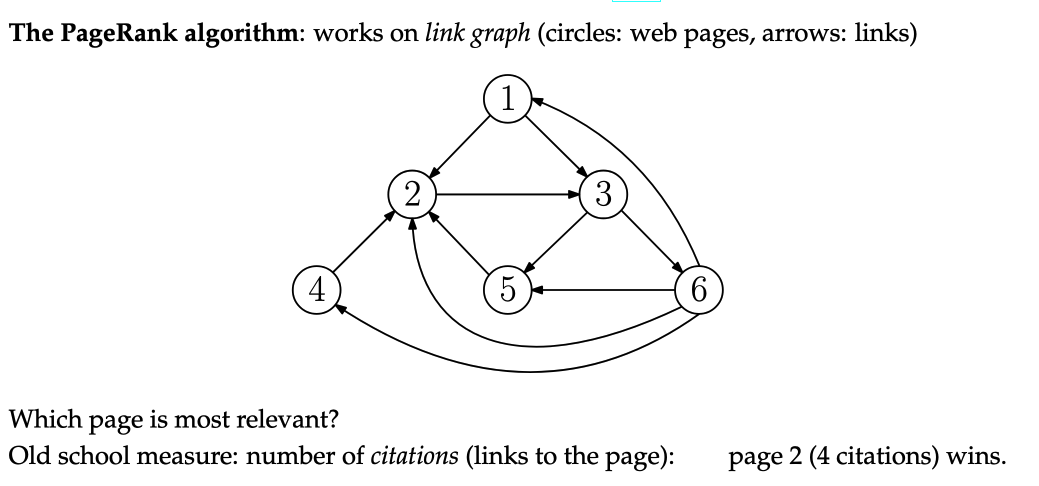
PageRank-Principles:

• Citations from relevant pages are worth more (no spamming links from useless sites)
• Citations from sites which cite a lot of sites are worth less

Now you might see that we have a small problem. We want to define the rank of a page based on the rank of other pages (which is also based on the rank of other pages…), effectively creating a recursive problem.

Relevance: Sum of the relevance of the sites citing this site, divided by the number of sites which are sited on that site.

$$x_2=\frac{x_1}{2}+x_4+x_5+\frac{x_6}{4}$$

Analogously for the other sites…

And wow, look at this, we got a system of 6 linear equations and 6 variables (sites). Unfortunately we have a useless solution of $0$.

Fix:

We will use a slight approximation using a damping factor $d$ close to $1$ (for example, $d=7/8$):

$$x_2=(1-d)+d\left(\frac{x_1}{2}+x_4+x_5+\frac{x_6}{4}\right)$$

This now allows us to have a unique (non-trivial) solution to our problem ($d=7/8$):

$$x_1=0.31797,x_2=1.6761,x_3=1.7307,x_4=0.31797,x_5=1.0751,x_6=0.88217$$

Page 3 (rank 1.7307) wins.

Continue here: 08 Gauss Elimination, Elimination Matrices and Solution Sets