08 Relations, Compositions and Properties

Lecture from: 14.10.2024 | Video: Videos ETHZ

Relations

In essence, a relation is simply a connection or association between elements from two sets. Imagine you have a set of students ($A$) and a set of courses they enroll in ($B$). A relation could describe which students take which courses. This connection can be represented as pairs: each pair links a student to the course(s) they are enrolled in.

Formally, we define a relation $\rho$ as: $\rho \subseteq A\times B$ $(a,b)\in \rho \equiv a\rho b$

This means that $\rho$ is a subset of the Cartesian product of sets $A$ and $B$. The Cartesian product ($A\times B$) is the set of all possible ordered pairs where the first element comes from $A$ and the second element comes from $B$.

Example: ≤

• $A=B=\mathbb{N}$
• $\rho =\le$
• $2\le 5$
• $(2,5)\in \le$

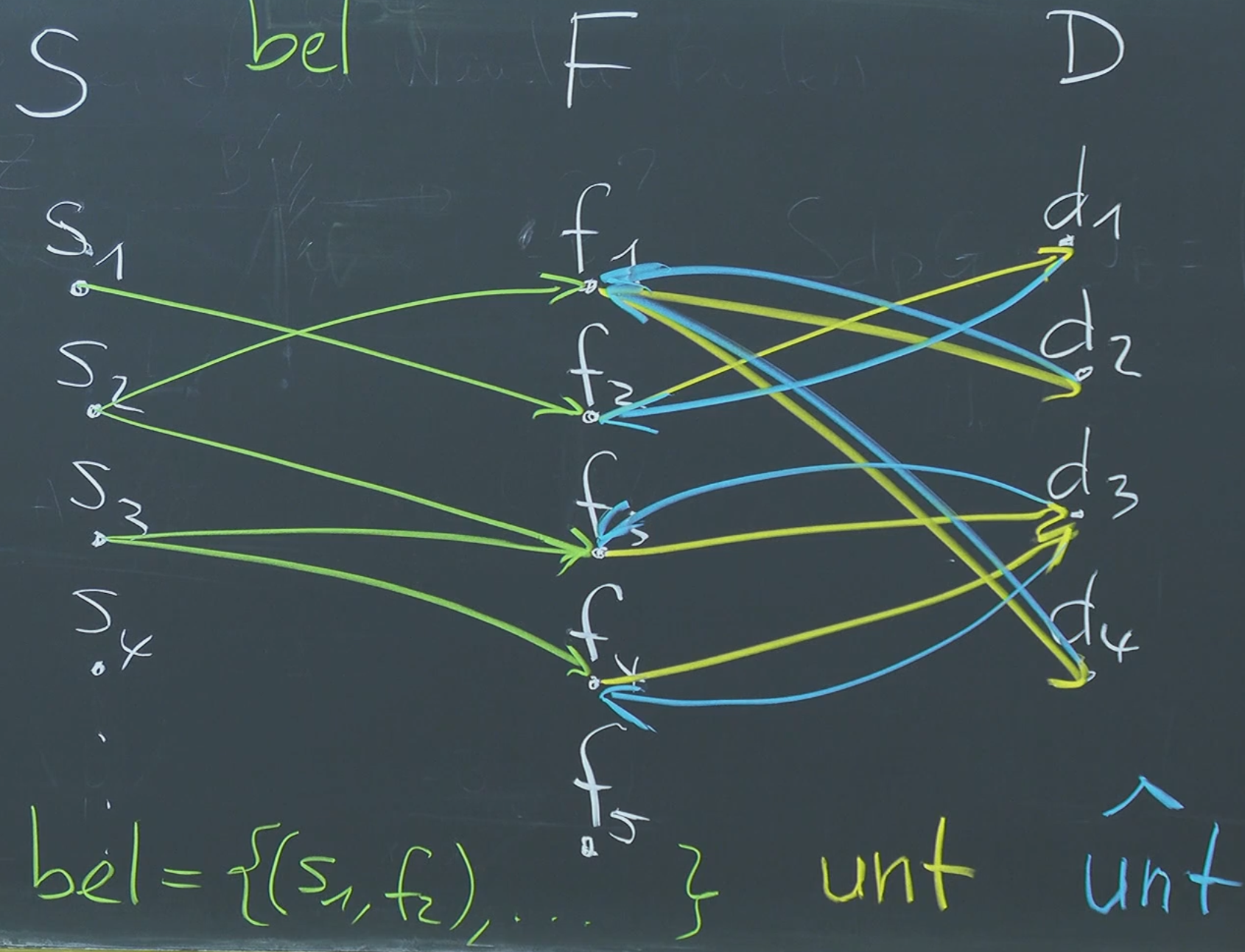
Example: School

Let’s say:

• $A=\{\text{Alice, Bob, Carol}\}$ (Set of students)
• $B=\{\text{Math, Physics, History}\}$ (Set of courses)

A relation $\rho$ could represent the following:

• $\rho =\{(\text{Alice, Math}),(\text{Bob, Physics}),(\text{Carol, History})\}$

We now introduce a new set:

• $T=\{\text{David, Emily, Frank}\}$ (Set of teachers)

And a relation $\tau$ that connects subjects with their respective teachers:

• $\tau =\{(\text{Math, David}),(\text{Physics, Emily}),(\text{History, Frank})\}$

Visualizing the Connections:

• Students (A): Alice, Bob, Carol
• Courses (B): Math, Physics, History
• Teachers (T): David, Emily, Frank

And the relations:

• $\rho$ connects students to courses they take (e.g., Alice takes Math).
• $\tau$ connects subjects with teachers who teach them (e.g., David teaches Math).

Inverse

Given a relation $\rho \subseteq A\times B$, its inverse, denoted as $\hat{\rho }$, is defined as:

$$\hat{\rho }=\{(b,a)\mid (a,b)\in \rho \}$$ $$b\hat{\rho }a⟺a\rho b$$

Example: Inverse of ≤

$$\hat{\le }=\ge$$

Example: Inverse of School Example

• $\hat{\rho }=\{(\text{Math, Alice}),(\text{Physics, Bob}),(\text{History, Carol})\}$ — “Subject is taken by Student”
• $\hat{\tau }=\{(\text{David, Math}),(\text{Emily, Physics}),(\text{Frank, History})\}$ — “Teacher teaches Subject”

Example: Parent Relationship

Let us define $\text{isparentof (ip)}$ as $x\text{ ip }y⟺x\text{ is parent of }y$. Then the inverse is: $\widehat{\text{ip}}=\text{ischildof (ic)}$.

Composition of Relations

The composition of two relations, $\rho$ and $\sigma$, is denoted as $\rho \circ \sigma$. It represents a new relation formed by applying $\rho$ and then $\sigma$.

Formal Definition:

If $\rho \subseteq A\times B$ and $\sigma \subseteq B\times C$, then their composition, $\rho \circ \sigma$, is defined as:

$$\rho \circ \sigma =\{(a,c)\mid \exists b\in B:(a,b)\in \rho \text{ and }(b,c)\in \sigma \}$$

Example: Student-Subject-Teacher

• $\rho =\{(\text{Alice},\text{Math}),(\text{Bob},\text{Physics})\}$ (Student takes Subject)
• $\sigma =\{(\text{Math},\text{David}),(\text{Physics},\text{Emily})\}$ (Subject is taught by Teacher)

Then $\rho \circ \sigma =\{(\text{Alice},\text{David}),(\text{Bob},\text{Emily})\}$ (Student is taught by Teacher).

Example: Child-Parent

• $\text{ip}\circ \text{ip}=\text{igp}$ (is grandparent of)
• $(\text{ic}\circ \text{ip})\setminus \text{id}=\text{ihs}$ (is half-sibling of) — The identity relation (id) is removed to exclude a person being their own half-sibling.

Proof of Lemma 3.8

Lemma 3.8: $\widehat{\rho \circ \sigma }=\hat{\sigma }\circ \hat{\rho }$

Proof:

• $a\widehat{\rho \circ \sigma }c⟺c(\rho \circ \sigma )a$
• $⟺\exists b(c\rho b\wedge b\sigma a)$
• $⟺\exists b(b\hat{\rho }c\wedge a\hat{\sigma }b)$
• $⟺a(\hat{\sigma }\circ \hat{\rho })c$

Visualization using Matrices

Relations can be represented visually using matrices, offering a structured way to understand their connections.

Matrix Representation:

Consider a relation $R$ on a set $A=\{a_1,a_2,a_3\}$. We can represent this relation as a matrix $M_R$ where:

• The rows and columns of the matrix correspond to the elements in set $A$.
• An entry $M_{ij}$ is 1 if $(a_i,a_j)\in R$ (meaning there’s a connection from $a_i$ to $a_j$) and 0 otherwise.

Example:

Let’s say $R=\{(a_1,a_2),(a_2,a_3)\}$. The matrix representation of $R$ would be:

$$M_R=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right)$$

Inverse Relation and Matrix Transposition:

The inverse relation $R^{-1}$ of a relation $R$ is defined as: $(a,b)\in R^{-1}$ if and only if $(b,a)\in R$.

Importantly, the matrix representation of the inverse relation is simply the transpose of the original matrix.

Example (continued):

The inverse relation $R^{-1}$ would be: $(a_2,a_1),(a_3,a_2)$. The transposed matrix $M_{R^{-1}}$ is:

$$M_{R^{-1}}=\left(\begin{array}{ccc}0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)$$

Properties and Rules

1. Associativity:

Composition of relations is associative. If we have three relations $\rho$, $\sigma$, and $\tau$ (where $\rho$ ⊆ $A\times B$, $\sigma$ ⊆ $B\times C$, and $\tau$ ⊆ $C\times D$), then: ($\rho$ ∘ $\sigma$) ∘ $\tau$ = $\rho$ ∘ ($\sigma$ ∘ $\tau$)

2. Non-Commutativity:

Composition of relations is not commutative. This means that generally, $\rho$ ∘ $\sigma$ ≠ $\sigma$ ∘ $\rho$.

3. Identity Relation:

There exists an identity relation for each set, denoted as $I_A$ if A is our set.

• $I_A$ = {($a$, $a$) | $a$ ∈ $A$} – It connects an element only to itself. Applying the identity relation doesn’t change anything.

Example with Composition: Let $\rho$ be a relation “student takes a subject” and $I_B$ be the identity relation on the set of subjects. Then: $\rho$ ∘ $I_B$ = $\rho$

This means taking a subject followed by being that same subject doesn’t change anything!

4. Reflexivity, Symmetry, Antisymmetry, Transitivity, Asymmetry:

These are properties that relations can possess. A relation is:

Reflexive

If for every element ‘a’ in set A, ($a$, $a$) $\in$ $\rho$ Alternate: $id\subseteq \rho$

Similarly irreflexive is the opposite: $a\cancel{\rho }a$ for every ‘a’ in A.

Symmetric

If for every pair ($a$, $b$) $\in$ $\rho$, then ($b$, $a$) $\in$ $\rho$ Alternate: $\rho =\hat{\rho }$

Antisymmetric

If for every pair ($a$, $b$) and ($b$, $a$) $\in$ $\rho$, then $a=b$. (If (a, b) and (b, a) are both in the relation, then ‘a’ and ‘b’ must be the same element.) Same as: $a\rho b⟺b\rho a$ Alternative: A relation $\rho$ is antisymmetric if it is true for all $a,b\in A$ if $\rho \cap \hat{\rho }\subseteq id$

Transitive

If for every triple ($a$, $b$), ($b$, $c$) $\in$ $\rho$, then ($a$, $c$) $\in$ $\rho$. Same as: $a\rho b\wedge b\rho c⟹a\rho c$ Alternative: A relation $\rho$ is transitive if and only if ${\rho }^2\subseteq \rho$.

Asymmetric

If for every pair ($a$, $b$) $\in$ $\rho$, then ($b$, $a$) $\notin$ $\rho$. (In other words, if (a, b) is in the relation, then (b, a) cannot be.)

Transitive Closure

The transitive closure of a relation $R$ on a set $A$ is the smallest transitive relation containing $R$. In simpler terms, it includes all pairs $(x,y)$ where there exists a path from $x$ to $y$ through $R$, even if that path involves multiple steps.

Formalization:

Let $R$ be a relation on set $A$. The transitive closure of $R$, denoted as $R^{\ast }$, can be defined recursively as follows:

• $R\subseteq R^{\ast }$ (The original relation is included)
• If $(x,y)\in R^{\ast }$ and $(y,z)\in R$, then $(x,z)\in R^{\ast }$

Example: “Parent” and “Ancestor” Relationships”

Let’s say our set $A$ represents people, and the relation $R$ is defined as “is a parent of.” For instance: (John, Mary) $\in R$ (John is Mary’s parent)

Now, we want to find the transitive closure $R^{\ast }$ which would represent the “ancestor” relationship.

• Direct Parents: The initial relation includes direct parent-child pairs like (John, Mary).
• Transitive Steps: Since John is Mary’s parent, and Mary could potentially have children who are also descendants of John, we include those relationships in $R^{+}$ too.

For example:

• If Mary has a child named David, then (John, David) would be in $R^{\ast }$ because John is the ancestor of David through his direct relationship with Mary.

The transitive closure can grow quite large for complex relations with many elements. There are algorithms to efficiently compute the transitive closure, but it’s essential to understand its concept and how it extends a relation beyond direct connections.

Continue here: 09 Equivalency Relation and Classes, Partitions, Partially Ordered Sets