18 Orthonormal Bases, Properties of Orthogonal Matrices

Lecture from 15.11.2024 | Video: Videos ETHZ

Orthonormal Bases

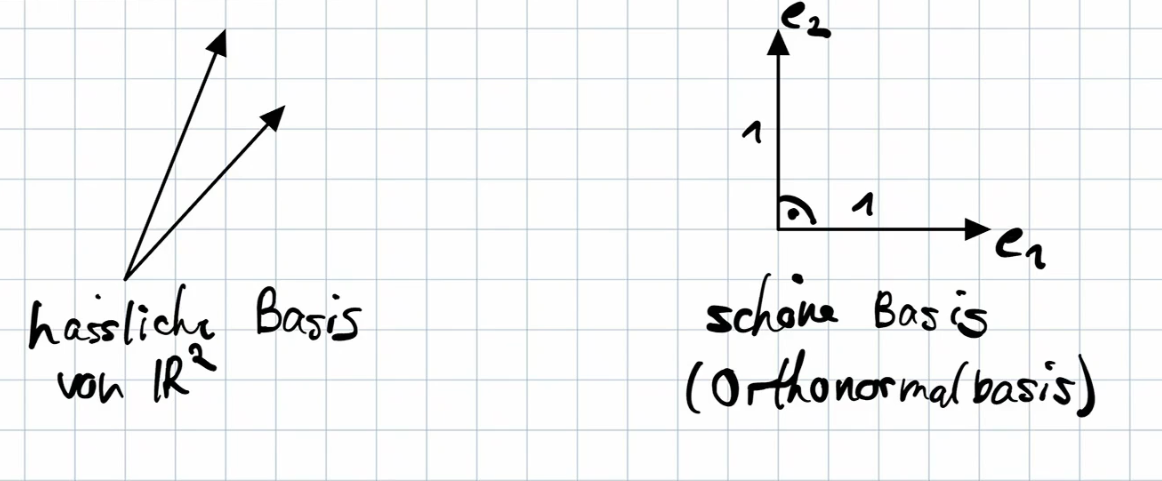
Orthonormal Vectors (Definition 5.4.1)

Vectors ${\mathbf{q}}_1,{\mathbf{q}}_2,\dots ,{\mathbf{q}}_n\in {\mathbb{R}}^m$ are orthonormal if they are pairwise orthogonal and have unit length (norm 1). Mathematically:

${\mathbf{q}}_i^T{\mathbf{q}}_j={\delta }_{ij}=\{\begin{array}{ll}0,& \text{if }i\ne j\\ 1,& \text{if }i=j\end{array}$

where ${\delta }_{ij}$ is the Kronecker delta.

• Matrix Form: If $Q$ is a matrix whose columns are the ${\mathbf{q}}_i$ vectors, then the vectors are orthonormal if and only if $Q^{T}Q=I$ (where $I$ is the identity matrix. Note that ${\mathbf{q}}_i^T{\mathbf{q}}_j$ is the entry in the $i$-th row and $j$-th column of $Q^{T}Q$).
• Non-Square Matrices: $Q$ need not be square. If it is not square, $Q{Q}^T=I$ does not necessarily hold (though $Q^{T}Q=I$ does).
• Example: The standard basis vectors in ${\mathbb{R}}^m$ are orthonormal.

Orthogonal Matrices (Definition 5.4.3)

A square matrix $Q\in {\mathbb{R}}^{n\times n}$ is orthogonal if $Q^{T}Q=I$. This implies:

• $Q^T=Q^{-1}$
• $Q{Q}^T=I$
• The columns of $Q$ form an orthonormal basis for ${\mathbb{R}}^n$.

2x2 Rotation Matrix (Example 5.4.4)

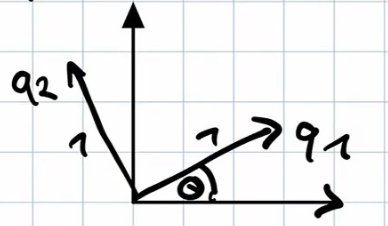
The 2x2 rotation matrix $R_{\theta }$: $R_{\theta }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$ rotates a vector counter-clockwise by angle $\theta$ and is an orthogonal matrix (verify $R_{\theta }^T{R}_{\theta }=I$).

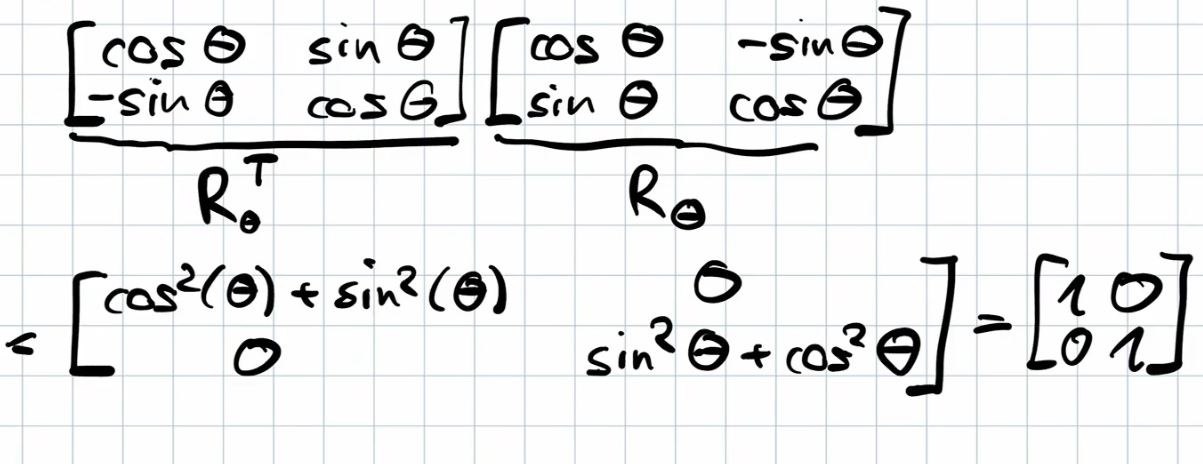
Permutation Matrices (Example 5.4.5)

A permutation matrix is a square matrix where each row and column contains exactly one entry of 1 and all other entries are 0. They represent permutations of vector components. Permutation matrices are orthogonal.

• Construction: The permutation matrix A corresponding to a permutation and bijective transformation $\pi :[n]\to [n]$ has entries $A_{ij}=1$ if $\pi (i)=j$ and $0$ otherwise.

  

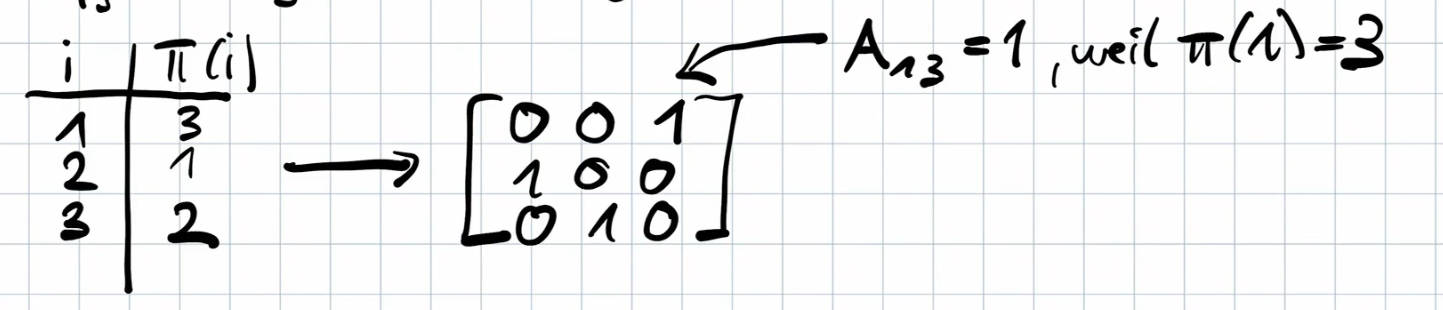
• Property: For every permutation matrix A, there exists a positive integer $k$ such that $A^k=I$.

Properties of Orthogonal Matrices (Proposition 5.4.6)

Orthogonal matrices preserve norms and inner products (scalar products). That is, for all $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^n$:

(i) $\Vert Q\mathbf{x}\Vert =\Vert \mathbf{x}\Vert$ (ii) $(Q\mathbf{x}{)}^T(Q\mathbf{y})={\mathbf{x}}^T\mathbf{y}$

Proof:

• (ii) $(Q\mathbf{x}{)}^T(Q\mathbf{y})={\mathbf{x}}^T{Q}^{T}Q\mathbf{y}={\mathbf{x}}^{T}I\mathbf{y}={\mathbf{x}}^T\mathbf{y}$
• (i) $\Vert Q\mathbf{x}{\Vert }^2=(Q\mathbf{x}{)}^T(Q\mathbf{x})={\mathbf{x}}^T\mathbf{x}=\Vert \mathbf{x}{\Vert }^2$. Taking the square root of both sides gives $\Vert Q\mathbf{x}\Vert =\Vert \mathbf{x}\Vert$.

Projections with Orthonormal Bases (Proposition 5.4.7)

Let $S$ be a subspace of ${\mathbb{R}}^m$, and let ${\mathbf{q}}_1,{\mathbf{q}}_2,\dots ,{\mathbf{q}}_n$ be an orthonormal basis for $S$. Let $Q=[{\mathbf{q}}_1,{\mathbf{q}}_2,\dots ,{\mathbf{q}}_n]$.

(i) For all $\mathbf{b}\in {\mathbb{R}}^m$, the projection of $\mathbf{b}$ onto $S$ is given by ${\text{proj}}_S(\mathbf{b})=P\mathbf{b}$, where $P=Q{Q}^T$. (ii) The least squares solution of $Q\mathbf{x}=\mathbf{b}$ is $\hat{\mathbf{x}}=Q^T\mathbf{b}$.

Proof:

• (i) By Theorem 5.2.6, $P=Q(Q^{T}Q{)}^{-1}{Q}^T$. Since $Q$ has orthonormal columns, $Q^{T}Q=I$, so $P=Q{Q}^T$.
• (ii) The least squares solution is given by $\hat{\mathbf{x}}=(Q^{T}Q{)}^{-1}{Q}^T\mathbf{b}$. Since $Q^{T}Q=I$, we have $\hat{\mathbf{x}}=Q^T\mathbf{b}$.

Orthogonal Matrices and Rotations

Orthogonal matrices, especially those with determinant 1 (known as special orthogonal matrices), represent rotations in ${\mathbb{R}}^n$. While general orthogonal matrices can also encompass reflections, rotations are their fundamental transformation.

Key Properties of Orthogonal Matrices:

• Inverse equals Transpose: A defining characteristic of an orthogonal matrix $Q$ is that its inverse equals its transpose: $Q^{-1}=Q^T$. This is crucial for understanding their connection to rotations. (See proof in previous responses.)

• Transpose/Inverse of a Product: For any matrices A and B (of compatible dimensions), $(AB{)}^T=B^T{A}^T$ and $(AB{)}^{-1}=B^{-1}{A}^{-1}$.

• Product of Orthogonal Matrices: If A and B are orthogonal, then (AB) is also orthogonal: $(AB{)}^{-1}=B^{-1}{A}^{-1}=B^T{A}^T=(AB{)}^T$.

Why Orthogonal Matrices Represent Rotations:

1. Preservation of Length (Norm): Orthogonal matrices preserve vector lengths. If $\mathbf{x}$ is a vector and $Q$ is orthogonal, $\Vert Q\mathbf{x}\Vert =\Vert \mathbf{x}\Vert$. This is a defining feature of rotations. (See proof above.)

2. Preservation of Inner Products (and Angles): Orthogonal matrices preserve inner products. If $Q$ is orthogonal, $(Q\mathbf{x}{)}^T(Q\mathbf{y})={\mathbf{x}}^T{Q}^{T}Q\mathbf{y}={\mathbf{x}}^T\mathbf{y}$. Since angles between vectors are determined by their inner products and norms (both preserved by $Q$), orthogonal matrices preserve angles.

3. Orthonormal Basis Transformation: The columns (and rows) of an orthogonal matrix constitute an orthonormal basis. When $Q$ acts on the standard basis vectors, it rotates them to a new orthonormal basis, effectively rotating the entire coordinate system. Proof: Let ${\mathbf{e}}_i$ be a standard basis vector. $Q{\mathbf{e}}_i$ is the $i$-th column of $Q$, which is a vector in the new orthonormal basis.

4. Determinant: The determinant of an orthogonal matrix $Q$ is either 1 or -1. Proof: Since $Q^{T}Q=I$, taking the determinant of both sides gives $\det (Q^T)\det (Q)=\det (I)=1$. Because $\det (Q^T)=\det (Q)$, we have $(\det (Q){)}^2=1$, so $\det (Q)=\pm 1$. A determinant of 1 indicates a pure rotation, while -1 signifies a rotation combined with a reflection. Note: We didn’t look at this in the lecture…

Example in ${\mathbb{R}}^2$:

The standard rotation matrix $R_{\theta }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$ rotates vectors counterclockwise by $\theta$. It’s straightforward to confirm $R_{\theta }^T{R}_{\theta }=I$ and $\det (R_{\theta })=1$, proving it’s a rotation.

Additional Properties

When $Q$ is square ($m=n$), $Q{Q}^T=I$, and $\mathbf{x}=Q^T\mathbf{b}$ can be written as:

$\mathbf{x}=Q^T\mathbf{b}=\left[\begin{array}{c}{\mathbf{q}}_1^T\\ ⋮\\ {\mathbf{q}}_n^T\end{array}\right]\mathbf{b}=\left[\begin{array}{c}{\mathbf{q}}_1^T\mathbf{b}\\ ⋮\\ {\mathbf{q}}_n^T\mathbf{b}\end{array}\right]$

This shows $\mathbf{x}$ is a linear combination of the basis vectors ${\mathbf{q}}_i$ where the coefficient of ${\mathbf{q}}_i$ is ${\mathbf{q}}_i^T\mathbf{b}$: $\mathbf{x}=Q(Q^T\mathbf{x})={\sum }_{i=1}^m({\mathbf{q}}_i^T\mathbf{x}){\mathbf{q}}_i$

In the special case where ${\mathbf{q}}_i={\mathbf{e}}_i$ (the standard basis vectors), we recover $\mathbf{x}={\sum }_{i=1}^m{x}_i{\mathbf{e}}_i$.