12 Vector Spaces, Subspaces

Lecture from 25.10.2024 | Video: Videos ETHZ

Vector Spaces

What exactly is a vector? A common initial thought might be an element of ${\mathbb{R}}^m$. While true, this is merely an example of a vector, not a definition. We need a more precise and encompassing understanding.

Definition of a Vector Space (Definition 4.1)

A vector is an element of a vector space. Vector spaces are characterized by two key operations on their elements: vector addition and scalar multiplication. These operations must adhere to specific rules to ensure the space behaves in a consistent and predictable manner.

Formal Definition: A vector space is a triple $(V,+,\cdot )$ where:

• $V$: A set containing the vectors.
• $+$: A function $+:V\times V\to V$ representing vector addition. It takes two vectors from $V$ and returns another vector in $V$.
• $\cdot$: A function $\cdot :\mathbb{R}\times V\to V$ representing scalar multiplication. It takes a real number (scalar) and a vector from $V$ and returns another vector in $V$.

These operations must satisfy the following eight axioms for all $u,v,w\in V$ and all $\lambda ,\mu \in \mathbb{R}$:

1. Commutativity of addition: $v+w=w+v$
2. Associativity of addition: $u+(v+w)=(u+v)+w$
3. Existence of a zero vector: There exists a vector $0\in V$ such that $v+0=v$ for all $v\in V$.
4. Existence of additive inverses: For every $v\in V$, there exists a vector $-v\in V$ such that $v+(-v)=0$.
5. Scalar multiplication identity: $1\cdot v=v$
6. Compatibility of scalar multiplication: $(\lambda \cdot \mu )v=\lambda \cdot (\mu \cdot v)$
7. Distributivity of scalar multiplication over vector addition: $\lambda \cdot (v+w)=\lambda v+\lambda w$
8. Distributivity of scalar multiplication over scalar addition: $(\lambda +\mu )v=\lambda v+\mu v$

Examples of Vector Spaces

We’ll now explore concrete examples of vector spaces, clarifying how the abstract definition applies in specific cases.

The Real Coordinate Space: ${\mathbb{R}}^m$ (Observation 4.2)

The set ${\mathbb{R}}^m$ consists of all $m$-tuples of real numbers. We represent elements (vectors) in ${\mathbb{R}}^m$ as ordered lists:

$v=(v_1,v_2,...,v_m)$, where $v_i\in \mathbb{R}$.

Vector addition and scalar multiplication are defined component-wise:

• Addition (Definition 1.1): If $v=(v_1,...,v_m)$ and $w=(w_1,...,w_m)$, then $v+w=(v_1+w_1,...,v_m+w_m)$. For example, in ${\mathbb{R}}^2$, $(1,2)+(3,4)=(4,6)$.
• Scalar Multiplication (Definition 1.3): If $v=(v_1,...,v_m)$ and $\lambda \in \mathbb{R}$, then $\lambda v=(\lambda v_1,...,\lambda v_m)$. For example, in ${\mathbb{R}}^3$, $2\cdot (1,0,-1)=(2,0,-2)$.

$({\mathbb{R}}^m,+,\cdot )$ forms a vector space because these operations satisfy all eight axioms of a vector space. ${\mathbb{R}}^m$ is often the first and most familiar example encountered when learning about vector spaces.

The Space of Polynomials: $\mathbb{R}[x]$ (Lemma 4.4 and Definition 4.3)

The set $\mathbb{R}[x]$ contains all polynomials with real coefficients. A polynomial $p$ is expressed as:

$p(x)={\sum }_{i=0}^n{a}_i{x}^i=a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n$, where $a_i\in \mathbb{R}$. The largest $i$ such that $a_i\ne 0$ is the degree of the polynomial. The zero polynomial (all $a_i=0$) has a degree of -1 by convention (Definition 4.3).

Polynomial addition and scalar multiplication are defined as:

• Addition: $(p+q)(x)={\sum }_{i=0}^{\max (n,m)}(a_i+b_i)x^i$ where $p(x)$ has degree $n$ and $q(x)$ has degree $m$. Example: $(2x+1)+(x^2-3)=x^2+2x-2$.

• Scalar Multiplication: $(\lambda p)(x)={\sum }_{i=0}^n(\lambda a_i)x^i$. Example: $2\cdot (x^2+1)=2x^2+2$.

$(\mathbb{R}[x],+,\cdot )$ constitutes a vector space (Lemma 4.4), satisfying all eight axioms. This example demonstrates that vector spaces can encompass more abstract objects than just tuples of numbers or matrices. The fact that polynomials form a vector space is a consequence of the way addition and scalar multiplication are defined for polynomials, which align with the axioms of a vector space.

This approach integrates the definition of a polynomial (Definition 4.3) directly into the explanation of why the set of all polynomials forms a vector space (Lemma 4.4). This makes the connection between the two concepts clearer and avoids redundancy.

The Space of Real Matrices: ${\mathbb{R}}^{m\times n}$ (Lemma 4.5)

The set ${\mathbb{R}}^{m\times n}$ comprises all $m\times n$ matrices with real entries. Matrices are rectangular arrays of numbers:

$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]$, where $a_{ij}\in \mathbb{R}$.

Standard matrix addition and scalar multiplication are defined as:

• Addition (Definition 2.2): If $A$ and $B$ are two $m\times n$ matrices, then $(A+B{)}_{ij}=a_{ij}+b_{ij}$. For example, $\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]+\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}1& 1\\ 4& 4\end{array}\right]$.

• Scalar Multiplication (Definition 2.2): If $A$ is an $m\times n$ matrix and $\lambda \in \mathbb{R}$, then $(\lambda A{)}_{ij}=\lambda a_{ij}$. For example, $3\cdot \left[\begin{array}{cc}1& 0\\ -1& 2\end{array}\right]=\left[\begin{array}{cc}3& 0\\ -3& 6\end{array}\right]$.

$({\mathbb{R}}^{m\times n},+,\cdot )$ forms a vector space, as these operations fulfill all the vector space axioms.

Uniqueness of the Zero Vector (Fact 4.6)

Within any vector space, the zero vector is unique. This can be proven directly from the axioms.

Proof: Assume that there are two distinct zero vectors, denoted as $0$ and $0^{\prime }$. We will show that they must be equal.

1. Using Axiom 3: Since $0$ is a zero vector, we have $v+0=v$ for any vector $v$ in the space.
2. Using Axiom 3 for $0^{\prime }$: Similarly, since $0^{\prime }$ is a zero vector, we have $v+0^{\prime }=v$ for any vector $v$ in the space.
3. Setting $v=0^{\prime }$ and $v=0$: Let’s apply these properties with $v=0^{\prime }$ and $v=0$:
   • $0^{\prime }+0=0^{\prime }$ (using Axiom 3 for $0$ and $v=0^{\prime }$)
   • $0+0^{\prime }=0$ (using Axiom 3 for $0^{\prime }$ and $v=0$)
4. Applying Commutativity (Axiom 1): The left-hand sides of these equations are equal by the commutativity of addition (Axiom 1): $0^{\prime }+0=0+0^{\prime }$.
5. Therefore: Combining the results, we get $0=0^{\prime }$.

Therefore, our initial assumption that $0$ and $0^{\prime }$ are distinct zero vectors is false. This proves that the zero vector in any vector space must be unique.

Abuse of Notation: $(V,+,\cdot )\to V$

In the context of vector spaces, we often use the notation $(V,+,\cdot )$ to represent the entire vector space, emphasizing that it is the set $V$ together with the specific operations of vector addition ($+$) and scalar multiplication ($\cdot$). This notation highlights the fundamental components that define a vector space.

However, for brevity and convenience, we often “abuse notation” and simply write $V$ to refer to the entire vector space, implicitly assuming that the associated operations ($+$ and $\cdot$) are understood. This convention is common in linear algebra and allows for more concise expression.

For instance, instead of saying “Let $(V,+,\cdot )$ be a vector space,” we might simply say “Let $V$ be a vector space.” It is understood from context that $V$ refers to a set equipped with specific addition and scalar multiplication operations.

While technically an abuse of notation, this simplification does not introduce ambiguity in most contexts and makes the presentation more compact.

Subspaces (Definition 4.8)

The concept of a subspace is crucial to understanding vector spaces. A subspace is a subset of a vector space that is itself a vector space under the same operations. This means that the subset must be closed under vector addition and scalar multiplication.

Formal Definition: Let $V$ be a vector space. A nonempty subset $U\subseteq V$ is a subspace of $V$ if the following two axioms hold for all $v,w\in U$ and all $\lambda \in \mathbb{R}$:

(i) Closure under addition: $v+w\in U$; (ii) Closure under scalar multiplication: $\lambda v\in U$.

Important Note: The zero vector $0$ always belongs to a subspace $U$. This follows directly from axiom (ii): for any $u\in U$, we have $0u=0\in U$.

Examples:

• The zero subspace: The set containing only the zero vector, {0}, is always a subspace of any vector space.
• Lines and Planes in ${\mathbb{R}}^3$: In three-dimensional space, lines and planes passing through the origin are subspaces. They are closed under vector addition and scalar multiplication, meaning that the sum of two vectors on the line/plane remains on the line/plane, and scaling a vector on the line/plane keeps it on the line/plane.

Visualizing Subspaces:

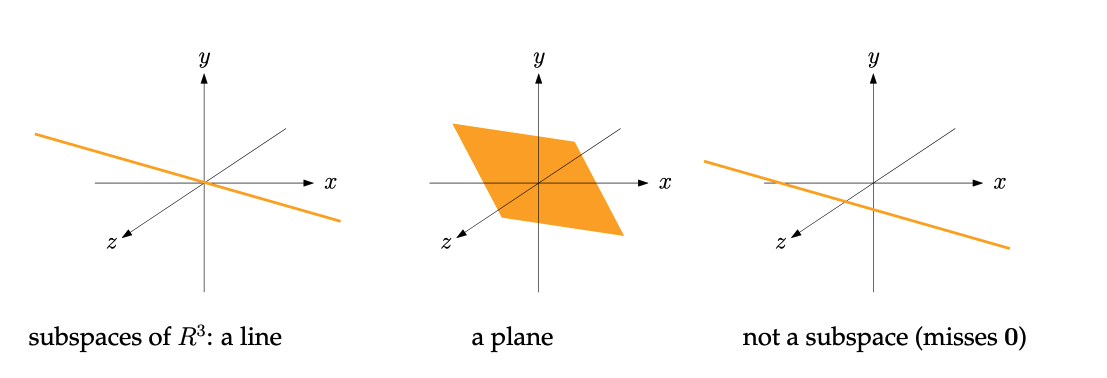
• Lines: Subspaces of ${\mathbb{R}}^3$ representing lines through the origin are the simplest example.
• Planes: Planes passing through the origin also form subspaces of ${\mathbb{R}}^3$.
• Not a Subspace: A line or plane not passing through the origin is not a subspace. It fails to contain the zero vector and, therefore, violates the closure properties.

Subspaces of ${\mathbb{R}}^m$ (Lemma 4.11)

Lemma 4.11: Let $A$ be an $m\times n$ matrix. Then $C(A)$ (the column space of $A$) is a subspace of ${\mathbb{R}}^m$.

Proof:

1. Closure under addition: Let $v,w\in C(A)$, which means there exist $x,y\in {\mathbb{R}}^n$ such that $v=Ax$ and $w=Ay$. Then, $v+w=Ax+Ay=A(x+y)$. Since $x+y\in {\mathbb{R}}^n$, we have $v+w\in C(A)$.
2. Closure under scalar multiplication: Let $v\in C(A)$ (so $v=Ax$ for some $x\in {\mathbb{R}}^n$) and let $\lambda \in \mathbb{R}$. Then, $\lambda v=\lambda Ax=A(\lambda x)$. Since $\lambda x\in {\mathbb{R}}^n$, we have $\lambda v\in C(A)$.

Therefore, $C(A)$ satisfies both axioms and is a subspace of ${\mathbb{R}}^m$.

Subspaces and Vector Spaces (Lemma 4.12)

Lemma 4.12: Let $V$ be a vector space and $U$ a subspace of $V$. Then $U$ is also a vector space (with the same “+” and “·” as $V$).

Proof: The proof follows directly from the definition of a subspace. Since $U$ is a subspace, it satisfies the closure axioms under addition and scalar multiplication, which are the same operations as in $V$. The remaining axioms (commutativity, associativity, etc.) also hold in $U$ because they hold in $V$, and $U$ is a subset of $V$.

Subspaces of…

Now, let’s examine some specific examples of subspaces within various familiar vector spaces.

… $\mathbb{R}[x]$: The Space of Polynomials

The polynomials without constant term:

The set of polynomials of the form $p(x)={\sum }_{i=1}^m{p}_i{x}^i$ (where $p_0=0$), forms a subspace of $\mathbb{R}[x]$. It is closed under addition and scalar multiplication:

• Adding two polynomials without constant terms results in another polynomial without a constant term.
• Multiplying a polynomial without a constant term by a scalar also yields a polynomial without a constant term.

The quadratic polynomials:

The set of quadratic polynomials of the form $p(x)=p_0+p_{1}x+p_2{x}^2$ forms a subspace of $\mathbb{R}[x]$. This is a special case of the polynomials of degree less than or equal to $n$, which also form a subspace.

Furthermore, this subspace is isomorphic to ${\mathbb{R}}^3$.

Isomorphism means that there exists a one-to-one and onto mapping (a bijection) between the two spaces that preserves the structure of the spaces. In other words, the two spaces “behave” the same way, even though their elements are represented differently.

For quadratic polynomials, the isomorphism is given by: $p(x)=p_0+p_{1}x+p_2{x}^2⟷(p_0,p_1,p_2)\in {\mathbb{R}}^3$

This mapping preserves addition and scalar multiplication:

• $(p+q)(x)⟷(p_0+q_0,p_1+q_1,p_2+q_2)$
• $(\lambda p)(x)⟷(\lambda p_0,\lambda p_1,\lambda p_2)$

Therefore, we can think of quadratic polynomials as being “equivalent” to vectors in ${\mathbb{R}}^3$. They have the same structure and behave in the same way under the operations of addition and scalar multiplication.

Generalization:

The set of polynomials of degree less than or equal to $n$ (where $n\ge 0$ is an integer) also forms a subspace of $\mathbb{R}[x]$. This can be generalized further: the set of polynomials with a degree less than or equal to any fixed integer $n$ always forms a subspace of $\mathbb{R}[x]$.

Using the same idea as for quadratic polynomials, $\mathbb{R}[x]$ of degree $n$ is isomorphic to ${\mathbb{R}}^n$.

… ${\mathbb{R}}^{2\times 2}$: The Space of $2\times 2$ Matrices

The symmetric matrices:

The set of $2\times 2$ matrices of the form $\left[\begin{array}{cc}a& b\\ b& d\end{array}\right]$ (where $a,b,d\in \mathbb{R}$) forms a subspace of ${\mathbb{R}}^{2\times 2}$. Adding two symmetric matrices results in another symmetric matrix, and scaling a symmetric matrix by a scalar also produces a symmetric matrix.

The matrices of trace 0:

The set of $2\times 2$ matrices of the form $\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$ (where $a+d=0$) forms a subspace of ${\mathbb{R}}^{2\times 2}$. The trace of a matrix is the sum of its diagonal elements.

… ${\mathbb{R}}^n$ (General Case)

It’s important to understand that many subspaces are not explicitly named or described in detail. For instance, in ${\mathbb{R}}^n$, you can have:

• Lines and Planes: As we saw earlier, these can be subspaces if they pass through the origin.
• The Span of a set of vectors: If you have a set of vectors in ${\mathbb{R}}^n$, their span (the set of all possible linear combinations of those vectors) is always a subspace.

These examples illustrate that subspaces are abundant and often represent interesting and meaningful subsets within vector spaces. The concept of subspaces is crucial for analyzing, understanding, and solving problems in linear algebra.

Continue here: 13 Vector Spaces, Bases, Dimension