08 Array Operations, Recursion

Lecture from: 15.10.2024 | Video: Videos ETHZ

Arrays

Operations on arrays, such as element replacement, validation checks, and merging, are commonly required in various programming tasks. Below, we will explore three common array operations: replacing values in an array, checking for conditions across all elements, and concatenating arrays.

Operations

Replace Method

Description:

The replace method modifies an array by replacing every occurrence of a specific value with a new value. This operation happens in place, meaning that the original array is modified directly, rather than creating a new array.

Method Signature:

void replace(int target, int[] array, int replacement)

target: The value to be replaced.
array: The array in which replacements are to be made.
replacement: The new value that will replace the target.

Example:

int[] data = {1, 4, 7, 4, 2};
replace(4, data, 0);
// The array 'data' is now modified to {1, 0, 7, 0, 2}.

Implementation:

void replace(int target, int[] array, int replacement) {
    for (int i = 0; i < array.length; i++) {
        if (array[i] == target) {
            array[i] = replacement;
        }
    }
}

All True Method

Description:

The allTrue method checks whether all elements of a boolean array are true. This method is commonly used in logical operations where we want to ensure that every condition has been satisfied.

Method Signature:

boolean allTrue(boolean[] values)

values: The boolean array to be checked.

Example:

boolean[] data = {true, false};
boolean result = allTrue(data); // returns false

Implementation (Version 1):

This version accumulates a conjunction of all elements in the array, which can be less efficient since the loop doesn’t stop once a false value is found.

boolean allTrue(boolean[] values) {
    boolean result = true;
    for (int i = 0; i < values.length; i++) {
        result = result && values[i];
    }
    return result;
}

Implementation (Version 2):

This version is more efficient because it short-circuits (terminates early) as soon as a false value is found. It uses an early return to reduce the number of iterations.

boolean allTrue(boolean[] values) {
    for (int i = 0; i < values.length; i++) {
        if (!values[i]) {
            return false;
        }
    }
    return true;
}

Key Insight: The second version is preferable in terms of performance, especially for large arrays. Its time complexity is ( $O (n)$ ) in the worst case (when all values are true), but it can terminate early, making it ( $O (k)$ ) where ( $k$ ) is the index of the first false value.

Concat Method

Description:

The concat method combines two arrays into a new array. This operation creates a new array of sufficient length to hold all elements from both input arrays, preserving their order. It’s a useful method since the length of an array can’t change. Notice, the function passes back a reference, not the value of the newly created array.

Method Signature:

int[] concat(int[] first, int[] second)

first: The first input array.
second: The second input array.
Returns: A new array containing the elements of first followed by the elements of second.

Example:

int[] arr1 = {1, 3};
int[] arr2 = {0, 2, 4};
int[] arr3 = concat(arr1, arr2);
// arr3 == {1, 3, 0, 2, 4}

Implementation:

int[] concat(int[] first, int[] second) {
    int[] result = new int[first.length + second.length];
    
    // Copy elements from the first array
    for (int i = 0; i < first.length; i++) {
        result[i] = first[i];
    }
 
    // Copy elements from the second array
    for (int i = 0; i < second.length; i++) {
        result[first.length + i] = second[i];
    }
 
    return result;
}

What Arrays Can’t Do in Java

Arrays are a useful and efficient way to store and manipulate collections of data in Java. However, there are several limitations and restrictions when it comes to working with arrays compared to some other data structures or languages. Below are some key limitations:

Arithmetic and Relational Operations

You cannot perform arithmetic or relational operations directly on arrays. For example:

Arithmetic operations like a1 + a2, a1 * a2, or a1 - a2 are not valid on arrays in Java. These operations are undefined, as Java doesn’t have built-in mechanisms for element-wise arithmetic like some other programming languages (such as Python or MATLAB).
Relational operations like a1 > a2, a1 == a2 are also invalid. Java does not support direct comparison between arrays using these operators. Arrays need to be compared element-wise, and the user has to implement logic for comparing arrays.

Example (Invalid Operation):

int[] arr1 = {1, 2, 3};
int[] arr2 = {4, 5, 6};
 
// Invalid: You cannot add or compare arrays directly in Java
int[] arr3 = arr1 + arr2;    // Compilation error
boolean result = arr1 > arr2; // Compilation error

Printing Arrays

When you try to print an array directly using System.out.println(), Java does not display the contents of the array. Instead, it prints the memory address or a reference to the array object, which isn’t helpful for debugging or visualization purposes.

Example (Attempt to Print an Array):

int[] arr1 = {3, 1, 3};
System.out.println(arr1);

Output:

[I@15db9742

This is because System.out.println(arr1) is calling the toString() method of the array object, which does not return the actual content of the array, but rather a string representation of its memory reference.

To print the contents of the array, you can use Arrays.toString():

Correct Way to Print an Array:

import java.util.Arrays;
 
int[] arr1 = {3, 1, 3};
System.out.println(Arrays.toString(arr1));

Output:

[3, 1, 3]

Alternatively, you can manually loop through the array to print the elements:

for (int i = 0; i < arr1.length; i++) {
    System.out.print(arr1[i] + " ");
}

3. Equality of Arrays

In Java, comparing arrays using == or .equals() does not work as expected. When using ==, you’re checking if the two array references point to the same memory location, not whether their elements are equal. Similarly, the equals() method inherited from Object does not compare arrays element-by-element, but compares their references.

Example (Incorrect Array Comparison):

int[] arr1 = {3, 1, 3};
int[] arr2 = {3, 1, 3};
 
if (arr1 == arr2) {
    System.out.println("Arrays are equal");
} else {
    System.out.println("Arrays are not equal");
}

Output:

Arrays are not equal

Even though both arrays have the same elements, arr1 == arr2 returns false because the two arrays are stored in different memory locations.

To compare arrays based on their content, use the Arrays.equals() method:

Correct Way to Compare Arrays:

import java.util.Arrays;
 
int[] arr1 = {3, 1, 3};
int[] arr2 = {3, 1, 3};
 
if (Arrays.equals(arr1, arr2)) {
    System.out.println("Arrays are equal");
} else {
    System.out.println("Arrays are not equal");
}

Output:

Arrays are equal

If you’re dealing with multidimensional arrays (like int[][]), you should use Arrays.deepEquals() to ensure proper comparison across all dimensions.

Methods from the Java Standard Library

Thankfully, the Java Standard Library provides utility methods to overcome these limitations. The java.util.Arrays class offers various static methods for common array manipulations:

Arrays.toString(): Converts an array into a human-readable string for printing.
```
System.out.println(Arrays.toString(arr));
```
Arrays.equals(): Compares two arrays element by element.
```
Arrays.equals(arr1, arr2);
```

Arrays.copyOf(): Creates a copy of an array.

int[] arrCopy = Arrays.copyOf(arr, arr.length);

Arrays.sort(): Sorts the elements of an array.
```
Arrays.sort(arr);
```
Arrays.fill(): Fills all elements of an array with a specific value.
```
Arrays.fill(arr, 5);
```

Arrays.deepEquals(): For comparing multidimensional arrays.

int[][] arr1 = {{1, 2}, {3, 4}};
int[][] arr2 = {{1, 2}, {3, 4}};
System.out.println(Arrays.deepEquals(arr1, arr2)); // true

Multidimensional Arrays

Declaration:

A multidimensional array in Java is essentially an array of arrays. The most commonly used form is the two-dimensional array, but Java supports arrays of any dimension.

Example Declaration (2D Array):

int[][] matrix = new int[3][4];  // A 3x4 matrix

This creates an array with 3 rows and 4 columns. Each element of the array is accessed using two indices: matrix[row][column].

You can also declare and initialize a 2D array in one line:

int[][] matrix = {
    {1, 2, 3, 4},
    {5, 6, 7, 8},
    {9, 10, 11, 12}
};

Example Declaration (3D Array):

Similarly, a 3D array is an array of 2D arrays:

int[][][] cube = new int[3][4][5]; // A 3x4x5 array (3 layers, each with 4 rows and 5 columns)

Memory Allocation in Java:

Multidimensional arrays in Java are stored as arrays of arrays. This means that the memory allocation for a multidimensional array is not contiguous (unlike languages such as C or C++). Each sub-array is a separate object stored in memory, and each of those objects can potentially be located at different places in the heap.

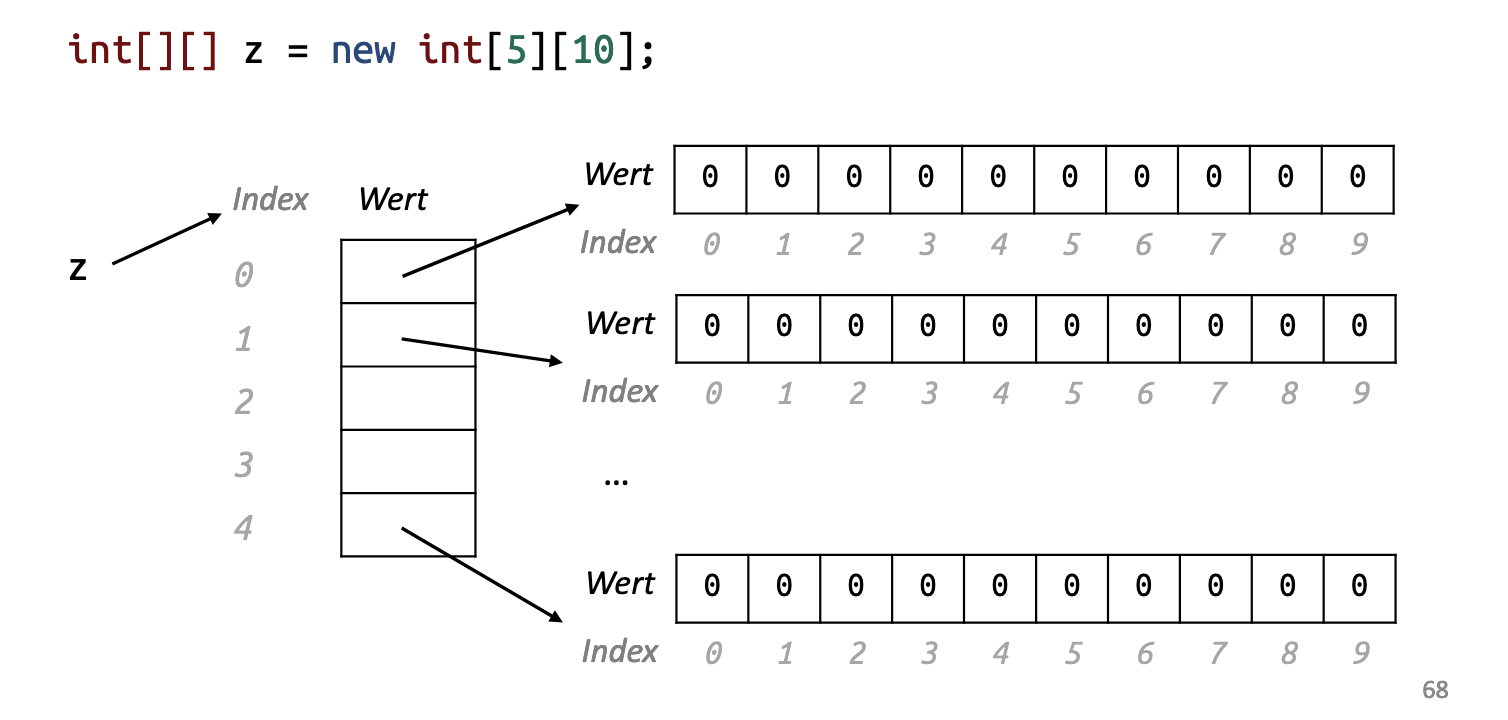
Memory Layout:

When you create a 2D array like int[][] matrix = new int[3][4];, Java allocates an array of 3 references (for the rows).
Each of these references points to an array of 4 integers (for the columns). Thus, the arrays of integers themselves are objects in memory.

This memory allocation scheme gives you flexibility. For example, the sub-arrays can have different lengths, allowing for the creation of jagged arrays:

int[][] jaggedArray = new int[3][];
jaggedArray[0] = new int[2]; // First row has 2 columns
jaggedArray[1] = new int[4]; // Second row has 4 columns
jaggedArray[2] = new int[3]; // Third row has 3 columns

Printing Multidimensional Arrays

When you try to print a multidimensional array using Arrays.toString(), you’ll notice that it only prints the memory references for the subarrays, rather than the actual elements. This is because Arrays.toString() works on one-dimensional arrays and treats the nested arrays as objects.

Example (Using `Arrays.toString()`):

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};
 
System.out.println(Arrays.toString(matrix)); // Incorrect way

Output:

[[I@15db9742, [I@6d06d69c, [I@7852e922]

This output displays the memory addresses of the subarrays rather than their contents.

Correct Way (Using `Arrays.deepToString()`):

To print a multidimensional array with its actual contents, use Arrays.deepToString(). This method is designed for nested arrays and prints all the elements, regardless of the depth of the array.

Example (Using Arrays.deepToString()):

import java.util.Arrays;
 
int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};
 
System.out.println(Arrays.deepToString(matrix)); // Correct way

Output:

[[1, 2, 3], [4, 5, 6], [7, 8, 9]]

Alternatively, you can manually print each element by looping through the rows and columns of the array.

Recursion

What is Recursion?

Recursion is a programming technique where a method calls itself to solve a smaller instance of the same problem. It involves breaking down a complex problem into simpler, more manageable sub-problems, and solving those sub-problems with the same function. The key idea is that each recursive call progresses towards a solution by reducing the size or complexity of the problem, eventually reaching a point where the problem is so simple that it can be solved directly—this is called the base case.

Recursion is commonly used in problems that have a natural hierarchical structure, such as tree traversal, mathematical sequences, or combinatorial problems like permutations and combinations.

EBNF vs. Math vs. Java

To understand recursion more clearly, let’s look at how it is represented in different contexts:

1. EBNF

In formal language theory, recursion is expressed in grammar rules. For example, a simple recursive grammar for a mathematical expression could be:

Expression ::= Number | Expression "+" Expression

This recursive definition specifies that an expression can either be a single number, or it can be the sum of two other expressions.

2. Mathematical Definition

In mathematics, recursion is used to define sequences or functions. For example, the factorial function (n!) is a classic recursive function:

n! = {1 n \times (n - 1)! if n = 0 if n > 0

This mathematical definition has two parts:

The base case: ( $0! = 1$ )
The recursive case: ( $n! = n \times (n - 1)!$ ) for ( $n > 0$ ).

3. Recursion in Java

In Java, recursion is implemented by having a method call itself within its body. The key to writing recursive methods is defining both a base case (when to stop the recursion) and a recursive case (how the problem is reduced in each recursive step).

Base Case vs Recursive Case

Base Case: This is the condition that stops the recursion. If not defined, the recursive function would call itself indefinitely, leading to a stack overflow error.
Recursive Case: This is where the function calls itself with modified arguments to progressively move towards the base case.

Example 1: Factorial in Java

Let’s implement the factorial function in Java.

public static int factorial(int n) {
    // Base case: factorial(0) = 1
    if (n == 0) {
        return 1;
    }
    // Recursive case: n! = n * (n-1)!
    else {
        return n * factorial(n - 1);
    }
}

Example 2: Counting Characters in a String

The following method counts how many times a character c appears in a given string s:

public static int count(char c, String s) {
    // Base case: if the string is empty, return 0
    if (s.length() == 0) {
        return 0;
    }
    // Recursive case: check if the first character matches
    else if (s.charAt(0) == c) {
        return 1 + count(c, s.substring(1));  // Add 1 and recurse
    }
    // If not, just recurse with the rest of the string
    else {
        return count(c, s.substring(1));
    }
}

Base Case: When the string is empty (s.length() == 0), the count is 0.
Recursive Case: The method checks the first character of the string. If it matches c, it adds 1 to the count and recurses on the rest of the string (s.substring(1)).

Example 3: Reverse a String

The following method recursively reverses a given string:

public static String reverse(String s) {
    // Base case: if the string has one or zero characters, return it as-is
    if (s.length() <= 1) {
        return s;
    }
    // Recursive case: reverse the rest of the string and add the first character at the end
    else {
        return reverse(s.substring(1)) + s.charAt(0);
    }
}

Base Case: If the string has length 1 or less, it is already reversed.
Recursive Case: It recursively reverses the substring without the first character, then appends the first character to the end.

Example 4: Enumerating Bitstrings

The following method generates all possible binary strings (bitstrings) of length n by recursively building prefixes:

public static void bitstrings(String prefix, int n) {
    // Base case: if the prefix length equals n, print it
    if (prefix.length() == n) {
        System.out.println(prefix);
    }
    // Recursive case: extend the prefix with '0' and '1' and recurse
    else {
        bitstrings(prefix + '0', n);
        bitstrings(prefix + '1', n);
    }
}

Base Case: When the length of the prefix matches n, it prints the bitstring.
Recursive Case: It adds ‘0’ and ‘1’ to the prefix, and recursively generates all bitstrings by exploring both options.

Usage Example:

public static void main(String[] args) {
    bitstrings("", 3);  // Outputs all 3-bit bitstrings
}

Output:

Call Stack

The call stack is a crucial part of how recursion (and method calls in general) works in programming languages like Java. It is a data structure used by the runtime environment to keep track of method calls, including the variables and state of each call. Whenever a method is called, a new frame is pushed onto the stack, and when a method completes, its frame is popped off.

In the context of recursion, the call stack keeps track of each recursive call, ensuring that when a base case is reached, the function can “unwind” correctly, returning to previous calls step by step.

How the Call Stack Works

Method Call: Every time a method is called (including recursive calls), a new stack frame is created. This frame contains:
- The method’s parameters
- Local variables
- The address of the next instruction to execute when the method returns (i.e., the point where the method was called).
Pushing onto the Stack: As each method is called, its frame is pushed onto the stack. If it’s a recursive method, multiple frames for the same method can exist at once, each with its own parameters and variables.
Base Case: When a base case is reached in a recursive function, the recursion stops. No further recursive calls are made, and the function begins to return its result.
Popping from the Stack: As each recursive call finishes, its frame is popped off the stack, and the control returns to the previous frame (the method that called it). This process continues until all recursive calls are resolved.

Example: Factorial and the Call Stack

Let’s take the recursive factorial function as an example to understand how the call stack operates.

public static int factorial(int n) {
    if (n == 0) {
        return 1; // Base case
    } else {
        return n * factorial(n - 1); // Recursive case
    }
}

If we call factorial(3), the sequence of calls and how they are handled in the call stack is as follows:

Call 1: factorial(3) is called.
- The result depends on factorial(2), so the method calls factorial(2), and a new frame for factorial(2) is pushed onto the stack.
Call 2: factorial(2) is called.
- This depends on factorial(1), so factorial(1) is called, and a new frame for factorial(1) is pushed onto the stack.
Call 3: factorial(1) is called.
- This depends on factorial(0), so factorial(0) is called, and a new frame for factorial(0) is pushed onto the stack.
Call 4: factorial(0) is called.
- This is the base case, so it returns 1. The frame for factorial(0) is popped from the stack.

Now, the function begins to return values as the stack unwinds:

Return to Call 3: factorial(1) returns 1 * 1 = 1, and its frame is popped.
Return to Call 2: factorial(2) returns 2 * 1 = 2, and its frame is popped.
Return to Call 1: factorial(3) returns 3 * 2 = 6, and its frame is popped.

The final result, 6, is returned to the caller of factorial(3).

Visualization of the Call Stack (Factorial Example)

Step 1: factorial(3) is called -> Stack: [factorial(3)]
Step 2: factorial(3) calls factorial(2) -> Stack: [factorial(3), factorial(2)]
Step 3: factorial(2) calls factorial(1) -> Stack: [factorial(3), factorial(2), factorial(1)]
Step 4: factorial(1) calls factorial(0) -> Stack: [factorial(3), factorial(2), factorial(1), factorial(0)]
Step 5: factorial(0) returns 1 -> Stack: [factorial(3), factorial(2), factorial(1)]
Step 6: factorial(1) returns 1 -> Stack: [factorial(3), factorial(2)]
Step 7: factorial(2) returns 2 -> Stack: [factorial(3)]
Step 8: factorial(3) returns 6 -> Stack: []

At the end, all the frames are popped from the stack, and the final result is obtained.

Stack Overflow in Recursion

One common problem with recursion is stack overflow. This happens when too many recursive calls are made without reaching the base case (either due to poor logic or an extremely deep recursion). Since each method call requires a new frame to be pushed onto the call stack, eventually, the stack may exceed its limit.

Example of Stack Overflow:

If you mistakenly write a recursive function without a proper base case or one that calls itself infinitely:

public static int infiniteRecursion(int n) {
    return infiniteRecursion(n); // Recursive call without a base case
}

Calling infiniteRecursion(1) will keep pushing new frames onto the stack without ever popping them off, eventually leading to a StackOverflowError.

Summary

Call Stack: A stack data structure used to manage method calls, including recursive calls.
Pushing and Popping: Each method call pushes a new frame onto the stack, and when the method returns, its frame is popped off.
Recursive Functions: In recursion, each call adds a new frame, and when the base case is reached, the stack unwinds as frames are popped in reverse order.
Stack Overflow: If recursion goes too deep without stopping, it can cause a stack overflow, crashing the program.

Continue here: 09 Solution Strategies, Logical Conclusions, Assertions, Hoare Logic

CS Notes

Explorer

08 Array Operations, Recursion

Arrays

Operations

Replace Method

Description:

Method Signature:

Example:

Implementation:

All True Method

Description:

Method Signature:

Example:

Implementation (Version 1):

Implementation (Version 2):

Concat Method

Description:

Method Signature:

Example:

Implementation:

What Arrays Can’t Do in Java

Arithmetic and Relational Operations

Printing Arrays

3. Equality of Arrays

Methods from the Java Standard Library

Multidimensional Arrays

Declaration:

Example Declaration (3D Array):

Memory Allocation in Java:

Memory Layout:

Printing Multidimensional Arrays

Example (Using Arrays.toString()):

Correct Way (Using Arrays.deepToString()):

Recursion

What is Recursion?

EBNF vs. Math vs. Java

1. EBNF

2. Mathematical Definition

3. Recursion in Java

Base Case vs Recursive Case

Example 1: Factorial in Java

Example 2: Counting Characters in a String

Example 3: Reverse a String

Example 4: Enumerating Bitstrings

Call Stack

How the Call Stack Works

Example: Factorial and the Call Stack

Visualization of the Call Stack (Factorial Example)

Stack Overflow in Recursion

Summary

Table of Contents

Backlinks

Example (Using `Arrays.toString()`):

Correct Way (Using `Arrays.deepToString()`):