11 Functions, Relations, Cardinality, Countability, Cantor's Diagonalization Argument

Lecture from: 23.10.2024 | Video: Videos ETHZ

Functions and Relations

Injective (One-to-one): A function f is injective if every element in its codomain is mapped to by at most one element in its domain. Formally, $x_1\ne x_2⟹f(x_1)\ne f(x_2)$ or it’s contrapositive $f(x_1)=f(x_2)⟹x_1=x_2$.

Surjective (Onto): A function f is surjective if every element in its codomain is mapped to by at least one element in its domain. Formally, for every $y$ in the codomain, there exists an $x$ in the domain such that $f(x)=y$.

Bijective (One-to-one and onto): A function f is bijective if it is both injective and surjective. A bijection establishes a one-to-one correspondence between the elements of its domain and codomain.

Composition of Injective Functions

If f and g are injective functions, then their composition $g\circ f$ is also injective.

Proof (Lecture)

To show that $g\circ f$ is injective, we start with two distinct elements, $a$ and $a^{\prime }$, from the domain of $f$ (and hence, the domain of $g\circ f$).

1. f is injective: Since $f$ is injective, we know that if $a\ne a^{\prime }$, then $f(a)\ne f(a^{\prime })$.
2. g is injective: Because g is injective, if $f(a)\ne f(a^{\prime })$, then $g(f(a))\ne g(f(a^{\prime }))$.
3. Composition: By the definition of function composition, $(g\circ f)(a)=g(f(a))$ and $(g\circ f)(a^{\prime })=g(f(a^{\prime }))$.
4. Putting it Together: Combining these steps, we conclude that if $a\ne a^{\prime }$, then $(g\circ f)(a)\ne (g\circ f)(a^{\prime })$. This is the definition of injectivity for the composition, so $g\circ f$ is injective.

Proof (Contrapositive)

To show that $g\circ f$ is injective, we’ll prove the contrapositive statement: if $(g\circ f)(x_1)=(g\circ f)(x_2)$, then $x_1=x_2$. This is equivalent to showing that if $x_1\ne x_2$, then $(g\circ f)(x_1)\ne (g\circ f)(x_2)$.

1. Assume Inequality: Let $x_1\ne x_2$ for some $x_1,x_2\in A$.
2. f Injective: Since f is injective, $x_1\ne x_2$ implies $f(x_1)\ne f(x_2)$.
3. g Injective: Since g is injective, $f(x_1)\ne f(x_2)$ implies $g(f(x_1))\ne g(f(x_2))$.
4. Composition: By definition of composition, $(g\circ f)(x_1)=g(f(x_1))$ and $(g\circ f)(x_2)=g(f(x_2))$.
5. Conclusion: Combining these steps, we have shown that if $x_1\ne x_2$, then $(g\circ f)(x_1)\ne (g\circ f)(x_2)$. This proves the contrapositive statement, so $g\circ f$ is injective.

Composition of Surjective Functions

If f and g are surjective functions, then their composition $g\circ f$ is also surjective.

Proof (Contrapositive)

To prove the contrapositive, we’ll show that if $g\circ f$ is not surjective, then either f or g is not surjective.

1. Assume Not Surjective: Suppose $g\circ f$ is not surjective. This means there exists an element $c$ in the codomain of $g\circ f$ (which is the codomain of g) that is not mapped to by any element in the domain of $g\circ f$ (which is the domain of f).
2. No Preimage: There is no $a$ in the domain of $f$ such that $(g\circ f)(a)=c$. This means there is no a such that $g(f(a))=c$.
3. g Not Surjective or f Not Surjective:
   • If g is not surjective: Then there is no element $b$ in the domain of g such that $g(b)=c$. Since f maps to the domain of g, there cannot be an a in the domain of f such that $f(a)=b$ that would lead to $g(f(a))=c$. So, in this case, g is not surjective.
   • If g is surjective: Since g is surjective, there exists some b in the domain of g such that $g(b)=c$. But because there’s no a in the domain of f such that $g(f(a))=c$, this means there’s no a such that $f(a)=b$. So, in this case, f is not surjective.
4. Conclusion: We’ve shown that if $g\circ f$ is not surjective, then either g or f must not be surjective. This proves the contrapositive, so the composition of two surjective functions is surjective.

Composition of Bijective Functions

If f and g are bijective functions, then their composition $g\circ f$ is also bijective.

Proof: We can prove this directly using the previous lemmas for injective and surjective compositions.

1. Injective: Since f and g are bijective (and hence injective), we know from the previous lemma that $g\circ f$ is also injective.
2. Surjective: Since f and g are bijective (and hence surjective), we know from the previous lemma that $g\circ f$ is also surjective.
3. Conclusion: Because $g\circ f$ is both injective and surjective, it is bijective.

Cardinality: Comparing the Sizes of Sets

This section introduces the concept of cardinality, which allows us to compare the sizes of sets even if they contain infinitely many elements.

Definitions

1. Equal Cardinality: Two sets, A and B, have equal cardinality, denoted by $A\sim B$, if there exists a bijection between them. A bijection is a function that is both injective (one-to-one) and surjective (onto). This implies that there is a perfect pairing of elements between the two sets.

2. Preorder (Less Than or Equal to in Cardinality): Set A has cardinality less than or equal to set B, denoted by $A⪯B$, if there exists an injection from A to B. An injection is a one-to-one function, meaning each element in A is mapped to a unique element in B. This implies that B has at least as many elements as A.

3. Strict Smaller: We say that A has strictly smaller cardinality than B, denoted by $A\prec B$, if $A⪯B$ and $A\nsim B$. In other words, there’s an injection from A to B, but there’s no bijection.

Properties of Cardinality Relations (Lemma 3.15)

This lemma establishes key properties of the cardinality relations we’ve defined: equal cardinality ($\sim$) and preorder ($⪯$).

1. Equal Cardinality is an Equivalence Relation:
   • Reflexive: A set A is trivially equivalent to itself ($A\sim A$) because the identity function on A is a bijection. The identity function maps each element of A to itself, establishing a one-to-one correspondence.
   • Symmetric: If $A\sim B$, then there exists a bijection f from A to B. Since f is a bijection, its inverse, denoted by $f^{-1}$, is also a bijection. The inverse function maps each element in B back to its unique preimage in A. Therefore, $B\sim A$.
   • Transitive: If $A\sim B$ and $B\sim C$, then there exist bijections $f:A\to B$ and $g:B\to C$. The composition $g\circ f:A\to C$ is also a bijection (as we proved earlier). Therefore, $A\sim C$.
2. Preorder is Transitive:
   • Proof: If $A⪯B$ and $B⪯C$, then there exist injections $f:A\to B$ and $g:B\to C$. The composition $g\circ f:A\to C$ is an injection (as we proved earlier). Therefore, $A⪯C$.
3. Subset Implies Preorder: If $A\subseteq B$, then $A⪯B$.
   • Proof: The identity function restricted to A, denoted by $i_A:A\to A$, is an injection. Since $A\subseteq B$, we can consider $i_A$ as a function from A to B, and it remains an injection. Therefore, $A⪯B$.

• Equal Cardinality ($\sim$) is an equivalence relation, which means it partitions sets into equivalence classes where sets within the same class have the same cardinality.
• Preorder ($⪯$) is a transitive relation, meaning if A has cardinality less than or equal to B and B has cardinality less than or equal to C, then A has cardinality less than or equal to C.
• Subset Implication: If A is a subset of B, then A has cardinality less than or equal to B.

Cardinal Preorder Both Ways Implies Equivalence (Theorem)

If $A⪯B$ and $B⪯A$, then $A\sim B$.

This theorem, known as the Cantor-Bernstein-Schroeder Theorem, is a fundamental result in set theory. It states that if there are injections from A to B and from B to A, then there must also be a bijection between A and B. This implies that the two sets have the same cardinality.

The proof of this theorem is non-trivial and involves constructing a bijection from a series of injections. However, the theorem itself provides a powerful tool for comparing the sizes of sets.

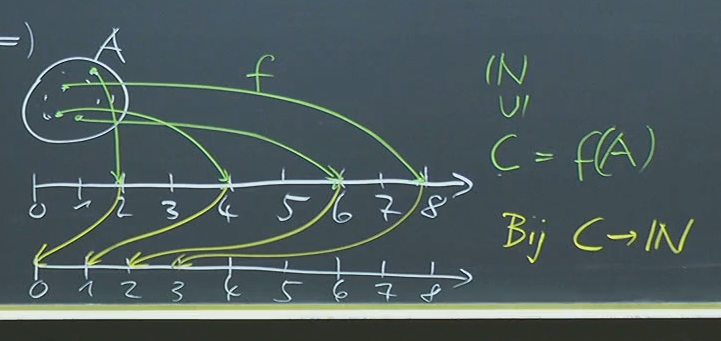
Countability (Theorem 3.17)

A set A is countable if and only if A is finite or A has the same cardinality as the natural numbers ($A\sim \mathbb{N}$).

Proof:

• ($\Leftarrow$): If A is finite or $A\sim \mathbb{N}$, then A is countable by definition. In the finite case, the identity function on A suffices. In the infinite case, the bijection between A and $\mathbb{N}$ provides the required mapping.
• ($\Rightarrow$): If A is countable and infinite, there exists a surjection from $\mathbb{N}$ to A. Using the well-ordering principle (explained below), we can construct an injection from A to $\mathbb{N}$. Since we have a surjection from $\mathbb{N}$ to A and an injection from A to $\mathbb{N}$, by the Cantor-Bernstein-Schroeder theorem, we have $A\sim \mathbb{N}$.

The Well-Ordering Principle

The well-ordering principle states that every non-empty subset of the natural numbers has a least element. This principle is crucial for proving the countability theorem and other results.

Hilberts Hotel:

Examples of Countable Sets

Example 1: Finite Bitstrings

The set of all finite bitstrings, denoted $\{0,1{\}}^{\ast }$, is countable.

Proof:

Although each bitstring corresponds to a natural number via binary representation, this doesn’t directly establish countability because different bitstrings can represent the same number (e.g., “010” and “0010” both represent 2).

To address this issue, we construct an injection from $\{0,1{\}}^{\ast }$ to $\mathbb{N}$. Consider the function $z^{\prime }(1||a)$, which prepends a ‘1’ to the bitstring a before converting it to a decimal number. This ensures that each bitstring maps to a unique natural number. Since we have an injection from $\{0,1{\}}^{\ast }$ to $\mathbb{N}$, and $\mathbb{N}$ is well-ordered, we can construct a bijection using the well-ordering principle, establishing that $\{0,1{\}}^{\ast }\sim \mathbb{N}$.

Example 2: $\mathbb{N}\times \mathbb{N}$

The Cartesian product $\mathbb{N}\times \mathbb{N}$ is countable. We can demonstrate this using bitstrings.

Proof:

We aim to show $\{0,1{\}}^{\ast }\times \{0,1{\}}^{\ast }\sim \{0,1{\}}^{\ast }$. A naive concatenation of bitstrings, like $(010,100)\to 010100$, is insufficient because it is not unique and therefore not injective. A computer science perspective on this is whether the resulting bitstring can be uniquely parsed back into its original components. Simple concatenation lacks this property.

Instead, we can use a different encoding: $(a,b)\mapsto 0^{|a|}1ab$ where $|a|$ is the length of bitstring a. This encoding is injective, meaning each pair of bitstrings maps to a unique single bitstring. Since finite bitstrings are countable, this establishes that $\mathbb{N}\times \mathbb{N}\sim \mathbb{N}$.

Theorems on Countability

Cartesian Product of Countable Sets (Corollary 3.20)

The Cartesian product $A\times B$ of two countable sets $A$ and $B$ is countable, i.e., $A⪯\mathbb{N}\wedge B⪯\mathbb{N}⟹A\times B⪯\mathbb{N}$.

Proof:

We first prove $A\times B⪯\mathbb{N}\times \mathbb{N}$ by exhibiting an injection $g:A\times B\to \mathbb{N}\times \mathbb{N}$, namely $g(a,b)=(f_1(a),f_2(b))$. That $g$ is an injection can be proved as follows:

$(a,b)\ne (a^{\prime },b^{\prime })⟹a\ne a^{\prime }\vee b\ne b^{\prime }⟹f_1(a)\ne f_1(a^{\prime })\vee f_2(b)\ne f_2(b^{\prime })⟹(f_1(a),f_2(b))\ne (f_1(a^{\prime }),f_{2(b^{\prime }))}$

The first implication follows from the definition of pairs, the second implication from the fact that $f_1$ and $f_2$ are injections, and the last implication from the definition of pairs again.

Using $A\times B⪯\mathbb{N}\times \mathbb{N}$ (just proved) and $\mathbb{N}\times \mathbb{N}⪯\mathbb{N}$ now gives $A\times B⪯\mathbb{N}$ because $⪯$ is transitive.

Countability of Cartesian Products and Finite Sequences (Theorem 3.22)

This section explores the countability of sets constructed from countable sets using Cartesian products and the (Kleene) star operation.

Let $A$ and $A_i$, for $i\in \mathbb{N}$, be countable sets. The following holds:

(i) Finite Cartesian Powers: For any $n\in \mathbb{N}$, the set $A^n$ (the set of all $n$-tuples of elements from $A$) is countable. (ii) Countable Union of Countable Sets: The union ${\bigcup }_{i\in \mathbb{N}}{A}_i$ of a countable list $A_0,A_1,A_2,...$ of countable sets is countable. (iii) Kleene Star: The set $A^{\ast }$ (the set of all finite sequences of elements from $A$) is countable.

Proof of (i) - Finite Cartesian Powers

Proof (by induction on n):

• Base Case (n = 1): $A^1=A$, which is countable by assumption.
• Inductive Hypothesis: Assume $A^k$ is countable for some $k\ge 1$.
• Inductive Step: We need to show that $A^{k+1}$ is countable. We know $A^{k+1}=A^k\times A$. Since $A^k$ and $A$ are countable (by the inductive hypothesis and the initial assumption, respectively), their Cartesian product $A^{k+1}$ is countable by Corollary 3.20.
• Conclusion: By induction, $A^n$ is countable for all finite $n$.

Proof of (ii) - Countable Union of Countable Sets (not part of script)

I suggest you look at proof of (iii) since that automatically shows how you’d prove (ii) elegantly. Otherwise check out the proof below.

Proof:

Since each $A_i$ is countable, there exists a surjection $f_i:\mathbb{N}\to A_i$. Let’s construct a function $g:\mathbb{N}\times \mathbb{N}\to {\bigcup }_{i\in \mathbb{N}}{A}_i$ as follows: $g(i,j)=f_i(j)$

This means that the $(i,j)$-th element of $\mathbb{N}\times \mathbb{N}$ maps to the $j$-th element of $A_i$. This mapping is surjective because for any element $a\in {\bigcup }_{i\in \mathbb{N}}{A}_i$, there is some $i$ for which $a\in A_i$, and because $f_i$ is a surjection, there exists some $j$ for which $f_i(j)=a$. Therefore, $g(i,j)=a$.

Since $\mathbb{N}\times \mathbb{N}$ is countable, there exists a bijection $h:\mathbb{N}\to \mathbb{N}\times \mathbb{N}$. Composing $h$ with $g$, we get a surjection $g\circ h:\mathbb{N}\to {\bigcup }_{i\in \mathbb{N}}{A}_i$. Therefore, ${\bigcup }_{i\in \mathbb{N}}{A}_i$ is countable by Theorem 3.17.

Proof of (iii) - Kleene Star

Proof:

1. Injection from $A$ to Bitstrings: Since $A$ is countable ($A⪯\mathbb{N}$), there exists an injection from $A$ to $\mathbb{N}$. Because finite bitstrings ($\{0,1{\}}^{\ast }$) are countable and in bijection with the natural numbers, we can represent each element of $A$ as a unique finite bitstring via a suitable injection $f:A\to \{0,1{\}}^{\ast }$.

2. Injection from $A^{\ast }$ to Bitstrings: We now construct an injection $g:A^{\ast }\to \{0,1{\}}^{\ast }$. Given a finite sequence $(a_1,a_2,...,a_n)\in A^{\ast }$, we encode it as a bitstring using the injection f from step 1 and a cleverly chosen separator: $(a_1,a_2,\dots ,a_n)\mapsto f(a_1)11f(a_2)11\dots 11f(a_n)$ where each $f(a_i)$ is the unique bitstring representation of $a_i$ (e.g. $0\mapsto 00$ and $1\mapsto 01$, and “11” serves as a delimiter between elements of the sequence.

3. Uniqueness of Decoding: This encoding is injective. Given the encoded bitstring, we can uniquely decompose it back to the original sequence because the delimiter “11” allows us to distinguish where one element ends and the next begins. The individual $f(a_i)$ are unique from the first injection, and since we can parse the overall sequence we can uniquely reconstruct it.

4. Countability: Since we have an injection from $A^{\ast }$ to $\{0,1{\}}^{\ast }$ and $\{0,1{\}}^{\ast }$ is countable, we conclude that $A^{\ast }⪯\mathbb{N}$, which means $A^{\ast }$ is countable.

Example: Let $A=\{a,b,c\}$. Suppose we have the injection $f:A\to \{0,1{\}}^{\ast }$ defined as $f(a)=00$, $f(b)=01$, and $f(c)=10$. Then the sequence $(b,a,c,b)$ would be encoded as the bitstring $01110011101101$.

Theorem 3.22 demonstrates that countability is preserved under finite Cartesian products and the Kleene star operation. This allows us to reason about the countability of complex structures built from countable sets.

The Uncountability of Infinite Binary Sequences (Cantor’s Diagonalization Argument)

Theorem: The set of all infinite binary sequences, denoted as $\{0,1{\}}^{\infty }$, is uncountable.

Proof

This proof employs proof by contradiction. We begin by assuming that the set of all infinite binary sequences is countable. This assumption will lead to a logical contradiction, proving that our initial assumption must be false.

1. Assume Countability: Assume that there exists a bijection $f:\mathbb{N}\to \{0,1{\}}^{\infty }$. A bijection means that each natural number n maps to a unique infinite binary sequence, and conversely, each infinite binary sequence is mapped to by a unique natural number.

2. Representation: We can represent each infinite binary sequence $f(i)$ as an infinite list of bits: $f(i)={\beta }_{i,0},{\beta }_{i,1},{\beta }_{i,2},{\beta }_{i,3},...$ where ${\beta }_{i,j}$ is the $j$-th bit in the $i$-th sequence. For convenience, we begin numbering the bits starting from $j=0$.

3. Construct a New Sequence: Let $\overline{b}$ denote the complement of a bit $b\in \{0,1\}$ (if $b=0$, then $\overline{b}=1$, and if $b=1$, then $\overline{b}=0$). Now, define a new infinite binary sequence $\alpha$ as follows: $\alpha =\overline{{\beta }_{0,0}},\overline{{\beta }_{1,1}},\overline{{\beta }_{2,2}},\overline{{\beta }_{3,3}},...$ 4. Contradiction:

• Existence: Clearly, $\alpha$ is an infinite binary sequence and therefore belongs to the set $\{0,1{\}}^{\infty }$.
• Uniqueness: However, there cannot exist any natural number $n\in \mathbb{N}$ such that $\alpha =f(n)$. This is because $\alpha$ is constructed to differ from $f(n)$ in at least one bit (actually the $n$-th bit) for every natural number $n$.

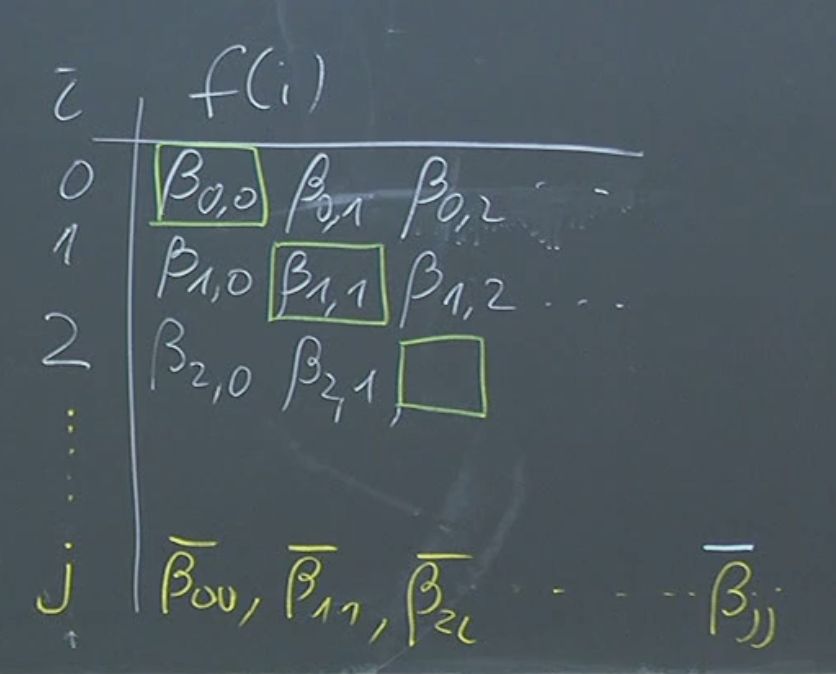
5. Conclusion:

The existence of $\alpha$, which does not correspond to any natural number under the supposed bijection f, contradicts our initial assumption that f is a bijection. This contradiction forces us to reject our initial assumption that the set of infinite binary sequences is countable. Therefore, $\{0,1{\}}^{\infty }$ must be uncountable.

Relationship to Programs and Functions

This result has profound implications for the relationship between computer programs and mathematical functions.

• Finite Programs: Computer programs are fundamentally finite sequences of instructions. They can be represented as finite strings of symbols (like bitstrings). Therefore, the set of all possible computer programs is countable (similar to the set of finite bitstrings ${0,1}^{\ast }$).

• Infinite Functions: The set of all possible functions, even just from $\mathbb{N}$ to $0,1$, is uncountable (as shown by the diagonalization argument above). This is because the space of infinite sequences ${0,1}^{\infty }$ is a representation of all such functions. For example, consider the function that maps each natural number n to its $n$-th bit in the binary representation of the number $\pi$. This is a function from $\mathbb{N}$ to $0,1$, and there is no way to represent it with a finite program.

• Uncomputable Functions: Since the set of all possible functions is uncountable, but the set of all possible computer programs is countable, there must exist functions that cannot be computed by any finite program. These functions are known as uncomputable functions.

Example: The Halting Problem is a classic example of an uncomputable function. The Halting Problem asks if, given a program P and its input I, whether the program P will eventually halt when run with input I. It has been proven that no finite computer program can solve the Halting Problem for all possible programs and inputs.

Uncountability of Real Numbers

The same diagonalization technique can be used to show that the interval $[0,1]$ (and hence the set of real numbers $\mathbb{R}$ itself (see [[10 Posets, Hasse Diagrams, Lexicographical Ordering, Special Elements, Functions, Countability, Infinities#example-01-sim-mathbbr|Example $(0,1)simmathbbR$]])) is uncountable. This is achieved by interpreting the elements of $\{0,1{\}}^{\infty }$ as the binary expansion of a real number in the interval $[0,1]$. This establishes a one-to-one correspondence between infinite binary sequences and real numbers in $[0,1]$. Since the set of infinite binary sequences is uncountable, the interval $[0,1]$ must also be uncountable.

Key Takeaway

The uncountability of infinite bitstrings (and by extension, the set of all functions) highlights the fundamental limitations of finite computational systems. It demonstrates that there are inherently uncomputable functions, meaning there are mathematical problems that cannot be solved by any finite program.

Continue here: 12 Cardinality, Number Theory, Rings, Euclidian Rings, Ideal, Congruence, Modular Arithmetic, Diophantine Equations