18 Rings, Fields, Real Polynomial Fields, Polynomial Fields, Galois Fields

Lecture from: 18.11.2024 | Video: Videos ETHZ

Rings

Recall from last time…

A ring $⟨R;+,-,0,\cdot ,1⟩$ is an algebraic structure with two binary operations, addition ($+$) and multiplication ($\cdot$), and specific elements $0$ and $1$ that act as additive and multiplicative identities, respectively.

Key Properties:

1. Additive Abelian Group: $⟨R;+,-,0⟩$ forms an abelian (commutative) group.
2. Multiplicative Monoid: $⟨R;\cdot ,1⟩$ forms a monoid. Note: $1$ can equal $0$ only in the trivial ring with one element.
3. Distributivity: Multiplication distributes over addition both from the left and the right: $a\cdot (b+c)=(a\cdot b)+(a\cdot c)$ and $(a+b)\cdot c=(a\cdot c)+(b\cdot c)$.

Important Lemmas:

• $0\cdot a=0$ for all $a\in R$.
• $(-a)\cdot b=-(a\cdot b)$ for all $a,b\in R$.
• If $|R|\ge 2$, then $1\ne 0$. This ensures that the multiplicative identity is distinct from the additive identity in non-trivial rings.

Special Types of Rings:

• Integral Domain: A commutative ring with $1\ne 0$ and no zero divisors. A zero divisor is a non-zero element $a$ such that there exists a non-zero $b$ with $a\cdot b=0$. Integral domains have the cancellation property: if $ab=ac$ and $a\ne 0$, then $b=c$.

Important Elements within a Ring:

• Units (denoted by $R^{\ast }$): Elements with multiplicative inverses within the ring. The set of units, $R^{\ast }$, forms a group under multiplication called the group of units.
• Irreducible Elements: Analogous to prime numbers in integers. A non-zero, non-unit element $p$ is irreducible if $p=ab$ implies either $a$ or $b$ is a unit.

Examples of Rings and their Groups of Units:

• $\mathbb{Z}$ (Integers): An integral domain. ${\mathbb{Z}}^{\ast }=\{1,-1\}$.
• $\mathbb{R}$ (Real Numbers): A field. ${\mathbb{R}}^{\ast }=\mathbb{R}\setminus \{0\}$.
• $\mathbb{Z}[i]$ (Gaussian Integers): An integral domain. $\mathbb{Z}[i{]}^{\ast }=\{1,-1,i,-i\}$. Divisibility is determined using the norm $N(a+bi)=a^2+b^2$.
• ${\mathbb{Z}}_m$ (Integers Modulo m): A ring. ${\mathbb{Z}}_m^{\ast }$ consists of elements coprime to $m$. Has zero divisors if $m$ is not prime.
• $R[x]$ (Polynomial Rings): The ring of polynomials with coefficients in a ring $R$. $(R[x]{)}^{\ast }=R^{\ast }$ (i.e., the units of the polynomial ring are the units of the underlying ring $R$, viewed as constant polynomials.) If $R$ is a field, then $(R[x]{)}^{\ast }=R^{\ast }=R\setminus \{0\}$.

Fields

A field is a commutative ring $⟨F;+,-,0,\cdot ,1⟩$ where $1\ne 0$ and every non-zero element has a multiplicative inverse. In other words, the set of units, $F^{\ast }$, is equal to $F\setminus \{0\}$. This means for every $a\in F$ such that $a\ne 0$, there exists an element $a^{-1}\in F$ such that $a\cdot a^{-1}=a^{-1}\cdot a=1$.

This requirement for multiplicative inverses for all non-zero elements makes fields particularly well-suited for algebraic manipulations, as division (except by zero) is always possible.

Key Properties of Fields:

• Commutativity: Both addition and multiplication are commutative.
• No Zero Divisors: If $a\cdot b=0$, then either $a=0$ or $b=0$. This property follows directly from the existence of multiplicative inverses for non-zero elements. If $a\cdot b=0$ and $a\ne 0$, then multiplying both sides by $a^{-1}$ yields $b=0$.
• Cancellation Property: If $a\cdot b=a\cdot c$ and $a\ne 0$, then $b=c$.
• Solutions to Linear Equations: Equations of the form $ax+b=c$ always have a unique solution $x=a^{-1}(c-b)$, provided $a\ne 0$.

Examples of Fields:

• $\mathbb{Q}$ (Rational Numbers): The field of rational numbers is formed by fractions $\frac{p}{q}$, where $p$ and $q$ are integers and $q\ne 0$.
• $\mathbb{R}$ (Real Numbers): The field of real numbers includes all rational and irrational numbers.
• $\mathbb{C}$ (Complex Numbers): The field of complex numbers is formed by numbers of the form $a+bi$, where $a$ and $b$ are real numbers and $i^2=-1$.
• ${\mathbb{Z}}_p$ (Integers Modulo $p$ where $p$ is prime): When $p$ is a prime number, every non-zero element in ${\mathbb{Z}}_p$ has a multiplicative inverse modulo $p$. This makes ${\mathbb{Z}}_p$ a finite field. If $p$ is not prime then ${\mathbb{Z}}_p$ has zero divisors.
• Finite Fields (Galois Fields): There exist finite fields other than ${\mathbb{Z}}_p$. These are called Galois fields and are denoted as $GF(p^n)$, where $p$ is prime and $n$ is a positive integer. These are crucial in cryptography, coding theory, and other areas. $GF(p)$ is equivalent to ${\mathbb{Z}}_p$, though usually $GF(q)$ denotes finite fields with $|GF(q)|=q$ elements, where $q$ can be a prime number or prime to the power of $n$, which is a natural number without zero. $n=1$ gets us back to ${\mathbb{Z}}_p$.

Non-Examples:

• $\mathbb{Z}$ (Integers): Not a field because most integers do not have multiplicative inverses within $\mathbb{Z}$. For example, 2 does not have a multiplicative inverse within the integers.
• ${\mathbb{Z}}_m$ (Integers Modulo $m$ where $m$ is composite): Not a field. For example ${\mathbb{Z}}_6$ is not a field since not every non-zero element has an inverse with respect to multiplication in ${\mathbb{Z}}_6$. $2\cdot x\equiv 1(\mathrm{mod}6)$ has no solution.

Fields are fundamental structures in abstract algebra and have wide-ranging applications in many areas of mathematics and computer science.

Secret Sharing with Polynomials

One application of abstract algebra, specifically fields, is secret sharing. Secret sharing schemes allow distributing a secret among multiple parties so that only authorized combinations of parties can reconstruct the secret. Here’s a simple example using a polynomial over a field:

Suppose we want to share a secret $S$ among 4 people. We can construct a polynomial of degree 3:

$P(x)=a_3{x}^3+a_2{x}^2+a_{1}x+a_0$

where $a_0=S$ is our secret. The coefficients $a_1,a_2,a_3$ are randomly chosen from the field we are working over.

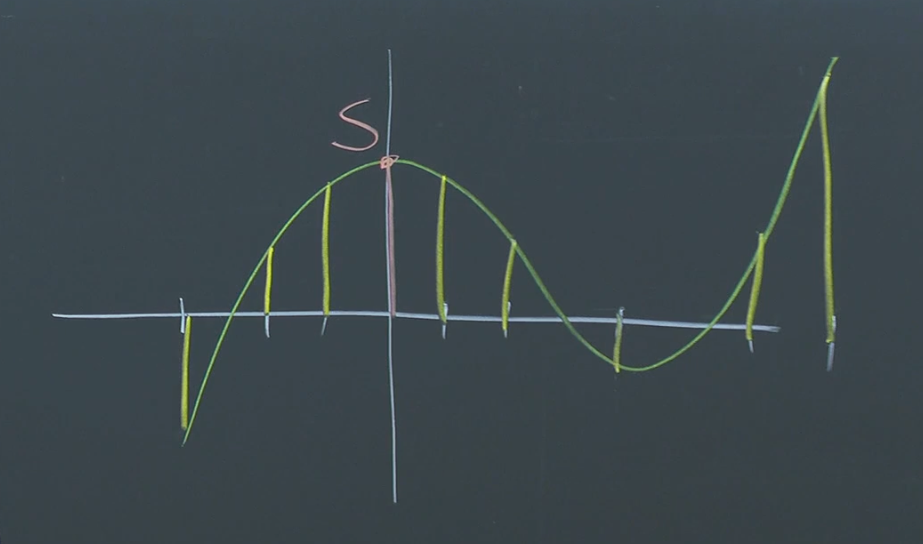
We then evaluate the polynomial at four distinct non-zero $x$-values (e.g., 1, 2, 3, 4) and distribute these points (shares) to the four people. Each person receives a pair $(x_i,P(x_i))$, represented by the yellow lines in the graph.

Polynomial Interpolation:

The key to this scheme is polynomial interpolation. Given any four points on the polynomial, we can uniquely reconstruct the entire polynomial, including the secret $S=P(0)$. This is because a polynomial of degree $n$ is uniquely determined by $n+1$ points. Lagrange interpolation is a common technique for reconstructing the polynomial.

Why Fields are Essential:

Fields are crucial for this scheme to work because they guarantee the existence of multiplicative inverses for non-zero elements. This is essential for Lagrange interpolation and other methods for reconstructing the polynomial from its shares. Without inverses, we might encounter situations where the necessary calculations are not possible. We’ll learn more on this later…

Security:

Any three or fewer people cannot determine the secret. With only three points, there are infinitely many polynomials of degree 3 that pass through those points, each with a different value at $x=0$. This means that any guess for the secret is equally likely, providing no information about the actual secret.

For example, those 3 people know where the polynomial is at their x-values, however they don’t know where the constant part is (S). There exist infinitely many polynomials passing through these 3 lines, all with different intercepts at $x=0$. Therefore those three people alone cannot gain any information about the constant term.

Practical Considerations (Finite Fields):

In computer science, we typically work with finite fields rather than infinite fields like real numbers. This is because computers have finite precision and cannot represent arbitrary real numbers exactly. Finite fields provide a suitable algebraic structure for secret sharing and other cryptographic applications on computers.

Quaternion Numbers

William Rowan Hamilton sought a way to extend the geometric interpretation of complex numbers, which represent rotations and scaling in the 2D plane, to three dimensions. He specifically wanted a number system that could represent rotations in 3D space analogously to how complex numbers handle rotations in 2D.

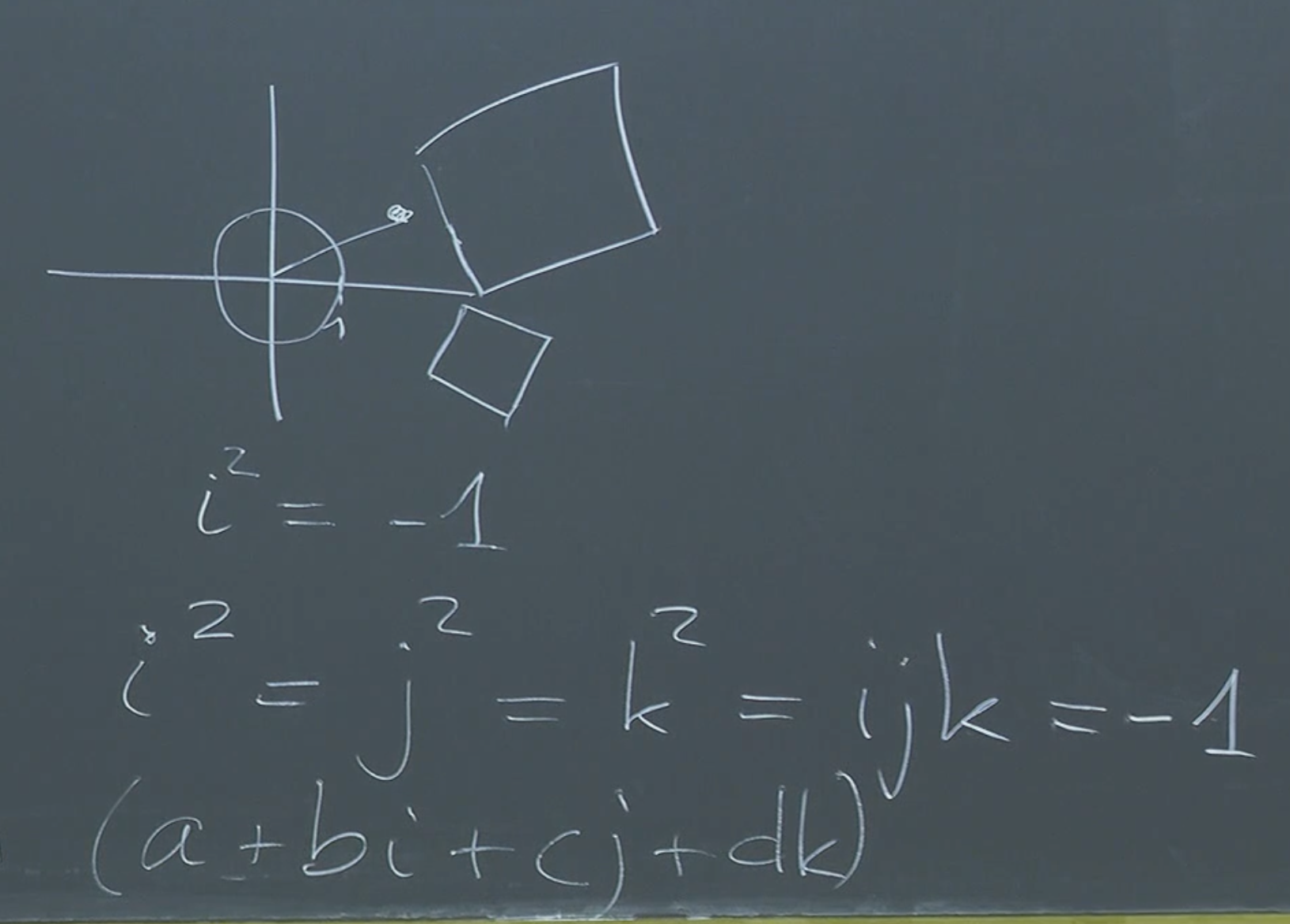
Complex numbers can be visualized as points in the 2D plane. Multiplying a complex number by another complex number corresponds to a rotation and scaling in the plane. The norm (magnitude) of the product is the product of the norms.

This system of quaternions, denoted by $\mathbb{H}$, forms a ring. Interestingly, every non-zero element in $\mathbb{H}$ has a multiplicative inverse, meaning ${\mathbb{H}}^{\ast }=\mathbb{H}\setminus \{0\}$. This makes $\mathbb{H}$ similar to a field, but crucially, quaternion multiplication is not commutative.

Structures that satisfy all the field axioms except for the commutativity of multiplication are called division rings or skew fields (Schiefkörper in German). The lack of commutativity in quaternion multiplication, while essential for its ability to represent 3D rotations, makes it less convenient for certain algebraic manipulations compared to fields. For our purposes in this course, the non-commutativity of $\mathbb{H}$ makes it less suitable than fields, so we’ll primarily focus on fields.

The set $\{1,-1,i,-i,j,-j,k,-k\}$ under quaternion multiplication forms a group called the quaternion group, denoted $Q_8$. It’s a non-abelian group of order 8. This is a subset of the quaternions and forms a group, but it is not the full set of quaternions $\mathbb{H}$, which is a ring (and a division ring/skew field). $Q_8$ is closed under multiplication and inverses and provides a concrete example of a non-commutative group. This was the last group of order 8 we hadn’t found yet…

Theorem: A Field is an Integral Domain

Theorem: Every field is an integral domain.

Proof:

1. Definition of Field: A field is a commutative ring $⟨F;+,-,0,\cdot ,1⟩$ where $1\ne 0$ and every non-zero element has a multiplicative inverse.

2. Definition of Integral Domain: An integral domain is a commutative ring $⟨R;+,-,0,\cdot ,1⟩$ with $1\ne 0$ and no zero divisors. This means if $a\cdot b=0$, then either $a=0$ or $b=0$.

3. Showing No Zero Divisors: Let $F$ be a field. We need to show that $F$ has no zero divisors. Suppose $a,b\in F$ and $a\cdot b=0$.

4. Case 1: $a=0$. If $a=0$, then the condition for no zero divisors is satisfied.

5. Case 2: $a\ne 0$. If $a\ne 0$, then $a$ has a multiplicative inverse $a^{-1}\in F$. We can multiply both sides of $a\cdot b=0$ by $a^{-1}$: $a^{-1}\cdot (a\cdot b)=a^{-1}\cdot 0$ $(a^{-1}\cdot a)\cdot b=0$ (Associativity) $1\cdot b=0$ $b=0$

6. Conclusion: In both cases, either $a=0$ or $b=0$. Therefore, $F$ has no zero divisors.

7. Final Statement: Since $F$ is a commutative ring with $1\ne 0$ and no zero divisors, $F$ is an integral domain.

Therefore, every field is an integral domain. The converse is not necessarily true; integral domains are not always fields. For example, $\mathbb{Z}$ is an integral domain but not a field, as integers other than 1 and -1 do not have multiplicative inverses within $\mathbb{Z}$.

Galois Fields (Finite Fields)

Recall that ${\mathbb{Z}}_m$, the integers modulo $m$, forms a ring. However, it’s a field if and only if $m$ is a prime number. This is because if $m$ is prime, every non-zero element in ${\mathbb{Z}}_m$ has a multiplicative inverse modulo $m$. In other words, for any $a\in \{1,2,...,m-1\}$, there exists a $b$ such that $ab\equiv 1(\mathrm{mod}m)$.

The reason composite $m$ don’t form fields is the presence of zero divisors. If $m$ is composite, then $m=ab$ for some integers $a$ and $b$, where $1<a,b<m$. This means $ab\equiv 0(\mathrm{mod}m)$, even though neither $a$ nor $b$ is congruent to 0 modulo $m$. In a field, the product of two non-zero elements must be non-zero.

When $m$ is prime, we denote the field as ${\mathbb{Z}}_p$ or $GF(p)$, where $p$ is the prime number. These are examples of Galois fields (also called finite fields).

However, Galois fields are more general than just ${\mathbb{Z}}_p$. For any prime $p$ and any positive integer $n$, there exists a unique (up to isomorphism) finite field with $p^n$ elements, denoted $GF(p^n)$.

When $n=1$, $GF(p)$ is indeed equivalent to ${\mathbb{Z}}_p$. However, for $n>1$, $GF(p^n)$ is not the same as ${\mathbb{Z}}_{p^n}$ (which is a ring but not a field when $n>1$). Constructing $GF(p^n)$ for $n>1$ requires more advanced techniques involving polynomials and modular arithmetic over polynomials, which we might discuss later.

Constructing Fields

Just as we can construct the finite field ${\mathbb{Z}}_p$ from the ring of integers $\mathbb{Z}$ by taking residues modulo a prime $p$, we can construct fields from polynomial rings. This process mirrors the progression from $\mathbb{Z}$ to ${\mathbb{Z}}_m$ (a ring) and further to ${\mathbb{Z}}_p$ (a field when $p$ is prime).

1. Starting with a Field: We begin with an existing field $F$ (e.g., ${\mathbb{Z}}_p$, $\mathbb{Q}$, $\mathbb{R}$, or $\mathbb{C}$).

2. Polynomial Ring: We construct the polynomial ring $F[x]$, which consists of all polynomials in the variable $x$ with coefficients in $F$. $F[x]$ is a Euclidean domain, meaning we have a notion of polynomial division with remainder, similar to integer division. This is crucial for the next steps.

3. Modulo an Irreducible Polynomial: Similar to modular arithmetic with integers, we introduce the concept of modular arithmetic with polynomials. We choose an irreducible polynomial $p(x)$ in $F[x]$. A polynomial is irreducible if it cannot be factored into a product of lower-degree polynomials in $F[x]$, analogous to prime numbers in integers.

4. The Quotient Ring: We form the quotient ring $F[x]/(p(x))$. This ring consists of the equivalence classes of polynomials in $F[x]$ modulo $p(x)$. Two polynomials are equivalent if they have the same remainder when divided by $p(x)$. The elements of the quotient ring can be represented by the polynomials of degree less than the degree of $p(x)$.

5. A Field: The crucial result is that if $p(x)$ is irreducible, then $F[x]/(p(x))$ is a field. This is analogous to ${\mathbb{Z}}_m$ being a field when $m$ is prime. The irreducibility of $p(x)$ ensures that every non-zero element in $F[x]/(p(x))$ has a multiplicative inverse. This quotient ring is also denoted $F[x{]}_{p(x)}$. This is an extension field of $F$.

Real Polynomial Rings $\mathbb{R}[x]$ and Galois Field Polynomials $GF(p)[x]$

Let’s consider the polynomial ring $\mathbb{R}[x]$, where polynomials have real coefficients.

• Reducible Polynomial: The polynomial $x^2+3x+2$ can be factored into $(x+1)(x+2)$ within $\mathbb{R}[x]$. Note that we can also deviate from the “canonical” factors to $(\pi x+\pi )\left(\frac{1}{\pi }x+\frac{2}{\pi }\right)$ and get infinite new “factors”.

• Irreducible Polynomial (in $\mathbb{R}[x]$): The polynomial $x^2+1$ cannot be factored into polynomials with real coefficients. Its roots are complex ($i$ and $-i$), so it is irreducible in $\mathbb{R}[x]$.

• Reducible Polynomial (in $\mathbb{R}[x]$): While $x^2+1$ is irreducible in $\mathbb{R}[x]$, $x^4+1$ can be factored within $\mathbb{R}[x]$ as $(x^2+\sqrt{2}x+1)(x^2-\sqrt{2}x+1)$. This factorization can be found by considering the complex roots of $x^4+1$ and multiplying conjugate pairs of roots to obtain quadratic factors with real coefficients.

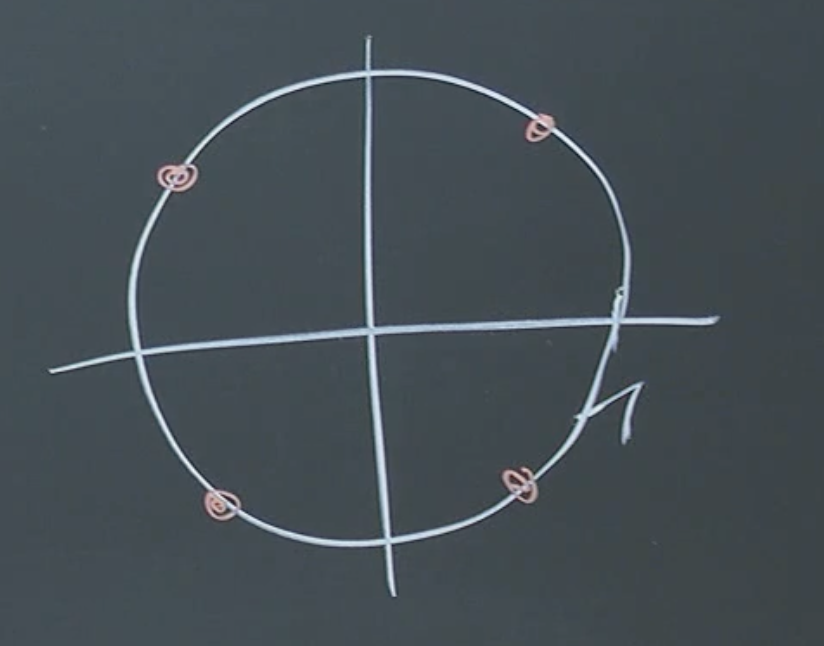
The key insight here is the Fundamental Theorem of Algebra.

Irreducible Polynomials in $\mathbb{R}[x]$

We’re exploring irreducible polynomials in $\mathbb{R}[x]$, the ring of polynomials with real coefficients. A polynomial is irreducible if it cannot be factored into lower-degree polynomials within the same ring. The key takeaway is that in $\mathbb{R}[x]$, the only irreducible polynomials are linear (degree 1) and certain quadratics (degree 2).

1. Fundamental Theorem of Algebra: The foundation of our understanding is the Fundamental Theorem of Algebra.

Fundamental Theorem of Algebra

Every non-constant polynomial with complex coefficients has at least one complex root.

This means even polynomials with real coefficients, when considered over the complex numbers, can be completely factored into linear factors.

2. Complex Conjugate Roots: A crucial consequence for real polynomials is the property of complex conjugate roots.

Complex Conjugate Roots

If a polynomial with real coefficients has a complex root $a+bi$ (where $b\ne 0$), then its complex conjugate $a-bi$ is also a root.

Proof: This stems from how complex conjugation interacts with arithmetic operations. Let $p(x)$ be a polynomial with real coefficients. If $z$ is a root, then $p(z)=0$. Since the coefficients are real, taking the conjugate of the whole equation gives $\overline{p(z)}=\overline{0}=0$. Due to the properties of conjugation, $\overline{p(z)}$ is the same as $p(\bar{z})$. Thus, $p(\bar{z})=0$, meaning $\bar{z}$ is also a root.

---

3. Constructing Real Quadratic Factors: This leads us to a powerful technique: pairing complex conjugate roots.

Constructing Real Quadratic Factors

If $a+bi$ and $a-bi$ are roots of a real polynomial, then multiplying the corresponding linear factors $(x-(a+bi))$ and $(x-(a-bi))$ gives: $(x-(a+bi))(x-(a-bi))=x^2-2ax+(a^2+b^2)$ This is a quadratic with real coefficients.

This shows that complex roots allow us to create irreducible quadratic factors in $\mathbb{R}[x]$.

4. Corollary: Factoring Real Polynomials: Combining these ideas gives us a powerful corollary.

Corollary for Real Polynomials

Every polynomial in $\mathbb{R}[x]$ of degree greater than 2 can be factored into a product of linear and quadratic factors with real coefficients.

This means higher-degree polynomials in $\mathbb{R}[x]$ are always reducible.

5. Examples:

• $x^2+1$: Irreducible in $\mathbb{R}[x]$ (complex roots $i$ and $-i$). Its discriminant is negative.
• $x^4+1$: Factors as $(x^2+\sqrt{2}x+1)(x^2-\sqrt{2}x+1)$ in $\mathbb{R}[x]$.
• $x^3-1$: Factors as $(x-1)(x^2+x+1)$ in $\mathbb{R}[x]$. The quadratic factor has a negative discriminant.

Conclusion:

In $\mathbb{R}[x]$, the only irreducible polynomials are linear polynomials and quadratic polynomials with negative discriminant. There are no irreducible polynomials of degree greater than 2 in $\mathbb{R}[x]$.

Greatest Common Divisors in $\mathbb{R}[x]$

Similar to integers, we can define the greatest common divisor (GCD) for polynomials in $\mathbb{R}[x]$.

Definition: The greatest common divisor of two polynomials $f(x)$ and $g(x)$ in $\mathbb{R}[x]$ is a polynomial $d(x)$ that satisfies:

1. Divisibility: $d(x)$ divides both $f(x)$ and $g(x)$. (Meaning $f(x)=d(x)q_1(x)$ and $g(x)=d(x)q_2(x)$ for some polynomials $q_1(x)$ and $q_2(x)$ in $\mathbb{R}[x]$).
2. Greatest: If any other polynomial $c(x)$ divides both $f(x)$ and $g(x)$, then $c(x)$ must also divide $d(x)$.

Uniqueness: The GCD is not unique in the strictest sense. If $d(x)$ is a GCD, then any non-zero constant multiple of $d(x)$ (e.g., $2d(x)$, $-d(x)$, $\frac{1}{3}d(x)$) is also a GCD. To address this, we often choose the monic polynomial among the GCDs, which is the polynomial with a leading coefficient of 1. This makes the GCD unique.

Example:

Find the GCD of $f(x)=x^2+4x+3$ and $g(x)=x^2+3x+2$.

1. Factorization: We factor both polynomials: $f(x)=(x+1)(x+3)$ $g(x)=(x+1)(x+2)$

2. Common Factors: The only common factor is $(x+1)$.

3. GCD: Therefore, the GCD of $f(x)$ and $g(x)$ is $x+1$. Note that any constant multiple of $(x+1)$, such as $2x+2$ or $-x-1$, would also technically be a GCD, but $x+1$ is the monic GCD.

Computing the GCD:

Just as with integers, we can use the Euclidean algorithm to compute the GCD of two polynomials without necessarily factoring them. The Euclidean algorithm involves repeated polynomial division until the remainder is zero. The last non-zero remainder is the GCD.

Note about “positive”:

The concept of “positive” doesn’t directly apply to polynomials in the same way it does to integers. Instead, we use the convention of choosing the monic polynomial for the GCD to ensure uniqueness.

Examples

Example: Factoring in $GF(5)[x]$

We’re working within $GF(5)[x]$, which is the same as ${\mathbb{Z}}_5[x]$, the ring of polynomials with coefficients in the finite field ${\mathbb{Z}}_5$. Since 5 is prime, ${\mathbb{Z}}_5$ is indeed a field.

Consider the polynomial $f(x)=x^3+4x^2+1$. We want to determine if it’s factorable in $GF(5)[x]$.

Checking for Roots:

A straightforward way to check for factorability is to test if $f(x)$ has any roots in ${\mathbb{Z}}_5$. If $f(a)=0$ for some $a\in {\mathbb{Z}}_5$, then $(x-a)$ is a factor. Remember that in ${\mathbb{Z}}_5$, the elements are $\{0,1,2,3,4\}$.

• $f(0)=0^3+4(0^2)+1=1\not\equiv 0(\mathrm{mod}5)$
• $f(1)=1^3+4(1^2)+1=6\equiv 1\not\equiv 0(\mathrm{mod}5)$
• $f(2)=2^3+4(2^2)+1=8+16+1=25\equiv 0(\mathrm{mod}5)$

We’ve found a root! Since $f(2)=0$, $(x-2)$ is a factor. In $GF(5)$, $-2\equiv 3(\mathrm{mod}5)$, so we can write the factor as $(x+3)$.

Polynomial Division:

Now we perform polynomial division to find the other factor. We divide $x^3+4x^2+1$ by $(x+3)$ in ${\mathbb{Z}}_5[x]$:

x^2 + x + 2
__________________________
x+3 | x^3 + 4x^2 + 0x + 1
    -(x^3 + 3x^2)
    __________________________
           x^2 + 0x + 1
         -(x^2 + 3x)
    __________________________
              -3x + 1
            -(-3x - 9) // since -3 mod 5 = 2 mod 5 
    __________________________
                   10
                   10 mod 5 = 0. // we calculate in modulo 5

So, $x^3+4x^2+1=(x+3)(x^2+x+2)$ in $GF(5)[x]$.

Now if we try to see if we can factor $x^2+x+2$, you’ll notice we can’t. This can be done by manually trying all values $0{\dots }_4$.

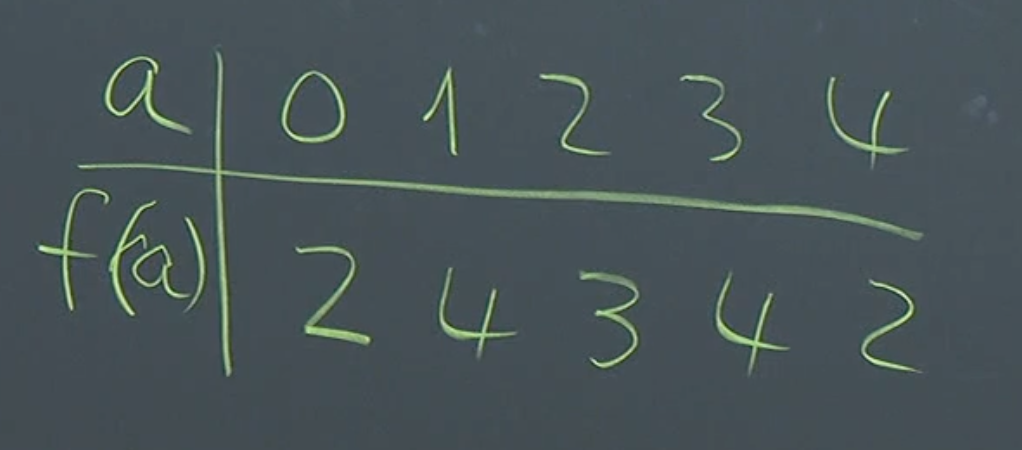
Further Factorization:

Now we need to check if $x^2+x+2$ is further factorable in $GF(5)[x]$. We can test for roots again:

• $f(0)=2$
• $f(1)=4$
• $f(2)=2+2+2=1$
• $f(3)=4+3+2=4$
• $f(4)=1+4+2=2$

Since $x^2+x+2$ has no roots in $GF(5)$, it is irreducible in $GF(5)[x]$.

Therefore, the complete factorization of $x^3+4x^2+1$ in $GF(5)[x]$ is $(x+3)(x^2+x+2)$.

Example: Factoring in $GF(2)[x]$

Consider the polynomial $x^5+x^4+1$ in $GF(2)[x]$. We want to factor this polynomial.

Testing for Roots:

First, we check for roots in $GF(2)=\{0,1\}$:

• For $x=0$: $0^5+0^4+1=1\ne 0$
• For $x=1$: $1^5+1^4+1=1+1+1=3\equiv 1\ne 0(\mathrm{mod}2)$

Since there are no roots in $GF(2)$, the polynomial has no linear factors. We must look for higher-degree factors.

Factoring using Irreducible Polynomials:

One approach is to try dividing by irreducible polynomials of degree 2 and 3. In $GF(2)[x]$, the only irreducible polynomial of degree 2 is $x^2+x+1$. Let’s try dividing $x^5+x^4+1$ by $x^2+x+1$:

x^3 + x + 1
____________________________
x^2+x+1 | x^5 + x^4 + 0x^3 + 0x^2 + 0x + 1
         -(x^5 + x^4 + x^3)
         ____________________________
                 -x^3 + 0x^2 + 0x + 1
                 -(-x^3 - x^2 - x)
         ____________________________
                       x^2 + x + 1
                     -(x^2 + x + 1)
         ____________________________
                            0

So $x^5+x^4+1=(x^2+x+1)(x^3+x+1)$ and it divides without any reminder. Now we know that $x^2+x+1$ is already irreducible since there are no roots for this polynom, so we look at $x^3+x+1$:

• $x=0$: $1$
• $x=1$: $1$

So $x^3+x+1$ is also an irreducible polynom since there are no roots.

As a side remark, there exist efficient algorithms to do this kind of factorization.

Example: Dividing with Residue in $GF(7)[x]$

We want to divide $3x^4+x+5$ by $2x^2+x+1$ in $GF(7)[x]$. This means all coefficients are considered modulo 7.

Here’s the division worked out step-by-step, keeping in mind that we’re working modulo 7:

1. First term: We want to multiply $2x^2+x+1$ by something to match the leading term $3x^4$. We need $2x^2\cdot ?=3x^4$. Since $2\cdot 5\equiv 3(\mathrm{mod}7)$ then $2\cdot 5x^2=3x^4$. Since $2^{-1}\equiv 4(\mathrm{mod}7)$ then $5=3/2=3\cdot 4=12\equiv 5(\mathrm{mod}7)$. So, we multiply by $5x^2$:

   $5x^2(2x^2+x+1)=3x^4+5x^3+5x^2\equiv 3x^4+5x^3+5x^2(\mathrm{mod}7)$

   Subtracting this from $3x^4+x+5$ gives $2x^3+2x^2+x+5$. ($-5\equiv 2(\mathrm{mod}7)$)

2. Second Term: Now we want $2x^2\cdot ?=2x^3$. We multiply by $x$:

   $x(2x^2+x+1)=2x^3+x^2+x$

   Subtracting this gives $x^2+5$.

3. Third Term: We want $2x^2\cdot ?=x^2$. We multiply by $4$: $4(2x^2+x+1)=x^2+4x+4$ Then we have $x^2+5-(x^2+4x+4)=-4x+1=3x+1$.

Since the degree of the remainder $3x+1$ is less than the degree of the divisor $2x^2+x+1$, we stop here.

Result:

The quotient is $5x^2+x+4$, and the remainder is $3x+1$.

Therefore, $3x^4+x+5=(2x^2+x+1)(5x^2+x+4)+(3x+1)$ in $GF(7)[x]$.

Similar Example in $GF(2)[x]$

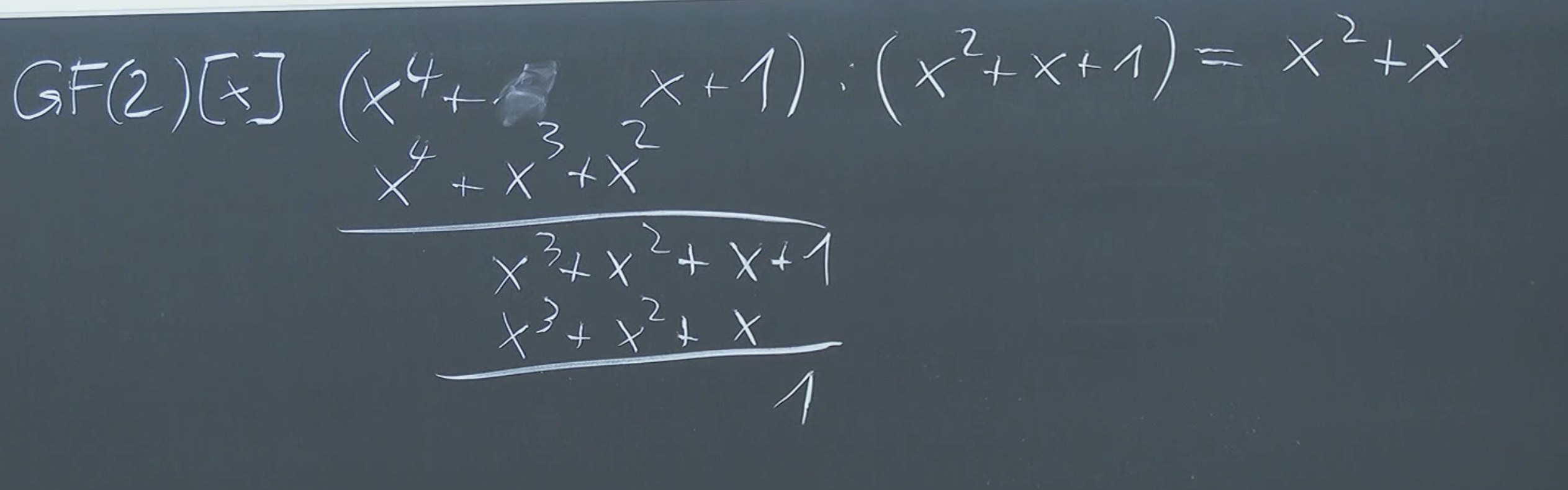
The Division Algorithm and GCD for Polynomials

A fundamental result for polynomials is the division algorithm, which allows us to divide one polynomial by another and obtain a unique quotient and remainder.

Theorem (Division Algorithm for Polynomials): Given two polynomials $a(x)$ and $b(x)$ in $F[x]$ (where $F$ is a field and $b(x)\ne 0$), there exist unique polynomials $q(x)$ (the quotient) and $r(x)$ (the remainder) in $F[x]$ such that:

$a(x)=b(x)q(x)+r(x)$

where either $r(x)=0$ or $\text{deg}(r(x))<\text{deg}(b(x))$.

Note: The condition on the degree of the remainder is crucial. It ensures that the remainder is “smaller” than the divisor, making the division process terminate.

GCD and the Euclidean Algorithm:

The division algorithm is the basis for the Euclidean algorithm, which computes the GCD of two polynomials.

Euclidean Algorithm:

1. Given two polynomials $a(x)$ and $b(x)$, assume without loss of generality that $\text{deg}(a(x))\ge \text{deg}(b(x))$.
2. Divide $a(x)$ by $b(x)$: $a(x)=b(x)q_1(x)+r_1(x)$, where $\text{deg}(r_1(x))<\text{deg}(b(x))$.
3. If $r_1(x)=0$, then $b(x)$ is the GCD.
4. Otherwise, replace $a(x)$ with $b(x)$ and $b(x)$ with $r_1(x)$, and repeat the division: $b(x)=r_1(x)q_2(x)+r_2(x)$, where $\text{deg}(r_2(x))<\text{deg}(r_1(x))$.
5. Continue this process until the remainder is zero. The last non-zero remainder is the GCD of $a(x)$ and $b(x)$.

Example:

Find the GCD of $a(x)=x^3+2x^2+x+2$ and $b(x)=x^2+1$ in $\mathbb{R}[x]$.

1. $x^3+2x^2+x+2=(x^2+1)(x+2)+0$

Since the remainder is 0 in the first step, the GCD is $x^2+1$.

Uniqueness: As mentioned before, the GCD is unique up to a constant multiple. We typically choose the monic polynomial as the GCD. In the example above, $x^2+1$ is already monic.

Continue here: 19 Factorizations, Polynomial Fields and Division, Polynomial Interpolation, Constructing Galois Fields