20 Pseudoinverses, Constructing Pseudoinverses

Lecture from 22.11.2024 | Video: Videos ETHZ

The Pseudoinverse

The pseudoinverse, also called the Moore-Penrose Inverse and denoted as $A^{†}$, generalizes the matrix inverse for matrices that are not invertible. This includes matrices that are non-square or singular.

Challenges with Inverses

For certain systems, such as $A\mathbf{x}=\mathbf{b}$, there can be multiple complications:

• The system may have no solution.
• The system may have infinitely many solutions.
• We need an operation that generalizes the matrix inverse to handle such cases, ideally represented as a matrix multiplication.

Plan for Defining the Pseudoinverse

1. For full column rank matrices, we define the pseudoinverse.
2. For full row rank matrices, we provide a different definition.
3. For general matrices, we extend the pseudoinverse definition.

Pseudoinverse for Full Column Rank Matrices

Let’s delve into the concept of the pseudoinverse, a powerful tool in linear algebra that allows us to handle systems of equations, especially overdetermined ones, where we have more equations than unknowns. Think of trying to fit a line to a cloud of data points—there’s likely no single line that goes through all the points, leading to an overdetermined system.

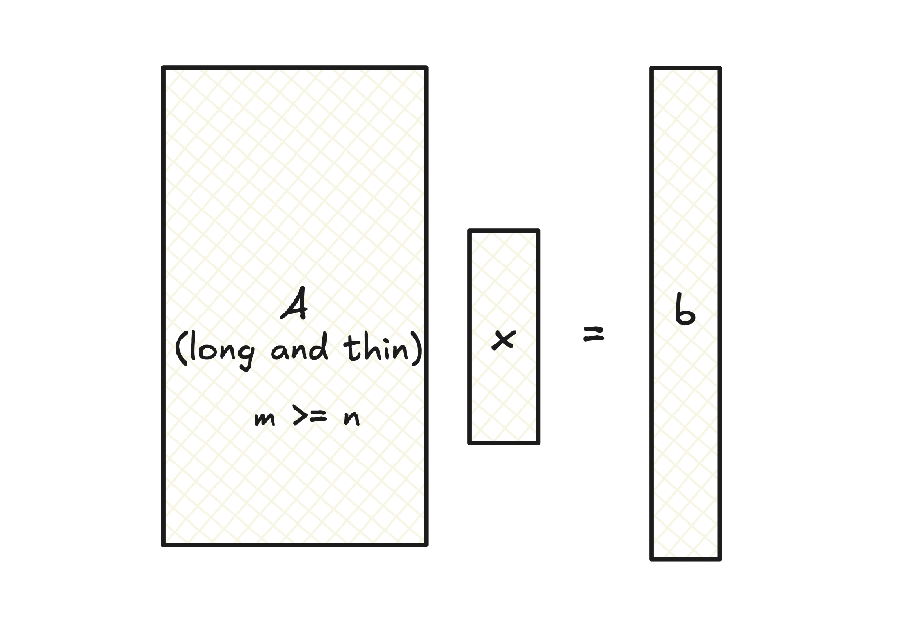
When dealing with a matrix $A$ that has full column rank (meaning its columns are linearly independent), we can define a special kind of inverse called the pseudoinverse. This comes in handy when we can’t find a true inverse (e.g., when $A$ is not square) but still want to solve equations involving $A$.

Definition

For an $m\times n$ matrix $A$ with full column rank (rank($A$) = $n$), the pseudoinverse $A^{†}$ is defined as:

$A^{†}=(A^{T}A{)}^{-1}{A}^T$

Notice that $A^{T}A$ is a square $n\times n$ matrix, and since $A$ has full column rank, $A^{T}A$ is invertible. This invertibility is crucial for the existence of the pseudoinverse.

Proposition

The pseudoinverse $A^{†}$ acts as a left inverse for $A$:

$A^{†}A=I$

Proof

The proof is straightforward. Since we’ve established that $A^{T}A$ is invertible, we can simply substitute the definition of $A^{†}$:

$A^{†}A=(A^{T}A{)}^{-1}{A}^{T}A=I$

Example

Let’s solidify this with a concrete example. Take the matrix:

$A=\left[\begin{array}{c}1\\ 2\end{array}\right]$

1. Compute $A^{T}A$: $A^{T}A=\left[\begin{array}{cc}1& 2\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right]=5$

2. Compute the pseudoinverse: $A^{†}=\frac{1}{5}\left[\begin{array}{cc}1& 2\end{array}\right]$

3. Verify the left inverse property: $A^{†}A=\frac{1}{5}\left[\begin{array}{cc}1& 2\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right]=\frac{1}{5}(5)=1$

Least Squares Solution and Projection

Now, let’s connect the pseudoinverse to the problem of solving $A\mathbf{x}=\mathbf{b}$, especially when it’s overdetermined. Because $A$ has full column rank, we likely won’t find an exact solution. However, we can seek the next best thing: a least squares solution, minimizing the squared error $\Vert \mathbf{b}-A\mathbf{x}{\Vert }^2$.

We want to project $\mathbf{b}$ into $C(A)$. The projection is given by $A\hat{x}$ for some vector $\hat{x}$. The error $\mathbf{b}-A\hat{x}$ must be orthogonal to $C(A)$. Since $C(A^T)=C(A{)}^{\perp }$, the error must be in $C(A^T)$, i.e. it must be orthogonal to the column space of $A$. This is expressed by $A^T(\mathbf{b}-A\hat{\mathbf{x}})=0$, leading to the normal equation:

$A^{T}A\hat{\mathbf{x}}=A^T\mathbf{b}$

We know $A^{T}A$ is invertible since $A$ has full column rank, so we can solve for $\hat{\mathbf{x}}$:

$\hat{\mathbf{x}}=(A^{T}A{)}^{-1}{A}^T\mathbf{b}$

Look closely—this is exactly $A^{†}\mathbf{b}$! So, the pseudoinverse gives us a direct way to compute the least squares solution:

$\hat{\mathbf{x}}=A^{†}\mathbf{b}$

The pseudoinverse efficiently handles the projection step implicit in the least squares solution, finding the vector $\mathbf{x}$ that minimizes the error $\Vert \mathbf{b}-A\mathbf{x}{\Vert }^2$. In essence, $A\hat{\mathbf{x}}$ is the projection of $\mathbf{b}$ onto the column space of $A$, which is the closest we can get to solving $A\mathbf{x}=\mathbf{b}$ in an overdetermined system.

Pseudoinverse for Full Row Rank Matrices

Now, let’s explore the pseudoinverse for matrices with full row rank. This scenario arises when you have more unknowns than equations – an underdetermined system. Imagine having two equations but three unknowns ; there are infinitely many solutions, right? The pseudoinverse helps us find a specific solution among these: the one with the smallest norm (length).

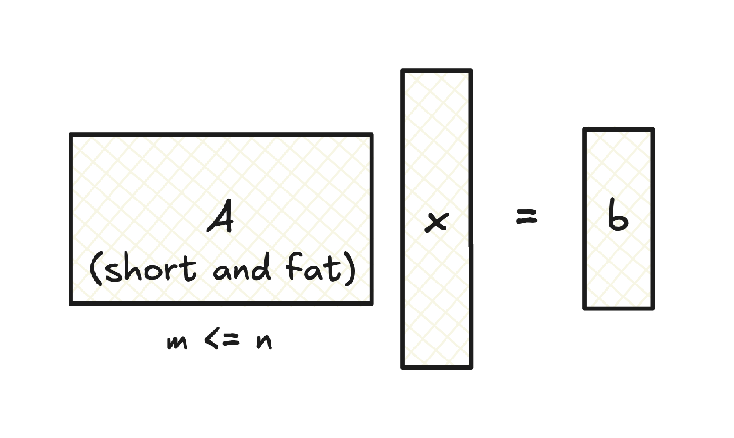
Definition

For an $m\times n$ matrix $A$ with full row rank (rank($A$) = $m$), the pseudoinverse is defined as:

$A^{†}=A^T(A{A}^T{)}^{-1}$

In this case, $A{A}^T$ is a square $m\times m$ matrix, and since $A$ has full row rank, $A{A}^T$ is invertible. This, again, is essential for the pseudoinverse to exist.

Alternative Derivation of the Pseudoinverse for Full Row Rank

Let’s add another perspective on deriving the pseudoinverse for full row rank matrices. We can cleverly leverage what we already know about the pseudoinverse for full column rank matrices.

Recall that if a matrix has full row rank, its transpose has full column rank. So, if $A$ is $m\times n$ with full row rank ($rank(A)=m$), then $A^T$ is $n\times m$ with full column rank ($rank(A^T)=m$).

We already know how to compute the pseudoinverse of a full column rank matrix. So, we can find the pseudoinverse of $A^T$:

$(A^T{)}^{†}=((A^T{)}^T{A}^T{)}^{-1}(A^T{)}^T=(A{A}^T{)}^{-1}A$

Now, remember a key property we’ll prove later about pseudoinverses: $(A^T{)}^{†}=(A^{†}{)}^T$. This means that the pseudoinverse of the transpose is equal to the transpose of the pseudoinverse.

Using this property, we can find $A^{†}$ by simply taking the transpose of $(A^T{)}^{†}$:

$A^{†}=((A^T{)}^{†}{)}^T=((A{A}^T{)}^{-1}A{)}^T=A^T(A{A}^T{)}^{-1}$

And there we have it! This is precisely the definition of the pseudoinverse for a full row rank matrix. This alternative derivation neatly demonstrates a connection between the full row rank and full column rank cases. It showcases how understanding one case can illuminate others through the use of transposes and their properties.

Proposition

The pseudoinverse $A^{†}$ acts as a right inverse for $A$:

$A{A}^{†}=I$

Proof

Similar to the full column rank case, the proof is a simple substitution:

$A{A}^{†}=A{A}^T(A{A}^T{)}^{-1}=I$

Example

Let’s illustrate this with an example. Consider the matrix:

$A=\left[\begin{array}{cc}1& 2\end{array}\right]$

1. Compute $A{A}^T$: $A{A}^T=\left[\begin{array}{cc}1& 2\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right]=5$

2. Compute the pseudoinverse: $A^{†}=\left[\begin{array}{c}1\\ 2\end{array}\right]\frac{1}{5}=\left[\begin{array}{c}1/5\\ 2/5\end{array}\right]$

3. Verify the right inverse property: $A{A}^{†}=\left[\begin{array}{cc}1& 2\end{array}\right]\left[\begin{array}{c}1/5\\ 2/5\end{array}\right]=\frac{1}{5}+\frac{4}{5}=1$

Minimum-Norm Solution and its Relevance

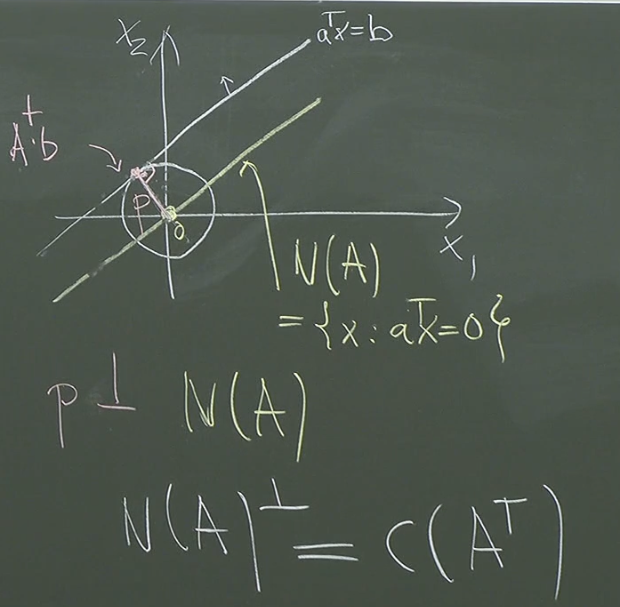
The pseudoinverse is particularly useful when $A\mathbf{x}=\mathbf{b}$ has infinitely many solutions (e.g., when $A$ has full row rank and $n>m$). In such cases, it pinpoints the unique solution with the smallest magnitude (the minimum Euclidean norm).

Importance of Minimum-Norm Solutions:

• Efficiency (Engineering): Often corresponds to the least resource-intensive solution.
• Simplicity (Machine Learning, etc.): Represents the simplest explanation among equivalent solutions.
• Stability: More resilient to noise or errors.

Proof of Minimum-Norm Property

Our goal is to prove that $\hat{\mathbf{x}}=A^{†}\mathbf{b}$ is the minimum-norm solution among all solutions to $A\mathbf{x}=\mathbf{b}$ when $A$ has full row rank.

1. General Solution

Any solution to $A\mathbf{x}=\mathbf{b}$ can be expressed as:

where $\mathbf{w}$ is an arbitrary vector.

• Particular Solution: $A^{†}\mathbf{b}$ is a particular solution because, for full row rank matrices, $A{A}^{†}=I$. Therefore:

• Nullspace Component: $(I-A^{†}A)\mathbf{w}$ lies in the nullspace of $A$. This is because:

Thus, adding any multiple of a nullspace vector to a particular solution yields another solution.

2. Orthogonality

The key insight is that:

• $A^{†}\mathbf{b}$ lies in the row space of $A$ (denoted $C(A^T)$).
• $(I-A^{†}A)\mathbf{w}$ lies in the nullspace of $A$.

The row space and nullspace are orthogonal complements. This orthogonality is crucial for the next step.

3. Pythagorean Theorem and Minimum Norm

The norm squared of any solution $\mathbf{x}$ can be written as:

Using the Pythagorean theorem (since the components are orthogonal):

To minimize $\Vert \mathbf{x}{\Vert }^2$, we must minimize the second term $\Vert (I-A^{†}A)\mathbf{w}{\Vert }^2$.

4. Nullspace Component Minimization

The term $\Vert (I-A^{†}A)\mathbf{w}{\Vert }^2$ is minimized when $\mathbf{w}$ lies entirely in the row space of $A$, making $(I-A^{†}A)\mathbf{w}=0$. In this case, the solution simplifies to:

5. The Pseudoinverse Solution

Thus, the pseudoinverse provides the solution with the minimum norm because it eliminates the nullspace component, leaving the solution entirely within the row space of $A$.

Pseudoinverse for General Matrices

CR Decomposition

Any $m\times n$ matrix $A$ with rank($A$) = $r$ can be factored as:

where:

• $C$ is an $m\times r$ matrix with full column rank (formed by the first $r$ linearly independent columns of $A$), and
• $R$ is an $r\times n$ matrix with full row rank (formed by the coefficients of $A$ in the basis of its column space).

Definition of Pseudoinverse for General Matrices

For a matrix $A$ with rank $r$ and CR decomposition $A=CR$, the pseudoinverse $A^{†}$ is defined as:

Alternatively, this can be expressed as:

Lemma (Minimum-Norm Least Squares Solution)

For $A\in {\mathbb{R}}^{m\times n}$ and $\mathbf{b}\in {\mathbb{R}}^m$, the unique solution to:

is given by:

This result gives the minimum-norm least squares solution.

Proof of Minimum-Norm Least Squares Solution (General Case and Lemma)

This proof addresses both the minimum-norm solution for full row rank matrices and the general lemma concerning the minimum-norm least squares solution using the CR decomposition.

1. The Goal

We aim to prove that for any $A\in {\mathbb{R}}^{m\times n}$ and $\mathbf{b}\in {\mathbb{R}}^m$, the unique solution to:

is given by $\hat{\mathbf{x}}=A^{†}\mathbf{b}$. This handles underdetermined (full row rank), overdetermined (full column rank), and general cases.

2. CR Decomposition and Pseudoinverse

Let rank($A$) = $r$. Decompose $A=CR$, where:

• $C\in {\mathbb{R}}^{m\times r}$ has full column rank (captures the first $r$ linearly independent columns of $A$),
• $R\in {\mathbb{R}}^{r\times n}$ has full row rank (maps the row space).

The pseudoinverse of $A$ is given by $A^{†}=R^{†}{C}^{†}$, where:

• $C^{†}=(C^{T}C{)}^{-1}{C}^T$ and $R^{†}=R^T(R{R}^T{)}^{-1}$.

3. Rewriting the Normal Equations

The constraint $A^{T}A\mathbf{x}=A^T\mathbf{b}$ is equivalent to solving the least squares problem. Substituting $A=CR$ into the equations gives:

This simplifies to:

Because $R$ has full row rank, $R^T$ has full column rank, meaning $N(R^T)=\{0\}$. Thus, we can reduce this to:

4. Expressing the General Solution

Since $C$ has full column rank, $C^{T}C$ is invertible. Therefore, we solve:

To find the minimum-norm solution, we consider the general solution form for $R$ (from earlier proofs):

where $\mathbf{w}$ is an arbitrary vector, and $R^{†}=R^T(R{R}^T{)}^{-1}$. The minimum-norm solution occurs when the nullspace component vanishes:

Substituting $R^{†}$ and $C^{†}$:

This is equivalent to $A^{†}\mathbf{b}$. Thus, $\hat{\mathbf{x}}=A^{†}\mathbf{b}$ is the minimum-norm solution.

5. Connecting to the Full Row Rank Case

When $A$ has full row rank ($r=m$), $C$ becomes an invertible $m\times m$ matrix. In this case:

• The pseudoinverse simplifies to $A^{†}=A^T(A{A}^T{)}^{-1}$, consistent with earlier definitions.
• The proof proceeds similarly since $C$ is invertible, allowing $R=C^{-1}A$. This leads to:

Solving, we find:

Following the same steps, we deduce the minimum-norm solution as:

This confirms that $A^{†}=A^T(A{A}^T{)}^{-1}$ yields the same minimum-norm solution.

Summary

This proof uses the CR decomposition and properties of full rank matrices to establish the general minimum-norm least squares solution. It connects to the specific case of full row rank matrices, showing how the pseudoinverse unifies all cases. The solution:

minimizes the error in the least-squares sense while also ensuring the smallest possible norm, addressing both accuracy and efficiency.

Properties of the Pseudoinverse

Theorem

For any matrix $A\in {\mathbb{R}}^{m\times n}$, the following properties hold:

1. $A{A}^{†}A=A$ and $A^{†}A{A}^{†}=A^{†}$.
2. $A{A}^{†}$ is symmetric and is the projection matrix onto the column space $C(A)$.
3. $A^{†}A$ is symmetric and is the projection matrix onto the row space $C(A^T)$.
4. $(A^T{)}^{†}=(A^{†}{)}^T$.

Proof of Properties

1. $A{A}^{†}A=A$ and $A^{†}A{A}^{†}=A^{†}$:

   Using the CR decomposition $A=CR$, we already know $A{A}^{†}A=A$. Now, for $A^{†}A{A}^{†}$:

   $$A^{†}A{A}^{†}=R^{†}{C}^{†}CR{R}^{†}{C}^{†}=R^{†}R{R}^{†}{C}^{†}=R^{†}{C}^{†}=A^{†},$$

   since $R{R}^{†}=I$ (for full row rank) and $C^{†}C=I$ (for full column rank).

2. $A{A}^{†}$ Projects Onto $C(A)$:

   Using the CR decomposition:

   $$A{A}^{†}=CR{R}^{†}{C}^{†}=C{C}^{†}.$$

   Since $C^{†}C=I$, $C{C}^{†}$ is the projection onto $C(A)$. It is symmetric because the pseudoinverse ensures $C{C}^{†}=(C{C}^{†}{)}^T$.

3. $A^{†}A$ Projects Onto $C(A^T)$:

   Similarly, using the CR decomposition:

   $$A^{†}A=R^{†}{C}^{†}CR=R^{†}R.$$

   This is symmetric and projects onto $C(A^T)$, as $R^{†}R$ spans the row space of $A$.

4. $(A^T{)}^{†}=(A^{†}{)}^T$:

   For full column rank, $(A^T{)}^{†}=(A{A}^T{)}^{-1}A=(A(A^{T}A{)}^{-1}{A}^T{)}^T=(A^{†}{)}^T$.

   For full row rank, $(A^T{)}^{†}=((A^T{)}^T(A^T(A^T{)}^T{)}^{-1})=A(A^{T}A{)}^{-1}=(A^T(A{A}^T{)}^{-1}{)}^T=(A^{†}{)}^T$.

   For general $A=CR$, we have:

   $$(A^T{)}^{†}=(R^T{C}^T{)}^{†}=C(C^{T}C{)}^{-1}(R{R}^T{)}^{-1}R=((R^{†}{)}^T(C^{†}{)}^T{)}^T=(C^{†}{R}^{†}{)}^T=(A^{†}{)}^T.$$

This completes the proof of the properties of the pseudoinverse.

Continue here: 21 Certificates, Linear Systems of Inequalities, Projections of Polyhedra, Farkas Lemma