21 Logic, Proof Systems, Logical Consequence, Syntactic Derivation

Lecture from: 27.11.2024 | Video: Videos ETHZ

Logic: Formalizing Proofs and Verification

In computer science, rigorous proofs are often necessary, especially in areas like cryptography, program verification, and distributed systems. Logic provides the tools for constructing and evaluating these proofs. This chapter explores proof systems, logical sequences, and the nature of proofs, laying the groundwork for applications in various computer science domains.

Proof Systems: A Formal Model

A proof system consists of three key components:

1. Statement ($S$): The assertion we want to prove.
2. Proof ($P$): The evidence or argument supporting the statement.
3. Verification Function ($\varphi$): A function that checks the validity of a purported proof for a given statement: $\varphi (S,P)\in \{0,1\}$ (0 for reject, 1 for accept).

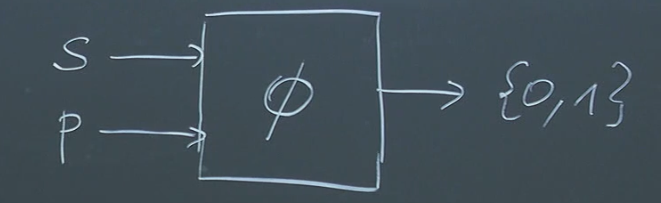
This model formalizes the notion of a proof. The specific representations of statements, proofs, and the verification function can vary, but the core structure remains the same.

Beyond Static Proofs

While we primarily focus on static proofs, where $P$ is presented completely, other models exist:

Interactive Proofs and Zero-Knowledge Proofs

• Interactive Proofs: A prover and a verifier engage in a dialogue, with the verifier asking questions and the prover providing answers. This interaction allows for more complex proof scenarios.
• Zero-Knowledge Proofs: A special case of interactive proofs where the prover convinces the verifier of a statement’s truth without revealing any information beyond the statement’s validity. These are crucial in cryptography and blockchain technologies.

Formalizing Statements, Proofs, and Semantics

To build a rigorous system, we need to formalize the components:

1. Statements ($\mathcal{S}$): $\mathcal{S}$ represents the set of all possible statements. We can represent statements as strings over an alphabet $\Sigma$. Without loss of generality, we can use a binary alphabet $\Sigma =\{0,1\}$, so $\mathcal{S}=\{0,1{\}}^{\ast }$, the set of all binary strings. The syntax of a language defines which strings in $\mathcal{S}$ are well-formed statements.

2. Proofs ($\mathcal{P}$): Similar to statements, proofs can be represented as strings: $\mathcal{P}=\{0,1{\}}^{\ast }$. The structure of valid proofs depends on the specific proof system.

3. Semantics ($\tau$): Semantics assigns meaning to statements. It’s a function $\tau :\mathcal{S}\to \{0,1\}$ that determines the truth value of a statement (0 for false, 1 for true). The semantics incorporates the rules and interpretations necessary to evaluate the truth of a statement.

Example: Sudoku

Consider a Sudoku puzzle:

1. Statement and Semantics

• Statement ($S$): A Sudoku puzzle can be represented as a string. For example, using ‘x’ for empty cells, a Sudoku board could be represented by an 81-character string like xx7x1x.... If we represent each of the 9 digits and ‘x’ with 4 bits, this string becomes a $81\cdot 4=324$-bit string.
• Semantics ($\tau$): The semantics $\tau :S\to \{0,1\}$ determines whether the Sudoku puzzle represented by the string $S$ has a solution. $\tau (S)=1$ if a solution exists, and 0 otherwise. $\tau$ encapsulates the rules of Sudoku.

2. Proof and Verification

• Proof of Solvability ($P$): A proof of solvability could be a string representing a valid solution to the Sudoku puzzle. This would also be an 81-character string of digits 1 through 9, without ‘x’.
• Verification Function ($\varphi$): The verification function $\varphi (S,P)$ checks two things: (1) whether the digits in $P$ are consistent with the initially filled cells in $S$, and (2) whether $P$ represents a valid Sudoku solution (rows, columns, and blocks contain distinct digits).

3. Proof of Unsolvability

Proving unsolvability is more challenging.

• Statement ($S$): The same as before – the string representation of the Sudoku puzzle.
• Semantics ($\tau$): Now, $\tau (S)=1$ if the puzzle has no solution, and 0 otherwise.
• Proof ($P$): A proof of unsolvability might demonstrate a contradiction. For example if every possible solution leads to a violation of a sudoku rule (like having two identical digits in the same row, colum or $3\times 3$ square).

• Verification Function ($\varphi$): The verification function would need to check the logic of the contradiction presented in $P$.

4. The Challenge of a General Proof System

While we can construct proofs for specific Sudoku instances, designing a general, efficient verification function $\varphi$ that works for all Sudoku puzzles (and all possible proofs of solvability or unsolvability) is difficult. Whether a computationally feasible such function exists is still open. This is linked to the $P$ versus $NP$ problem.

A brute-force approach, trying all possible combinations of digits, could determine solvability, but it’s computationally expensive. The same applies to other problems, like primality testing.

Brute-Force vs. Efficient Verification

Brute-Force Approaches

• Sudoku: A brute-force algorithm could try all possible digit combinations until a valid solution is found or all possibilities are exhausted. This proves solvability or unsolvability, but the time complexity is enormous.
• Primality Testing: To verify if a number $p$ is prime, a naive approach checks for divisibility by all integers from 2 up to $\sqrt{p}$. This is more efficient than checking all the way up to $p-1$, but still computationally expensive for very large numbers. Moreover, providing the prime factorization of $p$ proves compositeness quite easily, thus verifying is easy, finding it is hard.

The Purpose of a Proof ($P$)

The key idea behind a proof system is that the verification function $\varphi (S,P)$ should be significantly more efficient than determining the truth of $S$ directly. If $\varphi$ could determine the truth of $S$ on its own (e.g., by brute force), the need for a separate proof $P$ would diminish. The purpose of $P$ is to provide a shortcut, allowing for efficient verification without the need for computationally intensive calculations.

The Challenge of Efficient Proof Systems

For some problems, like Sudoku and primality testing, it’s not immediately clear whether efficient, non-brute-force proof systems exist. This is a fundamental question in computational complexity theory.

Primality Testing: A Breakthrough with "PRIMES is in P"

For primality testing, finding an efficient proof system (without brute-force or probabilistic methods) was a long-standing open question. A significant breakthrough came in 2002 with the Agrawal–Kayal–Saxena (AKS) primality test, published in their 2004 paper “PRIMES is in P.” This paper introduced a deterministic, polynomial-time algorithm to determine if a number is prime.

This result means there exists an efficient verification function $\varphi$ for primality. Before AKS, it wasn’t clear whether a deterministic polynomial-time primality testing algorithm existed at all, thus the question about the existence of a primality proof system was unresolved too. The AKS algorithm itself doesn’t require an explicit proof certificate $P$ to be given. Instead, you could interpret it in two ways: either by assuming $P$ is an empty input or, alternatively, viewing components of the AKS algorithm as an implicit certificate that the function $\varphi$ then validates. It is not a proof system but a primality checking algorithm. Thus the input $P$ is not needed.

This highlights the distinction between finding an efficient algorithm to decide a property (like primality) and having a traditional proof system where a separate, easily verifiable proof $P$ must be explicitly provided. The AKS algorithm blurs this distinction somewhat, as it provides a method for efficiently deciding primality without the need for a separate, explicitly provided proof. Thus, the algorithm itself acts as both the “proof” and the “verification” in one combined process.

Requirements for a Sound and Complete Proof System

A robust proof system should possess two fundamental properties: soundness and completeness. These properties guarantee that the proof system accurately reflects the truth of statements within its framework. We want our verification function, $\varphi$, to adhere to these properties.

1. Soundness

Soundness ensures that the proof system only accepts valid proofs, preventing the “proof” of false statements.

Soundness

For all statements $S\in \mathcal{S}$ and proofs $P\in \mathcal{P}$, if $\varphi (S,P)=1$ (the proof is accepted), then $\tau (S)=1$ (the statement is true).

In essence, if a proof is accepted, the statement it supposedly proves must be true. No false positives are allowed.

• Contrapositive: A useful equivalent formulation is the contrapositive: If $\tau (S)=0$ (the statement is false), then $\varphi (S,P)=0$ for all $P$ (no proof can be accepted).

• Why Not Predicate Logic to Define Soundness?: While we could express soundness using predicate logic (e.g., $\forall S\in \mathcal{S}(\exists P\in \mathcal{P}(\varphi (S,P)=1)\to \tau (S)=1)$), this is not ideal. We want to use logic to define soundness, not the other way around. A direct definition avoids circularity.

• No Backward Implication: Soundness does not guarantee that every true statement has a proof. It only ensures that accepted proofs correspond to true statements. A system can be sound but unable to prove all true statements.

2. Completeness

Completeness ensures that every true statement within the system can be proven. It guarantees that no provable truths are missed.

Completeness

For all statements $S\in \mathcal{S}$, if $\tau (S)=1$ (the statement is true), then there exists a proof $P\in \mathcal{P}$ such that $\varphi (S,P)=1$ (the proof is accepted).

• The Sudoku Example and Completeness: The Sudoku example from the previous section illustrated a lack of completeness. We didn’t have a general system to prove all true instances of unsolvable Sudoku puzzles. We could demonstrate unsolvability for specific instances, but we lacked a universally applicable method.

• “Predicate Logic” to Define Completeness: Similar to soundness, using predicate logic ((e.g., $\forall S\in \mathcal{S}(\exists P\in \mathcal{P}(\varphi (S,P)=1)\leftarrow \tau (S)=1)$)) to define completeness would be circular. We use logic to express the property of completeness, not define it in terms of logical formulas.

Defining a Proof System

A proof system, denoted as $\Pi =(\mathcal{S},\mathcal{P},\tau ,\varphi )$, consists of:

• Statements ($\mathcal{S}$): The set of all possible statements, representable as bit strings ($\mathcal{S}=\{0,1{\}}^{\ast }$).
• Proofs ($\mathcal{P}$): The set of all possible proofs, also representable as bit strings ($\mathcal{P}=\{0,1{\}}^{\ast }$).
• Semantics ($\tau$): A function $\tau :\mathcal{S}\to \{0,1\}$ assigning truth values to statements.
• Verification Function ($\varphi$): A function $\varphi :\mathcal{S}\times \mathcal{P}\to \{0,1\}$ determining proof validity.

The set of true statements within a proof system is defined as $\{S\in \mathcal{S}\mid \tau (S)=1\}$.

In theoretical computer science, this set is often referred to as a language ($L$), and the question of whether a given string $x$ belongs to the language ($x\in L$) is equivalent to asking if the corresponding statement is true.

Efficiency and Asymptotic Thinking:

We often analyze proof systems in terms of their efficiency as the size of the statements grows (asymptotic analysis). For instance, in Sudoku, the size of the puzzle could vary. Similarly, when considering prime numbers, the length of the bit string representing the number can increase.

A key requirement for a practical proof system is an efficient verification function. In theoretical computer science, “efficient” typically means that the runtime of $\varphi$ is polynomial in the length of the input ($S$ and $P$).

Complexity Classes P and NP:

• NP (Nondeterministic Polynomial Time): NP is the class of languages (or problems) for which there exist proof systems with polynomial-time verification functions. Given a statement $S$ and a proof $P$, we can verify $\varphi (S,P)$ in polynomial time. Examples include Sudoku and compositeness (proving a number is not prime).

• P (Polynomial Time): P is a subclass of NP. A problem is in P if there is a polynomial time algorithm which can solve this problem. Thus, no proof $P$ is needed. This implies the verification is also in polynomial time, so every problem that is in P is also in NP.

The relationship between P and NP is a fundamental open question in computer science. If $P=NP$, every problem for which proofs can be verified in polynomial time can also be solved in polynomial time by a deterministic algorithm. The Primes is in P paper from the previous section proves that primality testing belongs to the complexity class P, hence to NP.

Example: Primality and Compositeness as Proof Systems

We can illustrate the concepts of proof systems, soundness, completeness, and complexity using the examples of proving primality (a number is prime) and compositeness (a number is not prime).

1. Proving Compositeness (Not Prime)

Proving compositeness is relatively straightforward and computationally efficient (it’s in P).

• Statements ($\mathcal{S}$): Bit strings representing integers.
• Semantics ($\tau$): $\tau (S)=1$ if the integer represented by $S$ is composite; 0 otherwise.
• Proofs ($\mathcal{P}$): Bit strings representing integers.
• Verification Function ($\varphi$): $\varphi (S,P)=1$ if the integer represented by $P$ is a non-trivial divisor (a factor other than 1 and the number itself) of the integer represented by $S$ ; 0 otherwise. This involves checking if the remainder of the division is zero, which can be done efficiently in polynomial time.

Soundness and Completeness: This system is both sound and complete:

• Soundness: If a proof $P$ is accepted ($\varphi (S,P)=1$), it means $P$ represents a non-trivial divisor of $S$, which directly implies $S$ is composite ($\tau (S)=1$).
• Completeness: If a statement $S$ is true ($\tau (S)=1$, meaning $S$ is composite), then there exists a non-trivial divisor $P$ such that $\varphi (S,P)=1$.

2. Proving Primality (Is Prime)

Proving primality is more computationally challenging. Simple trial division is not efficient. However, Pratt certificates offer a method for efficiently verifying primality.

• Statements ($\mathcal{S}$): Bit strings representing integers.
• Semantics ($\tau$): $\tau (S)=1$ if the integer represented by $S$ is prime; 0 otherwise.
• Proofs ($\mathcal{P}$): Pratt certificates, which are recursive structures containing prime factorizations and generators (explained below).
• Verification Function ($\varphi$): A function that verifies Pratt certificates (explained below).

Pratt Certificates: A Detailed Look

A Pratt certificate for an integer $n>4$ being prime consists of:

1. Prime Factorization of $n-1$: The certificate provides a prime factorization of $n-1$: $n-1=p_1^{e_1}\cdot p_2^{e_2}\cdot ...\cdot p_k^{e_k}$. Importantly, Pratt certificates for each $p_i$ are also included. This is the recursive step.

2. Generator $g$: A generator $g$ for the multiplicative group ${\mathbb{Z}}_n^{\ast }$.

   • Why a generator? The existence of a generator is crucial. ${\mathbb{Z}}_n^{\ast }$ has a generator if and only if $n$ is 2, 4, $p^k$, or $2p^k$ (where $p$ is an odd prime). For $n>4$, this means ${\mathbb{Z}}_n^{\ast }$ is cyclic if and only if $n$ is a prime power ($p^k$). Furthermore, $|{\mathbb{Z}}_n^{\ast }|=n-1=\varphi (n)$ (Eulers Totient…). This only applies for $n$ prime.

3. Conditions on the Generator:

• $g^{n-1}\equiv 1(\mathrm{mod}n)$ (required by Fermat’s Little Theorem if $n$ is prime).
• $g^{(n-1)/p_i}\not\equiv 1(\mathrm{mod}n)$ for all $p_i$. This condition, together with the previous one, confirms that the order of $g$ is exactly $n-1$, implying $|{\mathbb{Z}}_n^{\ast }|=n-1$, and thus $n$ is prime.

Verification Function ($\varphi$) for Pratt Certificates

1. Base Case: For small $p_i$, use a lookup table to verify primality.
2. Recursive Step:
   • Verify the factorization of $n-1$.
   • Recursively verify the Pratt certificates for each $p_i$.
   • Check the two conditions on the generator $g$.

Limitations of Proof Systems: Scope and Meta-reasoning

Each proof system is inherently limited in its scope. It’s designed to handle a specific type of statement or a particular class of problems. Ideally, we want proof systems with the broadest possible scope, but in practice, they are often specialized. For example, a proof system designed for verifying primality (like Pratt certificates or the AKS test) cannot be directly applied to problems like Sudoku. A key goal in logic is to develop proof systems with the widest possible applicability, but inherent limitations often constrain their scope.

A significant restriction arises when attempting to create “meta-proof systems” – systems that reason about other proof systems. We cannot use a proof system to prove its own correctness. This leads to circular reasoning. To demonstrate the soundness or completeness of a proof system, we require a separate, more powerful proof system.

Why Meta-reasoning Requires a Separate System

Proving a system’s correctness involves demonstrating that it adheres to properties like soundness and completeness. If we attempted to use the system itself for this proof, we’d encounter a circular dependency:

1. The Claim: The proof system is sound (it only proves true statements).
2. The “Proof”: A proof within the system itself that claims the system is sound.
3. The Problem: The “proof” relies on the assumption that the system is sound, which is precisely what we’re trying to prove!

This circularity invalidates the proof. It’s akin to saying, “I am trustworthy because I say I am trustworthy.” To break this cycle, we need an external, independent framework—a separate proof system with greater expressive power—to reason about the original system’s properties.

Intrinsic Limitations

This limitation highlights an intrinsic constraint on formal systems. Gödel’s incompleteness theorems formalize this notion. They demonstrate that any sufficiently complex formal system capable of expressing basic arithmetic will contain true statements that are unprovable within the system itself. This inherent incompleteness reveals fundamental limits on what formal systems can achieve. While we strive for powerful and broadly applicable proof systems, we must acknowledge these intrinsic boundaries.

Dual Asymmetry in Problem Solving

Many problems exhibit a dual asymmetry: finding a solution is often significantly different (and potentially much harder) than demonstrating the absence of a solution. This asymmetry is a recurring theme in computer science and mathematics.

Consider the example of Sudoku discussed earlier:

• Finding a solution: While finding a Sudoku solution might require some effort, strategies like backtracking and constraint satisfaction can be employed. Presenting a solved grid serves as a readily verifiable proof of solvability.
• Proving unsolvability: Demonstrating that a Sudoku puzzle has no solution is considerably more challenging. It requires demonstrating that every possible attempt to complete the puzzle leads to a contradiction. There’s no simple “certificate” of unsolvability analogous to a solved grid.

This asymmetry arises in many other contexts:

• Program Verification: Finding a specific input that crashes a program is often easier than proving that the program never crashes (for all possible inputs).
• Theorem Proving: Finding a mathematical proof of a theorem can be difficult, but demonstrating that a purported proof is incorrect is often much easier (by identifying a flaw in the logic).

This dual asymmetry highlights a fundamental challenge in computer science and mathematics: dealing with the absence or impossibility of something.

Proof Verification and Formats

Proof verification, as embodied by the function $\varphi (S,P)$, can take various forms depending on the nature of the statement, the proof, and the proof system itself. There isn’t a single, universal format.

A common form of verification involves a set of predefined rules and a sequence of steps purported to be a proof. The verification function checks whether each step in the sequence is a valid application of one of the allowed rules. This stepwise, rule-based verification is often encountered in:

• Formal Logic: Proofs in propositional or predicate logic are sequences of formulas, each derived from previous formulas by applying logical inference rules.
• Type Systems: In programming languages, type checking verifies that a program adheres to typing rules, ensuring type safety.
• Formal Verification of Hardware and Software: Model checking and other formal methods use rule-based systems to verify properties of hardware or software designs.

However, not all proof verifications follow this iterative, rule-based structure. The AKS primality test, for example, doesn’t involve checking a sequence of steps against a set of rules. It performs a series of computations, and the outcome of these computations determines whether the input number is prime.

While we’ll primarily focus on rule-based systems for now, it’s essential to remember that proof verification can take many forms, depending on the specific domain and the nature of the problem.

Proof Systems (for Logical Consequence)

Let’s focus on a specific type of proof system where the statement we aim to prove involves logical consequence. These systems are fundamental to many areas of computer science, particularly in formal verification and automated reasoning.

In these systems, a statement $s$ is represented as a pair $(M,G)$, where:

• $M$: A set of formulas representing axioms or assumptions (often called a theory or a knowledge base).
• $G$: A single formula we want to prove (the goal or theorem).

The semantics of such a statement, $\tau (s)$, is defined as follows: $\tau (s)=1⟺M\models G$ This means that $\tau (s)$ is true if and only if the formula $G$ is a logical consequence of the set of formulas $M$. In other words, $G$ must be true in every interpretation or model where all formulas in $M$ are true. This concept of logical consequence is central to many areas of logic and computer science. It captures the idea that $G$ is “provable” or “derivable” from $M$. $M\models G$ is read as ”$M$ logically entails $G$“.

The Universal Nature of Proof Systems

The concept of a proof system, with its components of statements, proofs, and verification, is a fundamental one. While the specific proof systems we construct—the rules, syntax, and verification procedures—are human-made and often arbitrary choices, the underlying idea of a proof system itself is more universal. It reflects our inherent drive to reason, justify, and establish truth.

This is similar to abstract algebra. Concepts like groups, rings, and fields are not arbitrary human inventions. They capture fundamental structural properties that exist independently of us. Mathematicians didn’t create these structures; they discovered and formalized them. The same applies to proof systems. The specific rules of a particular proof system might be human-designed, but the underlying notion of a proof—evidence supporting a claim—is a universal concept that transcends any specific formalization.

Formulas and Logical Consequence: An Example

Let’s explore an example of logical consequence using propositional logic.

We have a set of formulas $M$:

1. $(A\vee Z)\to C$
2. $B\to A$
3. $E\to Z$
4. $(A\wedge C)\to (D\vee E)$
5. $(D\wedge A)\to Z$
6. $A\wedge B$

We want to determine if $M\models Z$ holds—that is, whether the formula $Z$ is a logical consequence of the set of formulas $M$.

Derivation:

1. From (6), we have $A$ and $B$.
2. From (2) and $B$, we can infer $A$ (modus ponens). (We already had A, but this shows how modus ponens would be applied).
3. From (1) and $A$, we get $(A\vee Z)\equiv A$ since $A$ is already true, and thus we have $A\to C$, meaning $C$ is also true (modus ponens).
4. Now we have $A$ and $C$. From (4), $(A\wedge C)\to (D\vee E)$, which, since $A$ and $C$ are true, means we also have $D\vee E$.
5. We now make a case distinction:
   • Case 1: $D$ is true: From (5) and the fact that $A$ and $D$ are true means $Z$.
   • Case 2: $E$ is true: From (3) and $E$, we conclude $Z$ (modus ponens).

Since in both cases we derive $Z$, we conclude that $Z$ is a logical consequence of $M$. Therefore, $M\models Z$ is true, and $\tau ((M,Z))=1$.

It’s crucial to reiterate that while the logical entailment in the previous example was relatively straightforward to determine, this is not always the case. As the complexity of the set of formulas $M$ increases, determining whether $M\models G$ holds becomes significantly more challenging. This difficulty relates to the dual asymmetry discussed earlier: verifying a specific derivation (checking if a given sequence of steps constitutes a valid proof) is often much easier than determining whether a derivation exists in the first place.

Formal Proof Systems and Derivation Rules

To formalize the process of logical deduction, we introduce the concept of derivation rules within a proof system. These rules dictate how we can syntactically manipulate formulas to derive new formulas.

A typical derivation rule is written as:

Premise 1
Premise 2
...
Premise n
-------
Conclusion

This represents a valid inference step: if all the premises hold, then we can conclude the conclusion.

Example: Conjunction Elimination

The rule $F\wedge G⊢F$ (conjunction elimination) states that if we have a formula $F\wedge G$ (the conjunction of $F$ and $G$), then we can derive $F$. Similarly, we can also derive $G$ from the same rule: $F\wedge G⊢G$.

Syntactic Derivation vs. Semantic Entailment

The symbol $⊢$ denotes syntactic derivation. It represents a formal step within a proof system, based purely on the structure of the formulas and the allowed derivation rules. It’s different from $\models$, which represents semantic entailment (logical consequence). Semantic entailment is about truth in all possible interpretations, while syntactic derivation is about manipulating symbols according to rules.

The connection between these two concepts is crucial: a sound and complete proof system ensures that syntactic derivation ($⊢$) accurately reflects semantic entailment ($\models$). In other words, if we can derive $G$ from $M$ using the rules of the system ($M⊢G$), then $G$ must be a logical consequence of $M$ ($M\models G$).

The Goal of a Proof Calculus

We aim to define a proof calculus—a set of derivation rules—such that:

$M⊢G⟹M\models G$

This implication means that if we can derive $G$ from $M$ using the rules of the calculus, then $G$ must logically follow from $M$. This establishes the soundness of the proof system. Completeness, on the other hand, requires the reverse implication: if $M\models G$, then there must exist a derivation $M⊢G$.

By carefully choosing the derivation rules, we can design proof systems that are both sound and complete, ensuring that syntactic manipulation of formulas accurately captures the underlying semantic notion of logical consequence.

Connecting Syntactic Derivation and Semantic Entailment

The relationship between syntactic derivation ($⊢$) and semantic entailment ($\models$) is central to the notion of a sound and complete proof system. A proof calculus (a set of derivation rules) aims to bridge the gap between these two concepts.

• Correctness (Soundness): A proof system is correct (or sound) if every syntactically derivable statement is also semantically entailed. Formally:

  $M⊢G⟹M\models G$

This means that if we can derive $G$ from $M$ using the rules of the calculus, then $G$ must logically follow from $M$. Soundness ensures that the proof system doesn’t allow us to prove false statements. It guarantees that the syntactic manipulations permitted by the rules don’t lead us astray from the truth.

• Completeness: A proof system is complete if every semantically entailed statement is also syntactically derivable. Formally:

  $M\models G⟹M⊢G$

This means that if $G$ is a logical consequence of $M$, then there exists a derivation of $G$ from $M$ using the rules of the calculus. Completeness ensures that the proof system is powerful enough to prove all true statements within its scope. It guarantees that we don’t miss any provable truths.

A proof system that is both sound and complete is ideal. It provides a perfect correspondence between syntactic manipulation of formulas (derivation) and the semantic notion of truth (logical consequence). However, achieving both soundness and completeness can be challenging, and sometimes, depending on the specific application, one property might be prioritized over the other.

Syntactic Derivation Steps

If we look at the example from above, we can formalize the derivation of $Z$ from $M$ using the following rules and steps:

Rules

• $R_1:F\wedge G⊢F$
• $R_2:F⊢F\vee G$
• $R_3:\{F,F\to G\}⊢G$
• $R_4:F,G⊢F\wedge G$
• $R_5:\{(F\wedge G)\to H,G\}⊢F\to H$
• $R_6:\{F\to H,G\to H\}⊢(F\vee G)\to H$

Steps

• $(6){⊢}_{R_1}A$ $(7)$
• $(7){⊢}_{R_2}A\vee Z$ $(8)$
• $(8)(1){⊢}_{R_3}C$ $(9)$
• $(7)(9){⊢}_{R_4}A\wedge C$ $(10)$
• $(10)(4){⊢}_{R_3}D\vee E$ $(11)$
• $(5)(7){⊢}_{R_5}D\to Z$ $(12)$
• $(12)(3){⊢}_{R_6}(D\vee E)\to Z$ $(13)$
• $(11)(13){⊢}_{R_3}Z$