22 Determinants, Permutations, Properties, Cofactors, Cramers Rule

Lecture from 29.11.2024 | Video: Videos ETHZ

Definition and Properties

Introduction

In this lecture, we delve into the concept of determinants, a fundamental function in linear algebra that assigns a scalar value to a square matrix. Determinants play a crucial role in various applications, including solving systems of linear equations, determining the invertibility of matrices, and calculating volumes of geometric objects.

Intro to determinants…

I genuinely suggest you watch this video (and maybe the next few in the playlist) before reading this or watching the lecture…

The Determinant as a Function over Matrices

The determinant is a function defined specifically for square matrices. If $A$ is an $n\times n$ matrix (denoted as $A\in {\mathbb{R}}^{n\times n}$), its determinant, denoted as $\det (A)$, is a real number.

Geometric Interpretation:

The absolute value of the determinant, $|\det (A)|$, represents the volume of the parallelepiped spanned by the column vectors of the matrix $A$. A parallelepiped is the generalization of a parallelogram to higher dimensions. In 2D, it’s a parallelogram; in 3D, it’s a parallelepiped ; and so on.

More formally, if the columns of $A$ are denoted as $A_{\cdot ,1},A_{\cdot ,2},\dots ,A_{\cdot ,n}$, the parallelepiped $P$ is defined as:

$P=\text{vol}\left(\left\{\mathbf{x}\in {\mathbb{R}}^n|\exists 0\le {\lambda }_i\le 1\text{ for }i=1,\dots ,n\text{ such that }\mathbf{x}={\sum }_{i=1}^n{\lambda }_i{A}_{\cdot ,i}\right\}\right)$

This set describes all possible linear combinations of the column vectors of $A$, where the coefficients ${\lambda }_i$ are between 0 and 1. The volume of this region is given by $|\det (A)|$. The sign of the determinant indicates the orientation of the parallelepiped.

Fundamental Properties of Determinants

Determinants possess several key properties that are essential for understanding and working with them:

1. Invertibility: A square matrix $A$ is invertible (i.e., has an inverse matrix $A^{-1}$) if and only if its determinant is non-zero: $\det (A)\ne 0$. This is a crucial connection between the determinant and the solvability of linear systems.

2. Determinant of the Transpose: The determinant of a matrix is equal to the determinant of its transpose: $\det (A)=\det (A^T)$. The transpose of a matrix is obtained by interchanging its rows and columns.

3. Linearity: The determinant is a linear function of each row (or each column) of the matrix when the other rows (or columns) are held fixed. More formally:

   Let $A$ and $B$ be two $n\times n$ matrices that are identical except for their $i$-th row. Let $C$ be an $n\times n$ matrix such that all rows of $C$ are the same as the corresponding rows of $A$ (and $B$) except for the $i$-th row where we have:

   $C_{i,\cdot }=A_{i,\cdot }+B_{i,\cdot }$

   Then,

   $\det (C)=\det (A)+\det (B)$

   This property means that we can “split” a determinant calculation if one row is a sum of two vectors.

4. Multiplicativity: The determinant of the product of two matrices is equal to the product of their determinants: $\det (AB)=\det (A)\det (B)$. This property is extremely useful in various proofs and calculations.

These four properties are fundamental to the theory of determinants. We’ll use them to derive further results and computational methods.

2x2 Matrices and Proofs

Determinants of 2x2 Matrices

For a $2\times 2$ matrix $A=\left[\begin{array}{cc}a& c\\ b& d\end{array}\right]$, the determinant is defined as:

$\det (A)=ad-bc$

This simple formula allows us to easily calculate the determinant of any $2\times 2$ matrix.

Example:

$\det \left(\left[\begin{array}{cc}3& 2\\ -1& 4\end{array}\right]\right)=(3)(4)-(2)(-1)=12+2=14$

Lemma: $|\det (A)|=\text{vol}(P)$

Let $A=\left[\begin{array}{cc}a& c\\ b& d\end{array}\right]$. The absolute value of the determinant of $A$ is equal to the volume (area in this case) of the parallelogram $P$ spanned by the column vectors of $A$. The vertices of the parallelogram are (0,0), (a,b), (c,d), and (a+c, b+d).

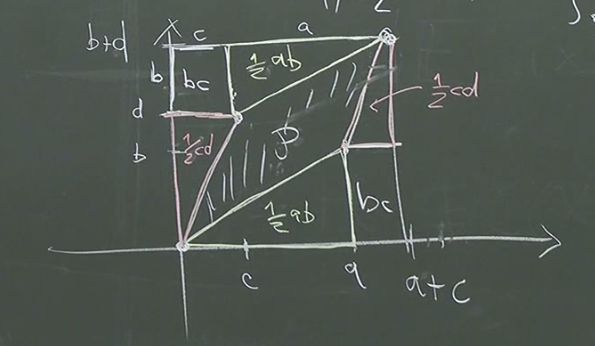
We can calculate the area of $P$ by finding the area of the large rectangle enclosing the parallelogram and subtracting the areas of the four triangles and two small rectangles: (Note that two of the triangles are congruent, and the other two are also congruent).

Taking the absolute value to account for possible negative orientation: $\text{vol}(P)=|ad-bc|=|\det (A)|$

Thus, the absolute value of the determinant of a $2\times 2$ matrix represents the area of the parallelogram formed by its column vectors.

Proof of Multiplicativity for 2x2 Matrices

Let’s prove the multiplicativity property ($\det (AW)=\det (A)\det (W)$) for $2\times 2$ matrices.

Let $A=\left[\begin{array}{cc}a& c\\ b& d\end{array}\right]$ and $W=\left[\begin{array}{cc}x& z\\ y& w\end{array}\right]$. Then:

$AW=\left[\begin{array}{cc}ax+cy& az+cw\\ bx+dy& bz+dw\end{array}\right]$

Now, let’s calculate the determinant of $AW$:

(Notice how the terms $axbz$ and $-azbx$ cancel out, as do $-cwdy$ and $cydw$).

We can rearrange this expression:

This proves the multiplicativity property for $2\times 2$ matrices.

Characterizing Invertibility of 2x2 Matrices using the Determinant

Lemma: A $2\times 2$ matrix $A$ is invertible if and only if $\det (A)\ne 0$.

Proof:

(Forward direction): If $A$ is invertible, it has an inverse $A^{-1}$ such that $A{A}^{-1}=I$ (the identity matrix). Using the multiplicativity property:

$\det (A{A}^{-1})=\det (A)\det (A^{-1})=\det (I)=1$

Since the product $\det (A)\det (A^{-1})$ equals 1, neither determinant can be zero. Thus, $\det (A)\ne 0$.

(Reverse direction): Assume $\det (A)=ad-bc\ne 0$. Without loss of generality, let’s assume $a\ne 0$. (If $a=0$, then $b$ must be non-zero, and we can use a similar argument).

Consider the system of linear equations $AW=I$:

$\left[\begin{array}{cc}a& c\\ b& d\end{array}\right]\left[\begin{array}{cc}x& z\\ y& w\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$

This gives us the following equations:

From the first and third equations, we can solve for x and z (since we assumed $a\ne 0$):

$x=\frac{1-cy}{a},z=\frac{-cw}{a}$

Substitute $x=\frac{1-cy}{a}$ into the second equation ($bx+dy=0$) and simplify:

$b\left(\frac{1-cy}{a}\right)+dy=0\Rightarrow b(1-cy)+ady=0\Rightarrow y(ad-bc)=-b\Rightarrow y=\frac{-b}{ad-bc}$

We can find a similar solution for w. The existence of these solutions for $x$, $y$, $z$, and $w$ demonstrates that $A^{-1}$ exists, so $A$ is invertible.

This completes the proof that a $2\times 2$ matrix is invertible if and only if its determinant is non-zero. This result will generalize to higher dimensions.

Permutations and Higher Dimensions

Defining Determinants using Permutations…

Once again, I suggest watching this before reading this or watching the lecture…

The $n\times n$ Case: Permutations

To define the determinant for general $n\times n$ matrices, we need the concept of permutations.

Definition (Permutation): A permutation of the set $\{1,2,\dots ,n\}$ is a bijective function $\sigma :\{1,2,\dots ,n\}\to \{1,2,\dots ,n\}$. In other words, it’s a reordering of the numbers from 1 to $n$. The set of all permutations of $n$ elements is denoted by ${\Pi }_n$.

Example: For $n=3$, one possible permutation is $\sigma (1)=2$, $\sigma (2)=3$, $\sigma (3)=1$.

Definition (Sign of a Permutation):

The sign of a permutation $\sigma$, denoted as $\text{sgn}(\sigma )$, is either +1 or -1. It’s determined by the number of inversions in the permutation. An inversion is a pair of elements $(i,j)$ such that $i<j$ but $\sigma (i)>\sigma (j)$.

• If the number of inversions is even, $\text{sgn}(\sigma )=+1$.
• If the number of inversions is odd, $\text{sgn}(\sigma )=-1$.

Example:

Let’s find the sign of the permutation $\pi$ where $\pi (1)=1$, $\pi (2)=3$, $\pi (3)=2$, $\pi (4)=4$. The pairs $(i,j)$ with $i<j$ are:

(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)

Comparing the permuted values:

• $\pi (1)<\pi (2)$ (1 < 3)
• $\pi (1)<\pi (3)$ (1 < 2)
• $\pi (1)<\pi (4)$ (1 < 4)
• $\pi (2)>\pi (3)$ (3 > 2) - This is an inversion!
• $\pi (2)<\pi (4)$ (3 < 4)
• $\pi (3)<\pi (4)$ (2 < 4)

There’s only one inversion, so $\text{sgn}(\pi )=-1$.

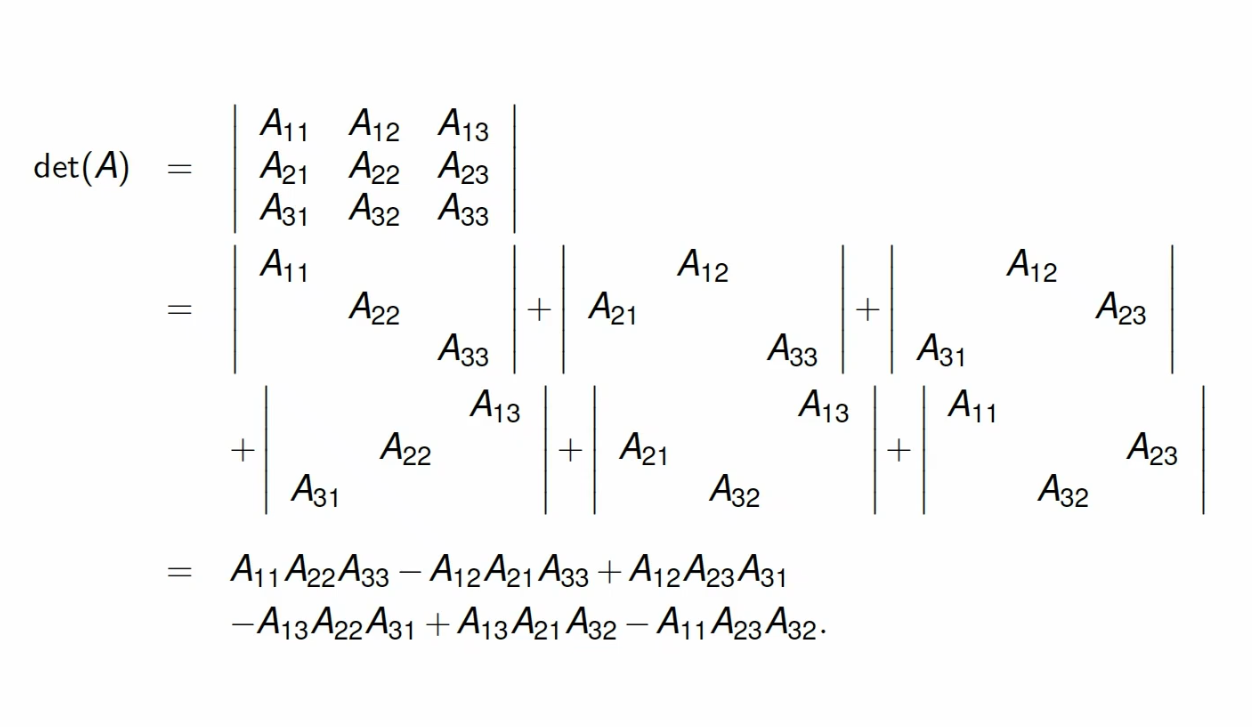
Definition of the Determinant for $n\times n$ Matrices

Using permutations, we can define the determinant of an $n\times n$ matrix $A$ as:

$\det (A)={\sum }_{\sigma \in {\Pi }_n}\text{sgn}(\sigma ){\prod }_{i=1}^n{A}_{i,\sigma (i)}$

This formula calculates the determinant as a sum over all possible permutations of the columns. Each term in the sum is a product of entries from the matrix, one from each row and each column, with the sign determined by the permutation.

Remarks:

1. Multiplicativity of the Sign: For any two permutations $\sigma$ and $\gamma$, $\text{sgn}(\sigma \circ \gamma )=\text{sgn}(\sigma )\text{sgn}(\gamma )$, where $\sigma \circ \gamma$ denotes the composition of the two permutations.

2. Equal Number of Positive and Negative Signs: For $n\ge 2$, exactly half of the permutations in ${\Pi }_n$ have a sign of +1, and the other half have a sign of -1.

3. Determinant of Permutation Matrices: A permutation matrix $P$ is a matrix obtained by permuting the rows (or columns) of the identity matrix. The determinant of a permutation matrix is equal to the sign of the corresponding permutation: $\det (P)=\text{sgn}(\sigma )$, where $\sigma$ is the permutation represented by $P$.

4. Determinant of a $1\times 1$ Matrix: For a $1\times 1$ matrix $A=[a]$, there’s only one permutation (the identity), and its sign is +1. Therefore, $\det (A)=a$.

Determinant of the Transpose and Further Observations

Further Observations

1. Determinants of $2\times 2$ Matrices Revisited:

Let’s revisit the determinant of a $2\times 2$ matrix in light of our new definition using permutations. For a $2\times 2$ matrix $A$, there are two permutations:

• ${\sigma }_1$: the identity permutation (${\sigma }_1(1)=1$, ${\sigma }_1(2)=2$), with $\text{sgn}({\sigma }_1)=+1$
• ${\sigma }_2$: the permutation that swaps the two elements (${\sigma }_2(1)=2$, ${\sigma }_2(2)=1$), with $\text{sgn}({\sigma }_2)=-1$

Applying the determinant formula:

$\det (A)=\text{sgn}({\sigma }_1)A_{1,1}{A}_{2,2}+\text{sgn}({\sigma }_2)A_{1,2}{A}_{2,1}=A_{1,1}{A}_{2,2}-A_{1,2}{A}_{2,1}$

This matches our earlier formula: $ad-bc$.

2. Determinant of Triangular Matrices:

For a triangular matrix (either upper or lower triangular), the determinant is the product of the diagonal entries.

Let $T\in {\mathbb{R}}^{n\times n}$ be a triangular matrix. Then:

$\det (T)={\prod }_{k=1}^n{T}_{k,k}$

Proof: In a triangular matrix, all entries below (or above) the main diagonal are zero. When we expand the determinant using permutations, the only non-zero term in the sum will be the product of the diagonal entries, which corresponds to the identity permutation. All other permutations will involve at least one zero entry, making the product zero. The determinant of the identity matrix is 1, since there’s only one permutation and the product of the diagonal elements is 1.

Theorem: Determinant of the Transpose

Theorem: For any square matrix $A\in {\mathbb{R}}^{n\times n}$, $\det (A^T)=\det (A)$.

This theorem states a fundamental property: the determinant of a matrix is equal to the determinant of its transpose. The transpose of a matrix is obtained by swapping its rows and columns.

Proof

1. Inverse Permutation

• Definition: For a permutation $\sigma$, its inverse ${\sigma }^{-1}$ reverses the mapping: if $\sigma$ sends $i$ to $j$ ($\sigma (i)=j$), then ${\sigma }^{-1}$ sends $j$ back to $i$ (${\sigma }^{-1}(j)=i$).
• Key Property: Equal Signs: The sign of a permutation is the same as the sign of its inverse: $\text{sgn}(\sigma )=\text{sgn}({\sigma }^{-1})$.
• Why Equal Signs?
  • Applying a permutation and then its inverse gets us back to the original order: $\sigma \circ {\sigma }^{-1}=\text{id}$, where ‘id’ is the identity permutation (leaving everything in place).
  • The identity permutation has no inversions, so its sign is $+1$: $sgn(id)=1$.
  • The sign of a composition of permutations is the product of their signs: $\text{sgn}(\sigma \circ {\sigma }^{-1})=\text{sgn}(\sigma )\text{sgn}({\sigma }^{-1})$.
  • Combining these facts: $\text{sgn}(\sigma )\text{sgn}({\sigma }^{-1})=1$. Since the sign can only be +1 or -1, both $\sigma$ and ${\sigma }^{-1}$ must have the same sign.

2. Determinant of the Transpose

• Definition of Transpose: Recall that the transpose $A^T$ of a matrix $A$ has entries $(A^T{)}_{ij}=A_{ji}$. Rows become columns, and columns become rows.

• Determinant Formula for the Transpose: Using the definition of the determinant and the property of the transpose, we have:

  $\det (A^T)={\sum }_{\sigma \in {\Pi }_n}\text{sgn}(\sigma ){\prod }_{i=1}^n(A^T{)}_{i,\sigma (i)}={\sum }_{\sigma \in {\Pi }_n}\text{sgn}(\sigma ){\prod }_{i=1}^n{A}_{\sigma (i),i}$

• Focus on the Product: The key difference from $\det (A)$ is the order of indices in the product: $A_{\sigma (i),i}$ instead of $A_{i,\sigma (i)}$.

3. Change of Index (Clever Trick)

• Relabeling: Let $j=\sigma (i)$. Then, $i={\sigma }^{-1}(j)$. As $i$ goes from 1 to $n$, so does $j$ (because $\sigma$ is a bijection—a one-to-one mapping).

• Rewriting the Product: This relabeling allows us to rewrite the product:

  ${\prod }_{i=1}^n{A}_{\sigma (i),i}={\prod }_{j=1}^n{A}_{j,{\sigma }^{-1}(j)}$

  We’ve essentially switched the roles of the row and column indices by using the inverse permutation.

4. Rewriting the Sum (Using the Key Property)

• Substituting the Sign: We know that $\text{sgn}(\sigma )=\text{sgn}({\sigma }^{-1})$. Substituting this into the determinant formula for $A^T$:

  $\det (A^T)={\sum }_{\sigma \in {\Pi }_n}\text{sgn}({\sigma }^{-1}){\prod }_{j=1}^n{A}_{j,{\sigma }^{-1}(j)}$

  We are summing the same terms as in $\det (A)$ but in a different order. Since addition is commutative, the sum is unchanged.

5. Same as Determinant of A (Relabeling the Sum)

• Since we sum over all permutations, summing over $\sigma$ is the same as summing over ${\sigma }^{-1}$. Let’s just call ${\sigma }^{-1}$ as $\gamma$:

  $\det (A^T)={\sum }_{\gamma \in {\Pi }_n}\text{sgn}(\gamma ){\prod }_{j=1}^n{A}_{j,\gamma (j)}$

• This is now exactly the definition of $\det (A)$!

Therefore, $\det (A^T)=\det (A)$.

General Properties and Co-factors

General Properties of the Determinant Operator

We now delve into some crucial properties of the determinant that extend beyond the specific cases we’ve examined so far.

Theorem

1. Invertibility: A matrix $A\in {\mathbb{R}}^{n\times n}$ is invertible if and only if $\det (A)\ne 0$. We proved this for the $2\times 2$ case; the proof for the general case is more involved and relies on concepts we’ll develop later. This also means that if $\det (A)=0$, the matrix is singular (not invertible). It indicates that the columns (or rows) of A are linearly dependent, and the matrix does not have full rank.

2. Multiplicativity: For any two matrices $A,B\in {\mathbb{R}}^{n\times n}$, $\det (AB)=\det (A)\det (B)$. The proof for the general $n\times n$ case requires more advanced techniques beyond the scope of this lecture, but relies on the properties of permutations and matrix multiplication. This property implies that the determinant respects matrix multiplication; the determinant of a product is the product of the determinants. This is crucial for understanding how determinants change under transformations.

3. Determinant of the Inverse: If $A$ is invertible (i.e., $\det (A)\ne 0$), then

   $\det (A^{-1})=\frac{1}{\det (A)}$

   This follows directly from the multiplicativity property: $\det (A)\det (A^{-1})=\det (A{A}^{-1})=\det (I)=1$, so $\det (A^{-1})$ must be the reciprocal of $\det (A)$.

Lemma: Determinant of Orthogonal Matrices

Lemma: If $Q\in {\mathbb{R}}^{n\times n}$ is an orthogonal matrix, then $\det (Q)=\pm 1$.

Definition: Recall that a square matrix $Q$ is orthogonal if its transpose is equal to its inverse: $Q^T=Q^{-1}$. This also implies that $Q^{T}Q=Q{Q}^T=I$. Geometrically, orthogonal transformations preserve lengths and angles.

Proof

1. Determinant of the Identity: The determinant of the identity matrix $I$ is 1: $\det (I)=1$. This is because the only non-zero term in the permutation expansion of the determinant is the product of the diagonal elements, which are all 1, associated with the identity permutation (which has a sign of +1).

2. Orthogonality Property: Since $Q$ is orthogonal, we have $Q^{T}Q=I$.

3. Determinant of the Product: Using the property that the determinant of a product is the product of the determinants: $\det (Q^{T}Q)=\det (Q^T)\det (Q)$

4. Determinant of the Transpose: We know that $\det (Q^T)=\det (Q)$. Therefore: $\det (Q^{T}Q)=\det (Q)\det (Q)=(\det (Q){)}^2$

5. Combining Results: Combining the above results, we have: $(\det (Q){)}^2=\det (I)=1$

6. Solving for det(Q): Taking the square root of both sides: $|\det (Q)|=1$ This means that $\det (Q)$ can be either +1 or -1.

Therefore, the determinant of an orthogonal matrix is either +1 or -1. This result reflects the fact that orthogonal transformations preserve volume (they don’t stretch or shrink space), but they can potentially change the orientation (hence the possibility of a negative determinant).

Orthogonal matrices with determinant +1 represent rotations, while those with determinant -1 represent reflections or combinations of rotations and reflections.

3 x 3 Matrices: Explicit Calculation using Permutations

Let’s apply the determinant definition using permutations to a $3\times 3$ matrix. This will give us a concrete formula for calculating the determinant in this common case.

A $3\times 3$ matrix has $3!=6$ permutations. Let’s list them and their signs:

Now, applying the determinant formula: $\det (A)={\sum }_{\sigma \in {\Pi }_3}\text{sgn}(\sigma ){\prod }_{i=1}^3{A}_{i,\sigma (i)}$

We get:

$\det (A)=A_{11}{A}_{22}{A}_{33}-A_{11}{A}_{23}{A}_{32}-A_{12}{A}_{21}{A}_{33}+A_{12}{A}_{23}{A}_{31}+A_{13}{A}_{21}{A}_{32}-A_{13}{A}_{22}{A}_{31}$

This formula can be remembered using the “Sarrus’ rule” or the “Rule of Sarrus,” a visual mnemonic device:

A11 A12 A13   A11 A12
A21 A22 A23   A21 A22    
A31 A32 A33   A31 A32

// Diagonals going down to the right are positive:
+ A11*A22*A33 + A12*A23*A31 + A13*A21*A32  

// Diagonals going down to the left are negative:
- A13*A22*A31 - A11*A23*A32 - A12*A21*A33

While Sarrus’ rule is handy for $3\times 3$ matrices, it doesn’t generalize to higher dimensions. The general formula using permutations is the fundamental definition for all $n\times n$ matrices.

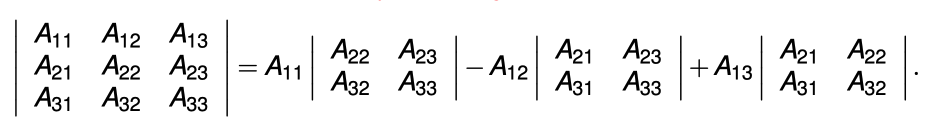
This 3x3 example provides a concrete illustration of how the permutation-based definition works in practice. It shows how to enumerate the permutations and calculate the corresponding products with the correct signs to compute the determinant.

Co-factors

Definition (Co-factor):

Let $A\in {\mathbb{R}}^{n\times n}$. For each $1\le i,j\le n$, let $A_{ij}$ denote the $(n-1)\times (n-1)$ matrix obtained by deleting the $i$-th row and $j$-th column of $A$. The cofactor $C_{ij}$ of $A$ is defined as:

$C_{ij}=(-1{)}^{i+j}\det (A_{ij})$

The cofactor is a signed determinant of a smaller matrix, and the sign is determined by the position of the element in the original matrix. The $(-1{)}^{i+j}$ factor creates a checkerboard pattern of positive and negative signs.

Lemma (Laplace Expansion): The determinant of a matrix $A$ can be computed by expanding along any row or column using cofactors. Expansion along row $i$: $\det (A)={\sum }_{j=1}^n{A}_{ij}{C}_{ij}$ Expansion along column $j$: $\det (A)={\sum }_{i=1}^n{A}_{ij}{C}_{ij}$

This lemma provides a recursive way to calculate determinants by reducing the problem to calculating determinants of smaller matrices.

Lemma: Adjugate Matrix and Inverse

Definition: Adjugate Matrix The adjugate matrix $\text{adj}(A)$ of a matrix $A$ is the transpose of the cofactor matrix $C$: $\text{adj}(A)=C^T$, so that the $(i,j)$ entry of $\text{adj}(A)$ is $C_{ji}$.

Lemma: Given a matrix $A\in {\mathbb{R}}^{n\times n}$ with $\det (A)\ne 0$, let $C$ be the matrix of cofactors of $A$. Then: $A^{-1}=\frac{1}{\det (A)}{C}^T=\frac{1}{\det (A)}\text{adj}(A)$ In other words, we have: $A{C}^T=\det (A)I$ This formula provides an explicit way to calculate the inverse of a matrix using its cofactors. The proof utilizes the Laplace expansion and properties of the cofactor matrix which are beyond the scope of these notes.

Cramer’s Rule, Linearity, and Example

Cramer’s Rule: A Formula for Linear Systems

Cramer’s Rule provides a method for solving systems of linear equations using determinants.

Theorem (Cramer’s Rule):

Let $A\in {\mathbb{R}}^{n\times n}$ be an invertible matrix (i.e., $\det (A)\ne 0$), and let $\mathbf{b}\in {\mathbb{R}}^n$. Then the solution $\mathbf{x}\in {\mathbb{R}}^n$ to the linear system $A\mathbf{x}=\mathbf{b}$ is given by:

$x_j=\frac{\det (B_j)}{\det (A)},j=1,2,\dots ,n$

where $B_j$ is the matrix obtained by replacing the $j$-th column of $A$ with the vector $\mathbf{b}$.

Example (n = 3):

Consider the system $A\mathbf{x}=\mathbf{b}$:

To find $x_1$, we replace the first column of $A$ with $\mathbf{b}$:

Then, $x_1=\frac{\det (B_1)}{\det (A)}$. Similarly, we can find $x_2$ and $x_3$ by replacing the second and third columns of $A$ with $\mathbf{b}$, respectively.

Proof Idea: Cramer’s rule follows from the formula for the inverse of a matrix using the adjugate matrix and the fact that $x=A^{-1}b$. Consider the $j^{th}$ entry of the solution vector $\mathbf{x}$ given by: $x_j=(A^{-1}b{)}_j$. Using the expression for the inverse in terms of the adjugate, we have: $x_j=\frac{1}{\det (A)}{\sum }_{i=1}^n{C}_{ji}{b}_i$ This is exactly the formula for $\frac{\det (B_j)}{\det (A)}$ using the Laplace expansion along the $j^{th}$ column.

Linearity of the Determinant

Lemma: The determinant is a linear function of each row (or column). For any scalars ${\alpha }_0,{\alpha }_1\in \mathbb{R}$ and vectors ${\mathbf{a}}_0,{\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_n\in {\mathbb{R}}^n$:

The same holds for any column. This property was stated earlier; it follows directly from the definition of the determinant as a sum over permutations since each term in the sum will contain exactly one element from each row and each column.