19 Gram-Schmidt Process, QR-Decomposition, Properties of Q and R

Lecture from 20.11.2024 | Video: Videos ETHZ

This lecture covers the Gram-Schmidt process for orthonormalizing a set of vectors and the concept of the pseudoinverse, a generalization of the matrix inverse for non-square or singular matrices.

Preparations for the Gram-Schmidt Process

Task

Given a subspace $S$ of ${\mathbb{R}}^m$ spanned by a basis ${\mathbf{a}}_1,\dots ,{\mathbf{a}}_n$ (i.e., $S=\text{Span}({\mathbf{a}}_1,\dots ,{\mathbf{a}}_n)$), our goal is to construct an orthonormal basis for $S$.

The Idea (Two Vectors)

To illustrate the Gram-Schmidt process, consider a subspace spanned by two vectors ${\mathbf{a}}_1$ and ${\mathbf{a}}_2$.

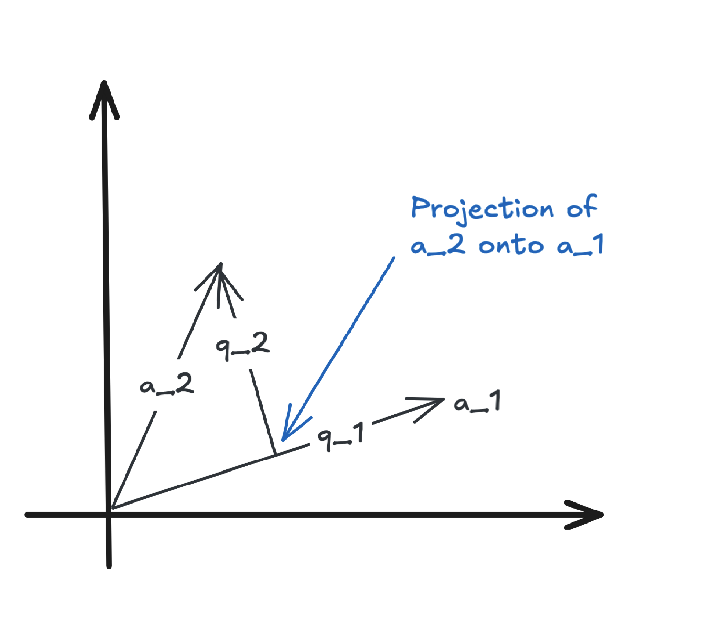
Steps:

1. Normalization: Normalize the first vector ${\mathbf{a}}_1$ to obtain: ${\mathbf{q}}_1=\frac{{\mathbf{a}}_1}{\Vert {\mathbf{a}}_1\Vert }.$

2. Orthogonalization: Subtract the projection of ${\mathbf{a}}_2$ onto ${\mathbf{q}}_1$ from ${\mathbf{a}}_2$: ${\mathbf{v}}_2={\mathbf{a}}_2-({\mathbf{a}}_2^T{\mathbf{q}}_1){\mathbf{q}}_1.$ This ensures ${\mathbf{v}}_2$ is orthogonal to ${\mathbf{q}}_1$.

   • Key observation: ${\mathbf{v}}_2\ne 0$ because ${\mathbf{a}}_1$ and ${\mathbf{a}}_2$ are linearly independent.

3. Normalization: Normalize ${\mathbf{v}}_2$ to obtain: ${\mathbf{q}}_2=\frac{{\mathbf{v}}_2}{\Vert {\mathbf{v}}_2\Vert }.$

Claim: ${\mathbf{q}}_1$ and ${\mathbf{q}}_2$ are orthonormal.

1. Normalization: By construction, $\Vert {\mathbf{q}}_1\Vert =1$ and $\Vert {\mathbf{q}}_2\Vert =1$.

2. Orthogonality: By definition of ${\mathbf{v}}_2$, the projection of ${\mathbf{a}}_2$ onto ${\mathbf{q}}_1$ is removed, leaving ${\mathbf{v}}_2$ orthogonal to ${\mathbf{q}}_1$. To show this explicitly: ${\mathbf{q}}_1^T{\mathbf{q}}_2=\frac{1}{\Vert {\mathbf{v}}_2\Vert }{\mathbf{q}}_1^T({\mathbf{a}}_2-({\mathbf{a}}_2^T{\mathbf{q}}_1){\mathbf{q}}_1).$

   Expanding this: ${\mathbf{q}}_1^T{\mathbf{q}}_2=\frac{1}{\Vert {\mathbf{v}}_2\Vert }\left({\mathbf{q}}_1^T{\mathbf{a}}_2-{\mathbf{a}}_2^T{\mathbf{q}}_1\cdot {\mathbf{q}}_1^T{\mathbf{q}}_1\right).$

   Since ${\mathbf{q}}_1^T{\mathbf{q}}_1=1$ and ${\mathbf{a}}_2^T{\mathbf{q}}_1={\mathbf{q}}_1^T{\mathbf{a}}_2$, this simplifies to: ${\mathbf{q}}_1^T{\mathbf{q}}_2=0.$

Thus, ${\mathbf{q}}_1$ and ${\mathbf{q}}_2$ are orthogonal, and since they are also normalized, they form an orthonormal set.

The Gram-Schmidt process works by systematically orthogonalizing and normalizing vectors in a given basis. This ensures the resulting vectors are both orthogonal and of unit length, creating an orthonormal basis for the subspace $S$.

The process can be extended to any number of vectors, ensuring that each new vector is orthogonal to all previously processed vectors in the set.

The Gram-Schmidt Process

The Gram-Schmidt process is an algorithm for orthonormalizing a set of linearly independent vectors. It transforms a set of vectors ${\mathbf{a}}_1,\dots ,{\mathbf{a}}_n$ that span a subspace $S$ into an orthonormal basis ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_n$ for the same subspace.

Intuition

The process works by iteratively constructing orthonormal vectors from the original basis vectors:

1. Start by normalizing the first vector ${\mathbf{a}}_1$ to create ${\mathbf{q}}_1$.
2. For each subsequent vector ${\mathbf{a}}_k$, subtract its projection onto the subspace spanned by the previously constructed orthonormal vectors ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$.
3. This subtraction removes all components of ${\mathbf{a}}_k$ that lie in the directions of the existing ${\mathbf{q}}_i$. What remains is a vector orthogonal to all previous ${\mathbf{q}}_i$.
4. Normalize this orthogonal vector to obtain the next orthonormal vector, ${\mathbf{q}}_k$.

This iterative approach guarantees that the resulting set $\{{\mathbf{q}}_1,\dots ,{\mathbf{q}}_n\}$ is orthonormal and spans the same subspace $S$ as the original set $\{{\mathbf{a}}_1,\dots ,{\mathbf{a}}_n\}$.

Gram-Schmidt Algorithm

1. Initialize: Normalize the first vector to obtain:
   ${\mathbf{q}}_1=\frac{{\mathbf{a}}_1}{\Vert {\mathbf{a}}_1\Vert }$

2. Iterate: For $k=2,\dots ,n$:

   • Orthogonalize: Subtract the projection of ${\mathbf{a}}_k$ onto the subspace spanned by ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$:
     ${\mathbf{d}}_k={\mathbf{a}}_k-{\sum }_{i=1}^{k-1}({\mathbf{a}}_k^T{\mathbf{q}}_i){\mathbf{q}}_i$
   • Normalize: Normalize the resulting orthogonal vector:
     ${\mathbf{q}}_k=\frac{{\mathbf{d}}_k}{\Vert {\mathbf{d}}_k\Vert }$

Proof of Correctness (by Induction)

We will prove by induction that for each $k$, the vectors ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_k$ form an orthonormal basis for $S_k=\text{Span}({\mathbf{a}}_1,\dots ,{\mathbf{a}}_k)$.

Base Case ($k=1$):

1. The vector ${\mathbf{q}}_1$ is defined as:
   ${\mathbf{q}}_1=\frac{{\mathbf{a}}_1}{\Vert {\mathbf{a}}_1\Vert }$
   Since ${\mathbf{q}}_1$ is scaled to have unit length, $\Vert {\mathbf{q}}_1\Vert =1$.

2. The span of ${\mathbf{q}}_1$ is equal to $S_1$ because ${\mathbf{q}}_1$ is a scalar multiple of ${\mathbf{a}}_1$.

Thus, ${\mathbf{q}}_1$ forms an orthonormal basis for $S_1$.

Inductive Hypothesis:

Assume that ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$ form an orthonormal basis for $S_{k-1}=\text{Span}({\mathbf{a}}_1,\dots ,{\mathbf{a}}_{k-1})$.

Inductive Step ($k$):

We need to show that:

1. ${\mathbf{q}}_k$ has unit length.
2. ${\mathbf{q}}_k$ is orthogonal to ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$.
3. ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_k$ span $S_k$.

1. ${\mathbf{q}}_k$ has unit length:

By construction, ${\mathbf{q}}_k$ is defined as:

${\mathbf{q}}_k=\frac{{\mathbf{d}}_k}{\Vert {\mathbf{d}}_k\Vert },\text{where }{\mathbf{d}}_k={\mathbf{a}}_k-{\sum }_{i=1}^{k-1}({\mathbf{a}}_k^T{\mathbf{q}}_i){\mathbf{q}}_i.$
Since ${\mathbf{q}}_k$ is normalized, its length is:

$\Vert {\mathbf{q}}_k\Vert =\Vert \frac{{\mathbf{d}}_k}{\Vert {\mathbf{d}}_k\Vert }\Vert =1.$

2. ${\mathbf{q}}_k$ is orthogonal to ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$:

To prove this, consider any $j<k$:

${\mathbf{q}}_j^T{\mathbf{q}}_k={\mathbf{q}}_j^T\frac{{\mathbf{d}}_k}{\Vert {\mathbf{d}}_k\Vert }.$

Substitute ${\mathbf{d}}_k$:

${\mathbf{q}}_j^T{\mathbf{q}}_k=\frac{1}{\Vert {\mathbf{d}}_k\Vert }{\mathbf{q}}_j^T\left({\mathbf{a}}_k-{\sum }_{i=1}^{k-1}({\mathbf{a}}_k^T{\mathbf{q}}_i){\mathbf{q}}_i\right).$

Distribute the dot product:

${\mathbf{q}}_j^T{\mathbf{q}}_k=\frac{1}{\Vert {\mathbf{d}}_k\Vert }\left({\mathbf{q}}_j^T{\mathbf{a}}_k-{\sum }_{i=1}^{k-1}({\mathbf{a}}_k^T{\mathbf{q}}_i){\mathbf{q}}_j^T{\mathbf{q}}_i\right).$

Since ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$ are orthonormal, ${\mathbf{q}}_j^T{\mathbf{q}}_i=0$ for $i\ne j$, and ${\mathbf{q}}_j^T{\mathbf{q}}_j=1$. This simplifies to:

${\mathbf{q}}_j^T{\mathbf{q}}_k=\frac{1}{\Vert {\mathbf{d}}_k\Vert }\left({\mathbf{q}}_j^T{\mathbf{a}}_k-({\mathbf{a}}_k^T{\mathbf{q}}_j)\right).$

Since ${\mathbf{a}}_k^T{\mathbf{q}}_j={\mathbf{q}}_j^T{\mathbf{a}}_k$, we have:

${\mathbf{q}}_j^T{\mathbf{q}}_k=0.$

Thus, ${\mathbf{q}}_k$ is orthogonal to ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$.

3. ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_k$ span $S_k$:

By the inductive hypothesis, ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$ span $S_{k-1}$. The vector ${\mathbf{d}}_k$ is constructed as a linear combination of ${\mathbf{a}}_k$ and ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}$. Since ${\mathbf{a}}_k\in S_k$ and ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_{k-1}\subset S_{k-1}\subset S_k$, it follows that ${\mathbf{d}}_k\in S_k$. Hence, ${\mathbf{q}}_k\in S_k$.

Because ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_k$ are linearly independent and there are $k$ vectors in the $k$-dimensional space $S_k$, they form a basis for $S_k$.

Conclusion

The Gram-Schmidt process constructs an orthonormal basis ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_n$ for the span of the input vectors ${\mathbf{a}}_1,\dots ,{\mathbf{a}}_n$. By iteratively orthogonalizing and normalizing, it ensures that the resulting vectors are orthonormal and span the same subspace.

QR Decomposition

The Gram-Schmidt orthonormalization process naturally gives rise to a valuable matrix factorization called the QR decomposition. This decomposition expresses a matrix as the product of an orthogonal matrix (or a matrix with orthonormal columns) and an upper triangular matrix. It has significant applications in linear algebra computations, including solving least squares problems and finding eigenvalues.

Definition (QR Decomposition):

Let $A$ be an $m\times n$ matrix with linearly independent columns. The QR decomposition of $A$ is given by:
$A=QR,$
where:

• $Q$ is an $m\times n$ matrix with orthonormal columns (formed by the vectors ${\mathbf{q}}_1,\dots ,{\mathbf{q}}_n$ obtained from the Gram-Schmidt process applied to the columns of $A$), and
• $R$ is an $n\times n$ upper triangular matrix.

Lemma (Properties of QR Decomposition):

In the QR decomposition $A=QR$:

1. $R$ is upper triangular and invertible.
2. $Q{Q}^{T}A=A$. This shows that the columns of $Q$ span the same space as the columns of $A$, i.e., $C(Q)=C(A)$.

Proof of Properties:

1. Upper Triangularity of $R$:

The entries of $R$ are given by:
$r_{ij}={\mathbf{q}}_i^T{\mathbf{a}}_j.$

From the Gram-Schmidt process, ${\mathbf{q}}_i$ is orthogonal to ${\mathbf{a}}_1,\dots ,{\mathbf{a}}_{i-1}$ because ${\mathbf{q}}_i$ is orthogonal to the subspace spanned by ${\mathbf{a}}_1,\dots ,{\mathbf{a}}_{i-1}$. Therefore, for $i>j$:
$r_{ij}={\mathbf{q}}_i^T{\mathbf{a}}_j=0.$
This means $R$ is upper triangular.

2. Invertibility of $R$:

The matrix $R$ is constructed as an upper triangular matrix with diagonal entries $r_{ii}$ representing the norms of the orthogonal components ${\mathbf{d}}_i$ of the input vectors ${\mathbf{a}}_i$ (after subtracting projections onto the previously computed orthonormal vectors). Specifically:
$r_{ii}=\Vert {\mathbf{d}}_i\Vert ,$
where ${\mathbf{d}}_i={\mathbf{a}}_i-{\sum }_{j=1}^{i-1}({\mathbf{a}}_i^T{\mathbf{q}}_j){\mathbf{q}}_j$.

Key Reason for Non-Zero $r_{ii}$:

• The columns of $A$ are assumed to be linearly independent. This ensures that none of the input vectors ${\mathbf{a}}_i$ is in the span of the previous vectors ${\mathbf{a}}_1,\dots ,{\mathbf{a}}_{i-1}$. Consequently, after subtracting their projections, the resulting orthogonal component ${\mathbf{d}}_i$ is non-zero.
• Since $r_{ii}=\Vert {\mathbf{d}}_i\Vert$, and ${\mathbf{d}}_i\ne 0$, it follows that $r_{ii}\ne 0$ for all $i$.

Invertibility of $R$:

• $R$ is upper triangular by construction, with all diagonal entries $r_{ii}\ne 0$.
• A standard result in linear algebra is that an upper triangular matrix is invertible if and only if all its diagonal entries are non-zero.

3. $Q{Q}^{T}A=A$ and $C(Q)=C(A)$

We will rewrite the proof using the concept of projection matrices.

Step 1: Projection Matrix for $C(Q)$

The projection matrix onto the column space of $Q$, denoted as $P$, is given by:
$P=Q(Q^{T}Q{)}^{-1}{Q}^T.$ For matrices where $Q$ has orthonormal columns, we have $Q^{T}Q=I$, where $I$ is the identity matrix. Thus:
$P=Q(Q^{T}Q{)}^{-1}{Q}^T=Q{Q}^T.$

Step 2: Projection of $A$‘s Columns onto $C(Q)$

Let ${\mathbf{a}}_j$ denote the $j$-th column of $A$. Since $C(Q)=C(A)$ (i.e., the columns of $Q$ span the same space as the columns of $A$), the projection of ${\mathbf{a}}_j$ onto $C(Q)$ is the column itself. Formally:
${\text{proj}}_{C(Q)}({\mathbf{a}}_j)=P{\mathbf{a}}_j=Q{Q}^T{\mathbf{a}}_j.$

Since ${\mathbf{a}}_j\in C(Q)$, projecting ${\mathbf{a}}_j$ onto $C(Q)$ leaves it unchanged:
$Q{Q}^T{\mathbf{a}}_j={\mathbf{a}}_j.$

Step 3: Generalization to the Entire Matrix $A$

Applying the above argument to all columns of $A$, we see that the projection of $A$ onto $C(Q)$ is $A$ itself:
$Q{Q}^{T}A=A.$

Step 4: Why $C(Q)=C(A)$?

The equality $Q{Q}^{T}A=A$ implies that the columns of $Q$ span the same space as the columns of $A$. Specifically:

1. The action of $Q{Q}^T$ maps any vector in $C(A)$ to itself, ensuring that $C(Q)\supseteq C(A)$.
2. Since $Q$ is constructed using the Gram-Schmidt process on the columns of $A$, the columns of $Q$ are linear combinations of the columns of $A$, ensuring $C(Q)\subseteq C(A)$.

Therefore, $C(Q)=C(A)$, completing the proof.

Example of QR Decomposition

Let

We will compute its QR decomposition.

Step 1: Apply Gram-Schmidt to Columns of $A$

Let ${\mathbf{a}}_1=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]$ and ${\mathbf{a}}_2=\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]$.

1. Normalize ${\mathbf{a}}_1$:
   ${\mathbf{q}}_1=\frac{{\mathbf{a}}_1}{\Vert {\mathbf{a}}_1\Vert }=\frac{1}{\sqrt{3}}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right].$

2. Orthogonalize ${\mathbf{a}}_2$ relative to ${\mathbf{q}}_1$:
   The projection of ${\mathbf{a}}_2$ onto ${\mathbf{q}}_1$ is:
   ${\text{proj}}_{{\mathbf{q}}_1}({\mathbf{a}}_2)=({\mathbf{a}}_2^T{\mathbf{q}}_1){\mathbf{q}}_1=\left({\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]}^T\cdot \frac{1}{\sqrt{3}}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]\right)\cdot \frac{1}{\sqrt{3}}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right].$

   Compute the scalar $({\mathbf{a}}_2^T{\mathbf{q}}_1)$:
   ${\mathbf{a}}_2^T{\mathbf{q}}_1=\frac{1}{\sqrt{3}}(1\cdot 1+(-1)\cdot 1+1\cdot 1)=\frac{1}{\sqrt{3}}(1-1+1)=\frac{1}{\sqrt{3}}.$

   Therefore,
   ${\text{proj}}_{{\mathbf{q}}_1}({\mathbf{a}}_2)=\frac{1}{\sqrt{3}}\cdot \frac{1}{\sqrt{3}}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]=\frac{1}{3}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right].$

   Subtract this projection from ${\mathbf{a}}_2$ to get ${\mathbf{d}}_2$:
   ${\mathbf{d}}_2={\mathbf{a}}_2-{\text{proj}}_{{\mathbf{q}}_1}({\mathbf{a}}_2)=\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]-\frac{1}{3}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}1-\frac{1}{3}\\ -1-\frac{1}{3}\\ 1-\frac{1}{3}\end{array}\right]=\left[\begin{array}{c}\frac{2}{3}\\ -\frac{4}{3}\\ \frac{2}{3}\end{array}\right].$

3. Normalize ${\mathbf{d}}_2$:
   ${\mathbf{q}}_2=\frac{{\mathbf{d}}_2}{\Vert {\mathbf{d}}_2\Vert },$
   where:
   $\Vert {\mathbf{d}}_2\Vert =\sqrt{{\left(\frac{2}{3}\right)}^2+{\left(-\frac{4}{3}\right)}^2+{\left(\frac{2}{3}\right)}^2}=\sqrt{\frac{4}{9}+\frac{16}{9}+\frac{4}{9}}=\sqrt{\frac{24}{9}}=\sqrt{\frac{8}{3}}=\frac{2\sqrt{6}}{3}.$

   Thus:
   ${\mathbf{q}}_2=\frac{\left[\begin{array}{c}\frac{2}{3}\\ -\frac{4}{3}\\ \frac{2}{3}\end{array}\right]}{\frac{2\sqrt{6}}{3}}=\frac{1}{\sqrt{6}}\left[\begin{array}{c}1\\ -2\\ 1\end{array}\right].$

Step 2: Construct $Q$ and $R$

The orthonormal vectors ${\mathbf{q}}_1$ and ${\mathbf{q}}_2$ form the columns of $Q$:

The matrix $R$ is given by $R=Q^{T}A$:

1. Compute $r_{11}$:
   $r_{11}=\Vert {\mathbf{a}}_1\Vert =\sqrt{1^2+1^2+1^2}=\sqrt{3}.$

2. Compute $r_{12}$:
   $r_{12}={\mathbf{q}}_1^T{\mathbf{a}}_2=\frac{1}{\sqrt{3}}{\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]}^T\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]=\frac{1}{\sqrt{3}}(1-1+1)=\frac{1}{\sqrt{3}}.$

3. Compute $r_{22}$:
   $r_{22}=\Vert {\mathbf{d}}_2\Vert =\frac{2\sqrt{6}}{3}.$

The matrix $R$ is:

Final QR Decomposition

Computational Usefulness of QR Decomposition

1. Projections:

Since $C(A)=C(Q)$, projecting onto $C(A)$ is the same as projecting onto $C(Q)$. With orthonormal columns in $Q$, the projection simplifies to:
${\text{proj}}_{C(A)}(\mathbf{b})=Q{Q}^T\mathbf{b}.$

2. Least Squares:

The least squares solution to $A\mathbf{x}=\mathbf{b}$ minimizes $\Vert A\mathbf{x}-\mathbf{b}{\Vert }^2$. Using the QR decomposition ($A=QR$), the normal equations $A^{T}A\mathbf{x}=A^T\mathbf{b}$ become:
$R^{T}R\mathbf{x}=R^T{Q}^T\mathbf{b}.$

Since $R$ is invertible, this simplifies to:
$R\mathbf{x}=Q^T\mathbf{b},$
which can be efficiently solved by back-substitution because $R$ is upper triangular.

Continue here: 20 Pseudoinverses, Constructing Pseudoinverses