19 Factorizations, Polynomial Fields and Division, Polynomial Interpolation, Constructing Galois Fields

Lecture from: 20.11.2024 | Video: Videos ETHZ

Interesting Factorization in Rings

Factorization in a ring $R$ becomes more interesting when not every element is a unit (i.e., has a multiplicative inverse). If every non-zero element is a unit, as in the field $\mathbb{R}$ of real numbers, any element can be trivially factored. For example, $\pi =\pi \cdot 1=\frac{\pi }{\sqrt{2}}\cdot \sqrt{2}$. These factorizations aren’t particularly insightful because we’re just multiplying by units.

For factorization to be meaningful, we want the group of units $R^{\ast }$ to be significantly smaller than the ring itself: $|R^{\ast }|\ll |R|$.

Non-Trivial Factorization: Let’s define a non-trivial factorization as $a=b\cdot c$, where $a,b,c\in R$ and $b,c\notin R^{\ast }$. This ensures that neither $b$ nor $c$ are simply units being multiplied by $a$. In fields like $\mathbb{R}$, there are no non-trivial factorizations.

Integers: The ring of integers $\mathbb{Z}$ offers interesting factorizations because its units are only $\{1,-1\}$. For example, $10=2\cdot 5$ is a non-trivial factorization.

Factorization in Gaussian Integers

Consider the Gaussian integers $\mathbb{Z}[i]$, complex numbers of the form $a+bi$ where $a$ and $b$ are integers. Let’s factorize $1+3i$.

1. Using the Norm: The norm of a Gaussian integer $a+bi$ is defined as $N(a+bi)=a^2+b^2$. The norm is multiplicative: $N((a+bi)(c+di))=N(a+bi)N(c+di)$.

2. Norm of $1+3i$: $N(1+3i)=1^2+3^2=10$.

3. Factoring the Norm: $10=2\cdot 5$. If $1+3i$ can be factored, the norms of the factors must multiply to 10.

4. Potential Factors: We look for Gaussian integers with norms 2 and 5. $1+i$ has norm 2, and $2+i$ has norm 5.

5. Factorization: Indeed, $(1+i)(2+i)=(2+i+2i+i^2)=(2-1+3i)=1+3i$.

6. Irreducible Factors: $1+i$ and $2+i$ are irreducible in $\mathbb{Z}[i]$. This is because their norms are prime integers, and any further factorization would require Gaussian integers with norms that are not integers, which is impossible.

Units and Associates: Notice that if you find an irreducible element like $2+i$, you can multiply it by any unit ($1,-1,i,-i$) to get another irreducible element. These are called associates. For example, $i(2+i)=-1+2i$, $-(2+i)=-2-i$, and $-i(2+i)=1-2i$ are also irreducible. Each irreducible Gaussian integer is thus one of four associates.

Gaussian Primes

Visualizing Irreducible Gaussian Integers: Plotting the Gaussian integers and highlighting the irreducible ones reveals an interesting pattern related to prime numbers and sums of squares.

Zoomed Out:

Link: https://www.alpertron.com.ar/GAUSSPR.HTM

Gaussian Integers Modulo an Irreducible Element

We’ll use the example of $m=2+i$, which is irreducible in $\mathbb{Z}[i]$. We’re forming the quotient ring $\mathbb{Z}[i{]}_{2+i}=\mathbb{Z}[i]/(2+i)$, which consists of equivalence classes of Gaussian integers modulo $2+i$.

1. Elements within the Circle: If we consider the Gaussian integers strictly within a circle of radius $|2+i|=\sqrt{5}$ centered at the origin, we find 13 such elements.

   

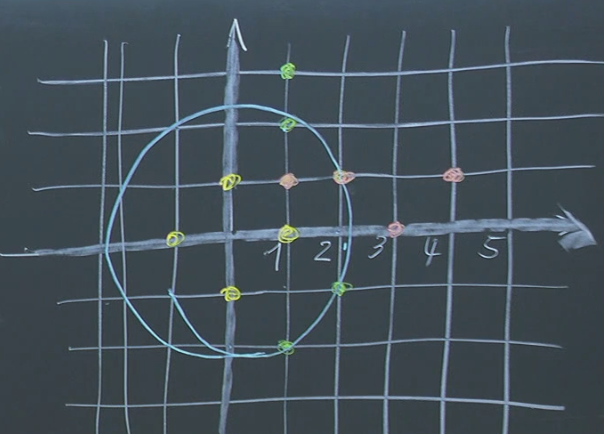
   These are: $0,1,2,-1,-2,i,2i,-i,-2i,1+i,1-i,-1+i,-1-i$.

Lecturer's Mistake

In my opinion, in the lecture, it was mistakenly stated that there are 13 distinct elements in the field $\mathbb{Z}[i{]}_{2+i}$. This is incorrect. While there are 13 Gaussian integers within the circle of radius $\sqrt{5}$, many of them are equivalent modulo $2+i$.

2. Modular Equivalence: In the “mod $2+i$ world,” many of these 13 elements are equivalent. Two Gaussian integers $z$ and $w$ are equivalent modulo $2+i$ if their difference is a multiple of $2+i$: $z\equiv w(\mathrm{mod}2+i)$ if $z-w=k(2+i)$ for some Gaussian integer $k$.

   • Example 1: $2\equiv -i(\mathrm{mod}2+i)$ because $2-(-i)=2+i$, which is a multiple of $2+i$.
   • Example 2: $1+i\equiv -1(\mathrm{mod}2+i)$ because $(1+i)-(-1)=2+i$.

3. Distinct Representatives: When we account for these equivalences, we find only five distinct equivalence classes (or cosets) in $\mathbb{Z}[i{]}_{2+i}$. A convenient set of representatives for these classes is $\{0,1,-1,i,-i\}$. Every Gaussian integer is congruent modulo $2+i$ to precisely one of these five representatives.

4. Field Structure: $\mathbb{Z}[i{]}_{2+i}$ forms a field with five elements. As all finite fields with the same number of elements are isomorphic, $\mathbb{Z}[i{]}_{2+i}$ is isomorphic to ${\mathbb{Z}}_5$ (or $GF(5)$). The modulo $2+i$ construction gives us an alternative way to represent this finite field.

Polynomial Fields and Euclidean Division

In polynomial rings $F[x]$, where $F$ is a field, we can perform polynomial long division, much like integer division. This leads to the concept of a residue polynomial and modular arithmetic with polynomials.

Euclidean Division: For any two polynomials $a(x)$ and $m(x)$ in $F[x]$ (with $m(x)\ne 0$), there exist unique polynomials $q(x)$ (quotient) and $r(x)$ (remainder) in $F[x]$ such that:

$a(x)=m(x)\cdot q(x)+r(x)$, where $\text{deg}(r(x))<\text{deg}(m(x))$ or $r(x)=0$.

Modular Congruence: Just as with integers, we can define modular congruence for polynomials. We say that $a(x)$ is congruent to $r(x)$ modulo $m(x)$, written as:

$a(x){\equiv }_{m(x)}r(x)$ or $a(x)\equiv r(x)(\mathrm{mod}m(x))$

This means $a(x)$ and $r(x)$ have the same remainder when divided by $m(x)$. We can also express the remainder using the notation:

$R_{m(x)}(a(x))=r(x)$

Example: $\mathbb{R}[x]$

Let’s divide $a(x)=5x^3-2x+1$ by $m(x)=3x^2+2$ in $\mathbb{R}[x]$:

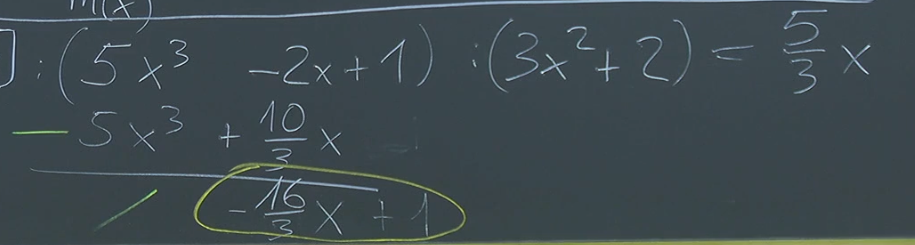
Here, the quotient is $q(x)=\frac{5}{3}x$ and the remainder is $r(x)=-\frac{16}{3}x+1$. Notice that $\text{deg}(r(x))=1<\text{deg}(m(x))=2$.

Thus, we can write:

$5x^3-2x+1=(3x^2+2)(\frac{5}{3}x)+(-\frac{16}{3}x+1)$

And in modular notation:

$5x^3-2x+1\equiv -\frac{16}{3}x+1(\mathrm{mod}3x^2+2)$

This Euclidean division and the resulting modular arithmetic are fundamental tools for working with polynomial rings and constructing extension fields.

Polynomials as Functions

While we can represent polynomials in $F[x]$ as sequences of coefficients, it’s often beneficial to view them as functions from $F$ to $F$. This perspective allows for a deeper understanding of polynomial properties and enables applications like polynomial interpolation and error-correcting codes.

Recall that in $F[x]$, addition and multiplication are defined in the natural way:

• Addition: $a(x)+b(x)=(a+b)(x)$, where the coefficients are added term-wise.
• Multiplication: $a(x)\cdot b(x)=c(x)$, where $c(x)$ is obtained through polynomial multiplication.

Example: $GF(5)[x]$

Consider the polynomial $a(x)=2x^3+3x+1$ in $GF(5)[x]$. Here, the coefficients and the variable $x$ take values in $GF(5)=\{0,1,2,3,4\}$.

We can evaluate $a(x)$ at each element of $GF(5)$:

• $a(0)=2(0{)}^3+3(0)+1=1$
• $a(1)=2(1{)}^3+3(1)+1=2+3+1=6\equiv 1(\mathrm{mod}5)$
• $a(2)=2(2{)}^3+3(2)+1=16+6+1=23\equiv 3(\mathrm{mod}5)$
• $a(3)=2(3{)}^3+3(3)+1=54+9+1=64\equiv 4(\mathrm{mod}5)$
• $a(4)=2(4{)}^3+3(4)+1=128+12+1=141\equiv 1(\mathrm{mod}5)$

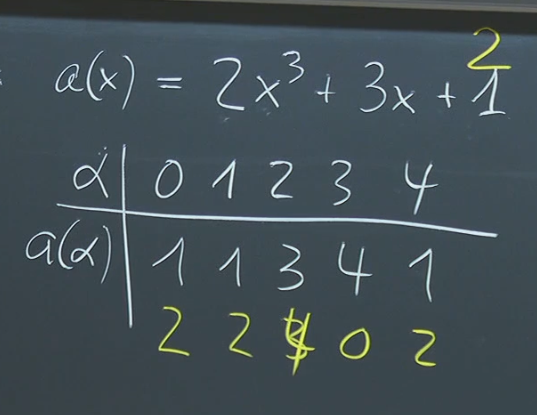
As we can see, some polynomials have roots (values where the polynomial evaluates to zero) within the field, while others do not. $a(x)$ does not have a root in $GF(5)$.

Lemma 5.29: The Factor Theorem

A key connection between roots and factors of a polynomial is captured by the Factor Theorem:

Lemma 5.29 (Factor Theorem)

Let $F$ be a field, $\alpha \in F$, and $a(x)\in F[x]$. Then $(x-\alpha )$ divides $a(x)$ if and only if $a(\alpha )=0$.

Proof:

($\Rightarrow$) If $(x-\alpha )$ divides $a(x)$, then $a(x)=(x-\alpha )q(x)$ for some polynomial $q(x)\in F[x]$. Substituting $x=\alpha$, we get $a(\alpha )=(\alpha -\alpha )q(\alpha )=0\cdot q(\alpha )=0$.

($\Leftarrow$) If $a(\alpha )=0$, we can use the division algorithm for polynomials. We can divide $a(x)$ by $(x-\alpha )$ to get a quotient $q(x)$ and a remainder $r(x)$, where the degree of $r(x)$ is less than the degree of $(x-\alpha )$. So $r(x)$ is a constant, say $r\in F$.

Thus, $a(x)=(x-\alpha )q(x)+r$. Substituting $x=\alpha$, we get $a(\alpha )=(\alpha -\alpha )q(\alpha )+r=r$. Since $a(\alpha )=0$, we have $r=0$. Therefore, $a(x)=(x-\alpha )q(x)$, which means $(x-\alpha )$ divides $a(x)$.

This lemma is fundamental for relating the roots of a polynomial to its factorization.

Polynomial Interpolation

Polynomial interpolation is the process of finding a polynomial that passes through a given set of points. Given $n+1$ data points $(x_0,y_0),(x_1,y_1),\dots ,(x_n,y_n)$, where the $x_i$ are distinct, there exists a unique polynomial $a(x)$ of degree at most $n$ such that $a(x_i)=y_i$ for all $i$.

Example in $GF(5)[x]$

Let’s work in $GF(5)[x]$, the ring of polynomials with coefficients in the finite field $GF(5)$. We want to find a polynomial $a(x)$ of degree at most 2 (i.e., $a(x)=a_2{x}^2+a_{1}x+a_0$) such that $a(1)=2$, $a(3)=1$, and $a(4)=4$.

We can set up a system of linear equations:

• $a(1)=a_2+a_1+a_0\equiv 2(\mathrm{mod}5)$
• $a(3)=9a_2+3a_1+a_0\equiv 4a_2+3a_1+a_0\equiv 1(\mathrm{mod}5)$
• $a(4)=16a_2+4a_1+a_0\equiv a_2+4a_1+a_0\equiv 4(\mathrm{mod}5)$

This gives us the system of congruences:

• $a_2+a_1+a_0\equiv 2(\mathrm{mod}5)$
• $4a_2+3a_1+a_0\equiv 1(\mathrm{mod}5)$
• $a_2+4a_1+a_0\equiv 4(\mathrm{mod}5)$

This system can be solved using Gaussian elimination (as discussed in 08 Gauss Elimination, Elimination Matrices and Solution Sets).

If the $y_i$ values come from evaluating a polynomial of degree at most $n$ at the $x_i$ values, the resulting matrix will be invertible. This guarantees a unique solution for the coefficients $a_0,a_1,a_2$. Since our $x_i$ values are distinct in $GF(5)$ and $a(x)$ has degree at most 2, the given information should allow for reconstruction.

General Rule

To interpolate a polynomial of degree at most $n$, we need $n+1$ data points. This can be understood from a linear algebra perspective. We have $n+1$ unknown coefficients ($a_0,a_1,\dots ,a_n$) and $n+1$ equations (one for each data point). This creates a square $(n+1)\times (n+1)$ matrix. If the $x_i$ values are distinct, the matrix is invertible, guaranteeing a unique solution for the coefficients.

For more see: Vandermonde Matrices

Lagrange Interpolation

Lagrange interpolation provides an explicit formula for the interpolating polynomial. Given $d+1$ data points $({\alpha }_1,{\beta }_1),({\alpha }_2,{\beta }_2),\dots ,({\alpha }_{d+1},{\beta }_{d+1})$, where the ${\alpha }_i$ are distinct elements of a field $F$, we want to find a polynomial $a(x)\in F[x]$ of degree at most $d$ such that $a({\alpha }_i)={\beta }_i$ for all $i=1,2,\dots ,d+1$.

The idea behind Lagrange interpolation is to construct a set of basis polynomials $u_i(x)$ with the following property:

$u_i({\alpha }_j)=\{\begin{array}{ll}1,& \text{if }i=j\\ 0,& \text{if }i\ne j\end{array}$

These $u_i(x)$ polynomials act like “switches,” turning on (evaluating to 1) only at their corresponding ${\alpha }_i$ and turning off (evaluating to 0) at all other ${\alpha }_j$.

Once we have these basis polynomials, the interpolating polynomial $a(x)$ can be constructed as a linear combination:

$a(x)={\sum }_{i=1}^{d+1}{\beta }_i{u}_i(x)$

This works because when we evaluate $a(x)$ at ${\alpha }_j$:

$a({\alpha }_j)={\sum }_{i=1}^{d+1}{\beta }_i{u}_i({\alpha }_j)={\beta }_j{u}_j({\alpha }_j)={\beta }_j$

since all other terms $u_i({\alpha }_j)$ where $i\ne j$ are zero.

The Lagrange basis polynomials are defined as:

$u_i(x)={\prod }_{\begin{array}{c}1\le j\le d+1\\ j\ne i\end{array}}\frac{x-{\alpha }_j}{{\alpha }_i-{\alpha }_j}$

In other notation, the Lagrange basis polynomial $u_i(x)$ is defined as:

$u_i(x)=\frac{(x-{\alpha }_1)}{{\alpha }_i-{\alpha }_1}\cdot \frac{(x-{\alpha }_2)}{{\alpha }_i-{\alpha }_2}\cdots \frac{(x-{\alpha }_{i-1})}{{\alpha }_i-{\alpha }_{i-1}}\cdot \frac{(x-{\alpha }_{i+1})}{{\alpha }_i-{\alpha }_{i+1}}\cdots \frac{(x-{\alpha }_{d+1})}{{\alpha }_i-{\alpha }_{d+1}}$

Note that the term $\frac{(x-{\alpha }_i)}{{\alpha }_i-{\alpha }_i}$ is omitted from the product. This is explicitly stated in the original notation with $j\ne i$ under the product symbol.

Each $u_i(x)$ is a polynomial of degree $d$. It’s constructed to be 1 at $x={\alpha }_i$ and 0 at all other $x={\alpha }_j$ where $j\ne i$.

This formula ensures that $u_i({\alpha }_i)=1$ (because the factors in the numerator and denominator become the same) and $u_i({\alpha }_j)=0$ for $j\ne i$ (because the factor $x-{\alpha }_j$ becomes zero in the numerator).

Lagrange interpolation thus provides a direct and elegant way to construct the interpolating polynomial, although for large $d$, evaluating this formula can become computationally expensive.

Theorem 5.31: A Non-Zero Polynomial of Degree $d$ Has at Most $d$ Roots in a Field

Let $F$ be a field. A non-zero polynomial $f(x)\in F[x]$ of degree $d$ has at most $d$ roots in $F$.

Proof:

1. Distinct Roots: Let ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_e$ be distinct roots of $f(x)$ in $F$. This means $f({\alpha }_i)=0$ for each $i=1,2,\dots ,e$.

2. Factorization: By the Factor Theorem (Lemma 5.29), if $\alpha$ is a root of $f(x)$ in $F$, then $(x-\alpha )$ is a factor of $f(x)$. Therefore, for each distinct root ${\alpha }_i$, we have $(x-{\alpha }_i)|f(x)$.

3. Product of Factors: We can combine the distinct linear factors corresponding to the distinct roots into a single factor: ${\prod }_{i=1}^e(x-{\alpha }_i)|f(x)$.

4. Degree Comparison: The degree of the product ${\prod }_{i=1}^e(x-{\alpha }_i)$ is $e$. Since $f(x)$ has degree $d$, and the degree of a product of polynomials is the sum of their degrees, we must have $e\le d$.

5. Conclusion: Thus, $f(x)$ has at most $d$ distinct roots in $F$.

Note

This theorem holds only for non-zero polynomials. The zero polynomial has infinitely many roots. Also note that the degree of the polynomial must be exactly equal to $d$. Otherwise the amount of roots can only be less than d and never equal to $d$, because the factored-out linear factors already decrease the total possible roots.

Proving Uniqueness of the Interpolated Polynomial

Now, let’s prove the uniqueness of the interpolated polynomial.

1. Assumption: Suppose we have two different polynomials $a(x)$ and $a^{\prime }(x)$, both of degree at most $d$, that interpolate the same $d+1$ data points $({\alpha }_1,{\beta }_1),\dots ,({\alpha }_{d+1},{\beta }_{d+1})$. This means $a({\alpha }_i)=a^{\prime }({\alpha }_i)={\beta }_i$ for all $i=1,2,\dots ,d+1$.

2. Difference Polynomial: Consider the polynomial $b(x)=a(x)-a^{\prime }(x)$. Since $a(x)$ and $a^{\prime }(x)$ have degree at most $d$, $b(x)$ also has degree at most $d$.

3. Roots of b(x): For each ${\alpha }_i$, we have $b({\alpha }_i)=a({\alpha }_i)-a^{\prime }({\alpha }_i)={\beta }_i-{\beta }_i=0$. This means $b(x)$ has at least $d+1$ distinct roots (${\alpha }_1,\dots ,{\alpha }_{d+1}$).

4. Contradiction: We have a non-zero polynomial $b(x)$ of degree at most $d$ with $d+1$ distinct roots. This contradicts the theorem we just proved.

5. Conclusion: Therefore, our initial assumption must be false. There cannot be two different interpolating polynomials of degree at most $d$ for the same $d+1$ data points. The interpolated polynomial is unique.

Constructing Galois Fields using Polynomials

We can construct finite fields using polynomial rings. The process involves creating a quotient ring of polynomials modulo an irreducible polynomial.

1. Start with a Finite Field: Begin with a finite field $F$ (e.g., ${\mathbb{Z}}_p$ where $p$ is prime). Let $|F|=q$. In many cases this is just a prime $p$, meaning $|F|=p$.

2. Polynomial Ring: Consider the polynomial ring $F[x]$, which consists of polynomials with coefficients in $F$.

3. Irreducible Polynomial: Choose an irreducible polynomial $m(x)\in F[x]$ of degree $d$. An irreducible polynomial is one that cannot be factored into lower-degree polynomials within $F[x]$.

4. Quotient Ring (Finite Field): Construct the quotient ring $F[x{]}_{m(x)}=F[x]/(m(x))$. This consists of the equivalence classes of polynomials in $F[x]$ modulo $m(x)$. Two polynomials are equivalent if they have the same remainder when divided by $m(x)$.

Representing Elements

The elements of $F[x{]}_{m(x)}$ can be uniquely represented by polynomials of degree less than $d$. This is because any polynomial $a(x)\in F[x]$ can be written as $a(x)=q(x)m(x)+r(x)$, where $r(x)$ is the remainder and $\text{deg}(r(x))<\text{deg}(m(x))=d$. The remainder $r(x)$ serves as the representative of the equivalence class.

5. Size of the Field: Because elements are represented by polynomials of degree less than $d$, and each of the $d$ coefficients can be any of the $q$ elements of $F$, the size of the quotient ring (and thus the field) is $|F[x{]}_{m(x)}|=q^d=|F{|}^d$.

6. Field Operations:

   • Addition: Addition is performed component-wise on the coefficients of the polynomials, modulo the characteristic of the field $F$. That is, each coefficient is the sum of the corresponding coefficients in ${\mathbb{Z}}_p$, so the coefficient of $x^i$ of the sum of two polynomials is the sum of their coefficients of $x^i$ modulo $p$. The resulting polynomial has also a degree less than $d$.

   • Multiplication: Multiplication is performed by multiplying the polynomials as usual and then taking the remainder when dividing by $m(x)$. Since $m(x)$ has degree $d$, this ensures the result can also be represented by a polynomial of degree less than $d$.

Example: Constructing $GF(8)=GF(2^3)={\mathbb{Z}}_2[x{]}_{x^3+x+1}$

Let $F={\mathbb{Z}}_2=\{0,1\}$ and let $m(x)=x^3+x+1$. The polynomial $m(x)$ is irreducible in ${\mathbb{Z}}_2[x]$ because it has no roots in ${\mathbb{Z}}_2$. Thus $GF(8)={\mathbb{Z}}_2[x]/(x^3+x+1)=\{0,1,x,x+1,x^2,x^2+1,x^2+x,x^2+x+1\}$. Here $|GF(8)|=2^3=8$.

Let’s multiply $x^2+1$ and $x+1$:

$(x^2+1)(x+1)=x^3+x^2+x+1$

Now we divide this by $m(x)=x^3+x+1$:

$(x^3+x^2+x+1)=1(x^3+x+1)+x^2$

The remainder is $x^2$. Thus: $(x^2+1)(x+1)=x^2$ in ${\mathbb{Z}}_2[x{]}_{x^3+x+1}$.

This method allows us to construct finite fields of any prime power order $q^d$. These fields are crucial in various areas like cryptography and coding theory. The irreducibility of $m(x)$ guarantees the existence of multiplicative inverses for all non-zero elements in the quotient ring, fulfilling the requirements of a field.

Modular Arithmetic and Polynomial GCDs

The concept of modular arithmetic with integers extends naturally to polynomials. Recall that for integers $a$, $b$, and $m$, the equation $ab\equiv 1(\mathrm{mod}m)$ has a solution (meaning $a$ has a multiplicative inverse modulo $m$) if and only if $\text{gcd}(a,m)=1$. This is based on the ideal structure of integers.

Ideals and GCDs:

For integers $a$ and $m$, the ideal generated by $a$ and $m$ is denoted $(a,m)=\{ax+my\mid x,y\in \mathbb{Z}\}$. A fundamental result in number theory states that this ideal is principal, meaning it can be generated by a single element.

Proof that $(d)⟹d=\text{gcd}(a,m)$ (up to units)

Assume $(a,m)=(d)$. This means:

1. $d$ can be written as a linear combination of $a$ and $m$: $d=ax+my$ for some integers $x$ and $y$.
2. Since $a\in (d)$ and $m\in (d)$, there exist integers $k$ and $l$ such that $a=kd$ and $m=ld$. This follows directly from the definition of the ideal $(d)=\{nd\mid n\in \mathbb{Z}\}$. Because $a$ and $m$ can be expressed as multiples of $d$, this shows that $d$ is a common divisor of $a$ and $m$.
3. Let $c$ be any common divisor of $a$ and $m$. This means $a=nc$ and $m=n^{\prime }c$ for some integers $n$ and $n^{\prime }$. Substituting into the equation $d=ax+my$, we have $d=(nc)x+(n^{\prime }c)y=c(nx+n^{\prime }y)$. Therefore, $d$ is a multiple of $c$, which implies that $d$ is the greatest common divisor (since any other common divisor $c$ divides $d$).

In rings with units (invertible elements), $d$ is equal to the gcd up to multiplication by a unit. So, $d=u\cdot \text{gcd}(a,m)$, where $u$ is a unit. In $\mathbb{Z}$, the units are $1$ and $-1$, so $d=\pm \text{gcd}(a,m)$.

Polynomial Analogy:

This concept translates directly to polynomials. Let $a(x)$ and $m(x)$ be polynomials in a field $F[x]$. The ideal generated by $a(x)$ and $m(x)$ is $(a(x),m(x))=\{a(x)u(x)+m(x)v(x)\mid u(x),v(x)\in F[x]\}$. Similar to integers, this ideal is principal: $(a(x),m(x))=(d(x))$, where $d(x)=\text{gcd}(a(x),m(x))$ (up to multiplication by units in $F[x]$, which are non-zero constant polynomials).

Multiplicative Inverses for Polynomials:

The equation $a(x)b(x)\equiv 1(\mathrm{mod}m(x))$ has a solution $b(x)$ (i.e., $a(x)$ has a multiplicative inverse modulo $m(x)$) if and only if $\text{gcd}(a(x),m(x))=1$.

Proof of the Condition for Polynomial Inverses

1. If $\text{gcd}(a(x),m(x))=1$: There exist polynomials $u(x)$ and $v(x)$ such that $a(x)u(x)+m(x)v(x)=1$. Modulo $m(x)$, this becomes $a(x)u(x)\equiv 1(\mathrm{mod}m(x))$, making $u(x)$ the inverse of $a(x)$.
2. If $a(x)b(x)\equiv 1(\mathrm{mod}m(x))$: Then $a(x)b(x)=1+m(x)k(x)$ for some $k(x)$. So, $a(x)b(x)-m(x)k(x)=1$. Any common divisor of $a(x)$ and $m(x)$ must divide 1, implying the gcd is 1.

Note that $\text{gcd}(a(x),m(x))=1$ for any non-zero $a(x)$ with degree less than $m(x)$ when $m(x)$ is irreducible. This is because an irreducible polynomial cannot share any non-trivial factors with a lower-degree polynomial. If the $\text{gcd}(a(x),m(x))$ were not 1, it would imply that $m(x)$ is divisible by some polynomial, which contradicts its irreducibility unless $a(x)$ is a unit (a constant). Since we consider $a(x)$ to have a lower degree than $m(x)$ and since $a(x)\ne 0$, the gcd must be 1.

Conclusion:

The existence of multiplicative inverses for polynomials modulo another polynomial hinges on their greatest common divisor, mirroring the situation with integers. This is fundamental for constructing finite fields from polynomial rings. When $m(x)$ is irreducible, all non-zero polynomials $a(x)$ with $\text{deg}(a(x))<\text{deg}(m(x))$ have inverses modulo $m(x)$. This is what makes $F[x{]}_{m(x)}$ a field.

These fields are also called Galois Fields and are usually denoted as $GF(q^d)$, where $q=|F|$ (the size of the base field $F$) and $d$ is the degree of the irreducible polynomial $m(x)$. $GF(q^d)$ contains $q^d$ elements. Specifically ${\mathbb{Z}}_p[x{]}_{m(x)}$ is denoted as $GF(p^d)$ with $|GF(p^d)|=p^d$.

Example: $\mathbb{R}[x{]}_{x^2+1}$

The quotient ring $\mathbb{R}[x{]}_{x^2+1}$ is isomorphic to the field of complex numbers, $\mathbb{C}$. Elements $ax+b$ in $\mathbb{R}[x{]}_{x^2+1}$ correspond to $a+bi$ in $\mathbb{C}$, with $x$ playing the role of $i$. Addition is component-wise, and multiplication modulo $x^2+1$ mirrors complex multiplication: $(ax+b)(cx+d)\equiv (ad+bc)x+(bd-ac)$, analogous to $(a+bi)(c+di)=(bc+ad)i+(bd-ac)$.

Continue here: 20 Generators in Finite Fields, Properties of Finite Fields, Error Correcting Codes, Reed-Solomon Codes